Взаимодействия среды

expand чувствителен к свойствам набора идентификаторов через assume.

Пример 1

expand расширяет продукты сумм путем умножения:

expand((x + 1)*(y + z)^2)

После расширения числителя часть переписана как сумма частей:

expand((x + 1)^2*y/(y + z)^2)

Пример 2

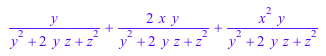
Степень с суммой в экспоненте переписана как продукт степеней:

expand(x^(y + z + 2))

Пример 3

expand работает рекурсивным способом. В следующем примере степень (x + y) ^{z + 2} сначала расширен в продукт двух степеней. Затем степень (x + y) ² расширена в сумму. Наконец, продукт последней суммы и остающейся степени (x + y) ^z умножается:

expand((x + y)^(z + 2))

Вот другой пример:

expand(2^((x + y)^2))

expand сопоставляет на записях списков, наборов и матриц:

expand([(a + b)^2, (a - b)^2]);
expand({(a + b)^2, (a - b)^2});
expand(matrix([[(a + b)^2, 0],[0, (a - b)^2]]))

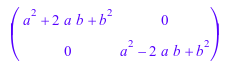
expand не сопоставляет на записях таблиц или массивов:

expand(table((a + b)^2=(c + 1)^2)),
expand(array(1..1, [(a + b)^2]))

Используйте map в порядке расширить все записи контейнера:

map(table((a + b)^2=(c + 1)^2), expand),
map(array(1..1, [(a + b)^2]), expand)

Обратите внимание на то, что этот вызов расширяет только записи в таблице, не ключи. В (редком) случае, что вы хотите ключи, расширенные также, преобразуйте таблицу к списку или системе уравнений сначала:

T := table((a + b)^2=(c + 1)^2):
table(expand([op(T)]))

Пример 4

Если дополнительные аргументы обеспечиваются, expand выполняет только частичное расширение. Эти дополнительные выражения, такие как x + 1 в следующем примере, не расширены:

expand((x + 1)*(y + z))

expand((x + 1)*(y + z), x + 1)

Пример 5

По умолчанию expand работает над всеми подвыражениями включая тригонометрические подвыражения:

e := (sin(2*x) + 1)*(1 - cos(2*x)):
expand(e)

Чтобы предотвратить расширение подвыражений, используйте опцию ArithmeticOnly:

expand(e, ArithmeticOnly)

Опция не предотвращает расширение степеней и корней:

expand((sin(2*x) + 1)^3, ArithmeticOnly)

Чтобы сохранить подвыражения с целочисленными степенями нерасширенными, используйте опцию MaxExponent.

Пример 6

Опция IgnoreAnalyticConstraints применяет набор чисто алгебраических упрощений включая равенство суммы логарифмов и логарифма продукта. Используя опцию IgnoreAnalyticConstraints, вы получаете более простой результат, но тот, который может быть неправильным для некоторых значений переменных:

expand(ln(a*b*c*d), IgnoreAnalyticConstraints)

Не используя эту опцию, вы получаете математически правильный результат:

expand(ln(a*b*c*d))

Пример 7

Если дополнительный MaxExponent, если, expand выполняет только частичное расширение. Полномочия с целочисленной экспонентой, больше, чем связанный данный, не расширены:

expand((a + b)^3, MaxExponent = 2)

Если экспонента меньше, или равняйтесь связанному данному, степень расширена:

expand((a + b)^2, MaxExponent = 2)

Пример 8

Функция expand может принять несколько опций одновременно. Предположим, что вы хотите расширить следующее выражение:

e := (sin(2*x) + 1)*(x + 1)^3

expand без любых опций работает рекурсивно. Функция расширяет все подвыражения включая тригонометрические функции и степени:

expand(e)

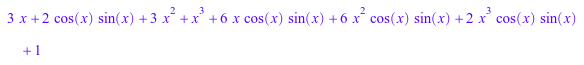
Опция ArithmeticOnly предотвращает расширение термина sin(2x). Опция MaxExponent предотвращает расширение (x + 1) ³:

expand(e, ArithmeticOnly);
expand(e, MaxExponent = 2)

Комбинируя эти опции в одном вызове функции expand, вы вводите оба ограничения для расширения:

expand(e, MaxExponent = 2, ArithmeticOnly)

Пример 9

Следующие расширения не допустимы для всех значений a, b от комплексной плоскости. Therefore, MuPAD^® не расширяет эти выражения:

expand(ln(a^2)), expand(ln(a*b)), expand((a*b)^n)

Расширения допустимы под предположением, что a является положительным вещественным числом:

assume(a > 0):  expand(ln(a^2)), expand(ln(a*b)), expand((a*b)^n)

Очистите предположение для дальнейших вычислений:

unassume(a):

Также, чтобы получить расширенный результат для третьего выражения, примите, что n является целым числом:

expand((a*b)^n) assuming n in Z_

Используйте опцию IgnoreAnalyticConstraints, чтобы расширить эти выражения без явным образом заданных предположений:

expand(ln(a^2), IgnoreAnalyticConstraints),
expand(ln(a*b), IgnoreAnalyticConstraints),
expand((a*b)^n, IgnoreAnalyticConstraints)

Пример 10

Теоремы сложения тригонометрии реализованы "expand" - слоты тригонометрических функций sin и cos:

expand(sin(a + b)), expand(sin(2*a))

То же самое верно для гиперболических функций sinh и cosh:

expand(cosh(a + b)), expand(cosh(2*a))

Показательная функция с суммой в качестве аргумента расширена через exp::expand:

expand(exp(a + b))

Вот являются еще некоторые примеры расширения для функций sum, fact, abs, coth, sign, binomial, beta, gamma, cot, tan, exp и psi:

sum(f(x) + g(x),x);  expand(%)

fact(x + 1);  expand(%)

abs(a*b);  expand(%)

coth(a + b);  expand(%)

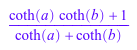
coth(a*b);  expand(%)

sign(a*b);  expand(%)

binomial(n, m);  expand(%)

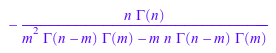
beta(n, m);  expand(%)

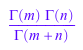
gamma(x + 1);  expand(%)

tan(a + b); expand(%)

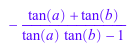
cot(a + b); expand(%)

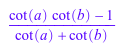
exp(x + y);  expand(%)

psi(x + 2);  expand(%)

В отличие от предыдущих версий MuPAD, expand не переписывает tan с точки зрения sin и cos:

expand(tan(a))

Пример 11

Этот пример иллюстрирует, как расширить функциональность expand к пользовательским математическим функциям. Как пример, мы рассматриваем синусоидальную функцию. (Конечно, системная функция sin уже имеет слот "expand"; смотрите Пример 10.)

Мы сначала встраиваем нашу функцию в функциональную среду, которая мы вызываем Sin, по порядку чтобы не перезаписать системную функцию sin. Затем мы реализуем теорему сложения sin (x + y) = sin (x)  cos (y) + sin (y)  cos (x) в слоте "expand" функциональной среды, т.е. стандартная программа слота Sin::expand:

Sin := funcenv(Sin):
Sin::expand := proc(u) // compute expand(Sin(u))
  local x, y;
begin
  // recursively expand the argument u
  u := expand(op(u));

   if type(u) = "_plus" then // u is a sum
    x := op(u, 1); // the first term
    y := u - x;    // the remaining terms

    // apply the addition theorem and
    // expand the result again
    expand(Sin(x)*cos(y) + cos(x)*Sin(y))
  else
    Sin(u)
  end_if
end_proc:

Теперь, если expand сталкивается с подвыражением формы Sin(u), это вызывает Sin::expand(u), чтобы расширить Sin(u). Следующая команда сначала расширяет аргумент a*(b+c) через рекурсивный вызов в Sin::expand, затем применяет теорему сложения, и наконец сам expand расширяет продукт результата с z:

expand(z*Sin(a*(b + c)))

Расширение после приложения теоремы сложения в Sin::expand необходимо, чтобы обработать случай, когда u является суммой больше чем с двумя условиями: затем y является снова суммой, и cos(y) и Sin(y) расширены рекурсивно:

expand(Sin(a + b + c))

Возвращаемые значения

арифметическое выражение.

Перегруженный

f