Документация

Введение

Обзор всех доступных функций может быть получен при помощи функции MuPAD^® info. Здесь мы видим извлечение функций, доступных в библиотеке линейной алгебры (мы не утверждаем целый вывод, сгенерированный вызовом info(linalg), поскольку библиотека содержит больше чем 40 различных функций):

info(linalg)

Library 'linalg': the linear algebra package

 -- Interface:
linalg::addCol,           linalg::addRow,
linalg::adjoint,          linalg::angle,
linalg::basis,            linalg::charmat,
linalg::charpoly,         linalg::col,
...

Будучи экспортированным, библиотечные функции могут также использоваться их коротким обозначением. Вызов функции use (linalg) экспортирует все функции linalg. После того, как тот может использовать имя функции gaussElim вместо linalg::gaussElim, например.

Обратите внимание на то, что пользовательские процедуры, которые используют функции библиотеки linalg, должны всегда использовать длинное обозначение linalg::functionname в порядке убедиться, что однозначность имени функции гарантируется.

Самый легкий способ задать матричный A использует команду matrix. Следующее задает 2×2 матрица:

A := matrix([[1, 2], [3, 2]])

Теперь, можно добавить или умножить матрицы с помощью стандартных арифметических операторов MuPAD:

A * A, 2 * A, 1/A

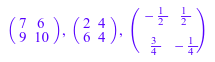
Далее, можно использовать функции библиотеки linalg:

linalg::det(A)

Доменным типом, возвращенным matrix, является Dom::Matrix ():

domtype(A)

который введен в следующем разделе.

Типы данных для матриц и векторов

• Комментарии по улучшению времени выполнения

Библиотека linalg основана на областях Dom::Matrix и Dom::SquareMatrix. Эти конструкторы позволяют пользователю задать матрицы, и они предлагают матричную арифметику и несколько функций для матричной манипуляции.

Область, созданная Dom::Matrix, представляет матрицы произвольных строк и столбцов по заданному звонку. Доменный конструктор Dom::Matrix ожидает содействующий звонок категории Cat::Rng (звонок без модуля) в качестве аргумента. Если никакой аргумент не дан, область матриц создается, который представляет матрицы по полю арифметических выражений, т.е. доменный Dom::ExpressionField ().

Будьте осторожны с вычислениями с матрицами по этой содействующей области, потому что их записи обычно не имеют уникального представления (например, существует больше чем одно представление нуля). Можно нормировать компоненты такого матричного A с командой map(A, normal ).

Библиотека Dom предлагает стандартные содействующие области, такие как поле рациональных чисел (Dom::Rational), звонок целых чисел (Dom::Integer), классы вычетов целых чисел (Dom::IntegerMod (n)) для целочисленного n, или даже звонки полиномов (такие как Dom::DistributedPolynomial (ind,R) или Dom::Polynomial (R), где ind является списком переменных и R, является содействующим звонком).

Область, созданная доменным конструктором Dom::SquareMatrix, представляет звонок квадратных матриц по заданной содействующей области. Dom::SquareMatrix ожидает количество строк квадратных матриц и опционально содействующего звонка категории Cat::Rng.

Существует несколько возможностей задать матрицы области, созданной Dom::Matrix или Dom::SquareMatrix. Матрица может быть создана путем предоставления двумерного массива, списка матричных компонентов или функции, которая генерирует матричные компоненты:

delete a, b, c, d:
A := matrix([[a, b], [c, d]])

Команда matrix на самом деле является сокращением от доменного Dom::Matrix().

Чтобы создать диагональные матрицы, нужно использовать опцию Diagonal (третий аргумент matrix является или функцией или списком):

B := matrix(2, 2, [2, -2], Diagonal)

Следующий двум примерам показывает значение третьего аргумента:

delete x: matrix(2, 2, () -> x), matrix(2, 2, x)

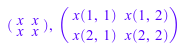
MuPAD арифметические операторы используются, чтобы выполнить матричную арифметику:

A * B - 2 * B

1/A

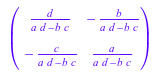
Затем мы создаем 2×2 обобщенная Гильбертова матрица (см. также linalg::hilbert) как матрица звонка двумерных квадратных матриц:

MatQ2 := Dom::SquareMatrix(2, Dom::Rational)

H2 := MatQ2((i, j) -> 1/(i + j - 1))

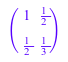
Вектор с компонентами n 1×n матрица (вектор - строка) или n ×1 матрица (вектор-столбец).

К компонентам матрицы или вектора получают доступ с помощью индексного оператора, т.е. A[i,j] возвращает компонент строки с индексом i и столбец с индексом j.

Вход A[i, j]:= x устанавливает (i, j)-th компонент матричного A к значению x.

Индексный оператор может также использоваться, чтобы извлечь подматрицы путем предоставления областей значений целых чисел в качестве его аргументов:

A := Dom::Matrix(Dom::Integer)(
  [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
)

A[1..3, 1..2], A[3..3, 1..3]

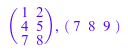
См. также функциональный linalg::submatrix.

adjoint := proc(A)
    local n, R, i, j, a, Ai, Mat,
          // local variables to store often used methods
          det, delRow, delCol, Rnegate;
begin
    if args(0) <> 1 then
        error("wrong number of arguments")
    end_if;

    Mat := A::dom;       // the domain of A
    R := Mat::coeffRing; // the component ring of A
    n := Mat::matdim(A); // the dimension of A; faster than calling
                         // 'linalg::matdim'!
    if testargs() then
        if Mat::hasProp(Cat::Matrix) <> TRUE then
            error("expecting a matrix")
        elif not R::hasProp( Cat::CommutativeRing ) then
            error("expecting matrix over a 'Cat::CommutativeRing'")
        elif n[1] <> n[2] then
            error("expecting a square matrix")
        end_if
    end_if;

    // store often used methods in local variables:
    det := linalg::det;
    delRow := Mat::delRow;  // faster than calling 'linalg::delRow'!
    delCol := Mat::delCol;  // faster than calling 'linalg::delCol'!
    Rnegate := R::_negate;  // faster than using the '-' operator!

    n := Mat::matdim(A)[1]; // faster than calling 'linalg::nrows'!
    a := array(1..n, 1..n);

    for i from 1 to n do
        Ai := delCol(A, i);
        for j from 1 to n do
            a[i, j] := det(delRow(Ai, j));
            if i + j mod 2 = 1 then
                a[i, j] := Rnegate(a[i, j])
            end_if
        end_for
    end_for;

    // create a new matrix: use Mat::create instead of Mat::new
    // because the entries of the array are already elements of R
    return(Mat::create(a))
end_proc:

MatZ6 := Dom::Matrix(Dom::IntegerMod(6)):
adjoint(MatZ6([[1, 5], [2, 4]]))