Несколько семейств вейвлетов, которые, оказалось, были особенно полезны, включены в этот тулбокс. То, что следует, является введением в некоторые семейства вейвлетов.
Чтобы исследовать все семейства вейвлетов самостоятельно, проверьте инструмент Wavelet Display:
Введите waveletAnalyzer в командной строке MATLAB®. Wavelet Analyzer появляется.
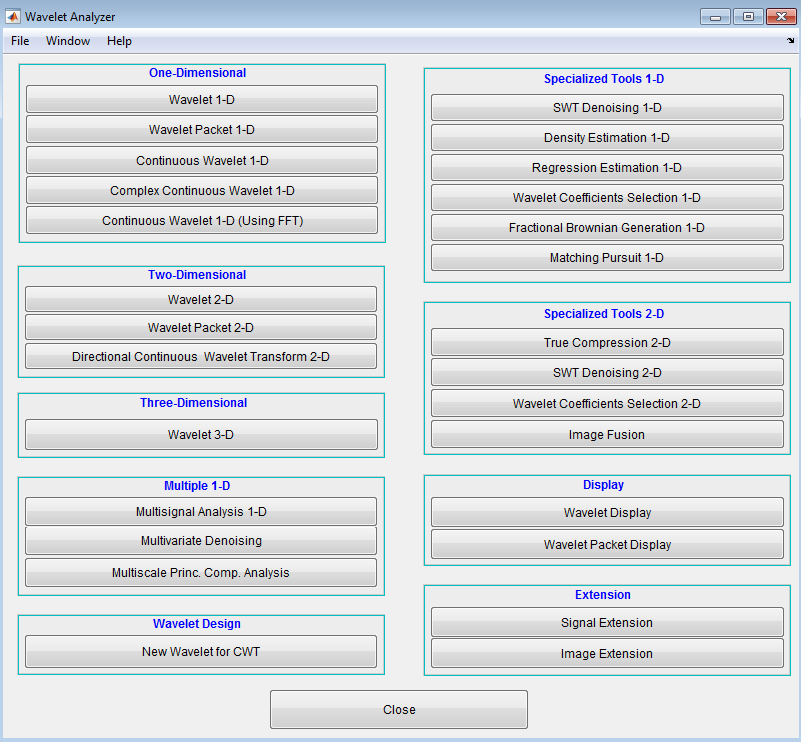
Кликните по элементу Меню отображения Вейвлета. Инструмент Wavelet Display появляется.
Выберите семейство из меню Wavelet в правом верхнем из инструмента.
Кликните по Кнопке отображения. Изображения вейвлетов и их связанных фильтров появляются.
Получите больше информации путем нажатия на кнопки информации, расположенные справа.
Любое обсуждение вейвлетов начинается с вейвлета Хаара, первого и самого простого. Вейвлет Хаара прерывист, и напоминает ступенчатую функцию. Это представляет тот же вейвлет как Daubechies db1.
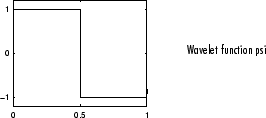
Ингрид Добечис, одна из самых ярких звезд в мире исследования вейвлета, изобрела то, что называется сжато поддерживаемыми ортонормированными вейвлетами — таким образом создание дискретного реального анализа вейвлета.
Именами вейвлетов семейства Daubechies является записанный dbN, где N является порядком и db “фамилия” вейвлета. Вейвлет db1, как упомянуто выше, совпадает с вейвлетом Haar. Вот функции вейвлета psi следующих девяти членов семейства:
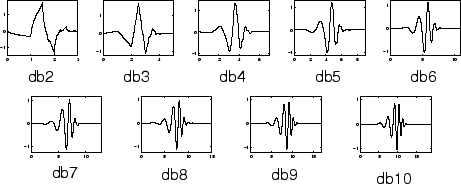
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('db') из командной строки MATLAB. См. Вейвлеты Daubechies: dbN в Руководстве пользователя Wavelet Toolbox для большего количества детали.
Это семейство вейвлетов показывает свойство линейной фазы, которая необходима для реконструкции изображений и сигнала. При помощи двух вейвлетов, один для разложения (на левой стороне) и другой для реконструкции (на правой стороне) вместо того же самого одно, выведены интересные свойства.
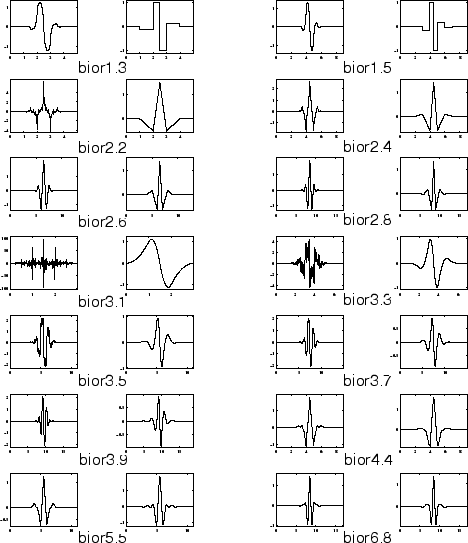
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('bior') из командной строки MATLAB. Смотрите Биоортогональные Пары Вейвлета: biorNr. Без обозначения даты в Руководстве пользователя Wavelet Toolbox для большего количества детали.
Созданный мной. Daubechies по требованию Р. Койфмана. Функция вейвлета имеет 2N, моменты, равные 0 и масштабирующаяся функция, имеют 2N-1 моменты, равные 0. Две функции имеют поддержку длины 6N-1. Можно получить обзор основных свойств этого семейства путем ввода waveinfo('coif') из командной строки MATLAB. См. Вейвлеты Coiflet: coifN в Руководстве пользователя Wavelet Toolbox для большего количества детали.

symlets являются почти симметричными вейвлетами, предложенными Daubechies как модификации семейству db. Свойства двух семейств вейвлетов подобны. Вот функции вейвлета psi.
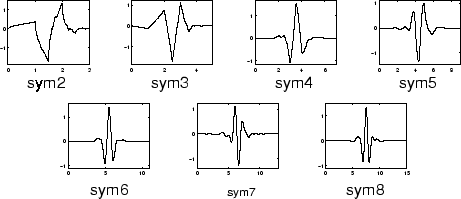
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('sym') из командной строки MATLAB. См. Вейвлеты Symlet: symN в Руководстве пользователя Wavelet Toolbox для большего количества детали.
Этот вейвлет не имеет никакой функции масштабирования, но является явным.
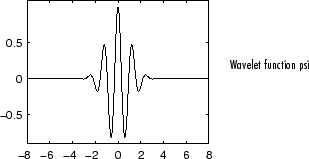
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('morl') из командной строки MATLAB. См. Вейвлет Morlet: morl в Руководстве пользователя Wavelet Toolbox для большего количества детали.
Этот вейвлет не имеет никакой функции масштабирования и выведен от функции, которая пропорциональна второй производной функции Гауссовой функции плотности вероятности. Это, также знает как вейвлет Ricker.
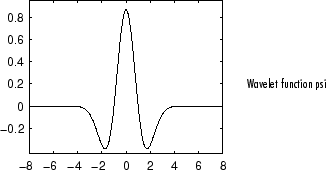
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('mexh') из командной строки MATLAB. Смотрите мексиканский Вейвлет Шляпы: mexh в Руководстве пользователя Wavelet Toolbox для получения дополнительной информации.
Вейвлет Мейера и масштабирующий функцию задан в частотном диапазоне.
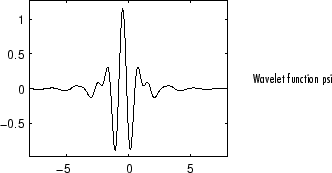
Можно получить обзор основных свойств этого семейства путем ввода waveinfo('meyer') из командной строки MATLAB. Смотрите Вейвлет Мейера: meyr в Руководстве пользователя Wavelet Toolbox для большего количества детали.
Некоторые другие действительные вейвлеты доступны в тулбоксе:
Биоортогональный реверс
Гауссово семейство производных
Основанное на КИХ приближение вейвлета Мейера
Смотрите Дополнительные Действительные Вейвлеты в Руководстве пользователя Wavelet Toolbox для получения дополнительной информации.
Некоторые комплексные семейства вейвлетов доступны в тулбоксе:
Гауссовы производные
Morlet
B-сплайн частоты
Шеннон
Смотрите Комплексные Вейвлеты в Руководстве пользователя Wavelet Toolbox для получения дополнительной информации.