Семейства вейвлетов

Программное обеспечение Wavelet Toolbox™ включает большое количество вейвлетов, которые можно использовать и для непрерывного и для дискретного анализа. Для дискретного анализа примеры включают ортогональные вейвлеты (экстремальная фаза Добечиса и наименьшее количество асимметричных вейвлетов) и B-сплайн биоортогональные вейвлеты. Для непрерывного анализа программное обеспечение Wavelet Toolbox включает Morlet, Мейера, производную Гауссовых, и вейвлеты Пола.

Выбор вейвлета диктуют сигнал или характеристики изображений и природа приложения. Если вы понимаете свойства вейвлета анализа и синтеза, можно выбрать вейвлет, который оптимизирован для приложения.

Семейства вейвлетов отличаются с точки зрения нескольких важных свойств. Примеры включают:

Поддержка вейвлета вовремя и частоты и уровня затухания.
Симметрия или антисимметрия вейвлета. Сопроводительные совершенные фильтры реконструкции имеют линейную фазу.
Номер исчезающих моментов. Вейвлеты с растущими числами исчезающих моментов приводят к разреженным представлениям для большого класса сигналов и изображений.
Регулярность вейвлета. Более сглаженные вейвлеты обеспечивают более резкое разрешение частоты. Кроме того, итеративные алгоритмы для конструкции вейвлета сходятся быстрее.
Существование масштабирующейся функции, φ.

Для непрерывного анализа, программное обеспечение Wavelet Toolbox аналитический основанный на вейвлете анализ для избранных вейвлетов. Смотрите cwt и icwt для деталей. Обратное Непрерывное Преобразование Вейвлета для основной теоретической мотивации. Реконструкция сигнала от Непрерывных Коэффициентов Преобразования Вейвлета иллюстрирует использование обратного непрерывного вейвлета преобразовывает (CWT) для моделируемых и реальных сигналов.

Ввод waveinfo в командной строке отображает обзор основных свойств доступных семейств вейвлетов. Для определенного семейства вейвлетов используйте waveinfo с кратким названием семейства вейвлетов. Можно найти краткие названия семейства вейвлетов перечисленными в следующей таблице и на странице с описанием для waveinfo.

Краткое название семейства вейвлетов	Фамилия вейвлета
`'haar'`	Вейвлет Хаара
`'db'`	Вейвлеты Daubechies
`'sym'`	Symlets
`'coif'`	Coiflets
`'bior'`	Биоортогональные вейвлеты
`'rbio'`	Инвертируйте биоортогональные вейвлеты
`'meyr'`	Вейвлет Мейера
`'dmey'`	Дискретное приближение вейвлета Мейера
`'gaus'`	Гауссовы вейвлеты
`'mexh'`	Мексиканский вейвлет шляпы (также известный как вейвлет Ricker)
`'morl'`	Вейвлет Morlet
`'cgau'`	Объедините Гауссовы вейвлеты
`'shan'`	Шенноновские вейвлеты
`'fbsp'`	Вейвлеты B-сплайна частоты
`'cmor'`	Объедините вейвлеты Morlet
`'fk'`	Вейвлеты Фейера-Коровкина

Отобразить подробную информацию о наименьшем количестве асимметричных ортогональных вейвлетов Добечиса, введите:

waveinfo('sym')

Чтобы вычислить вейвлет и масштабирующий функцию (при наличии), используйте wavefun.

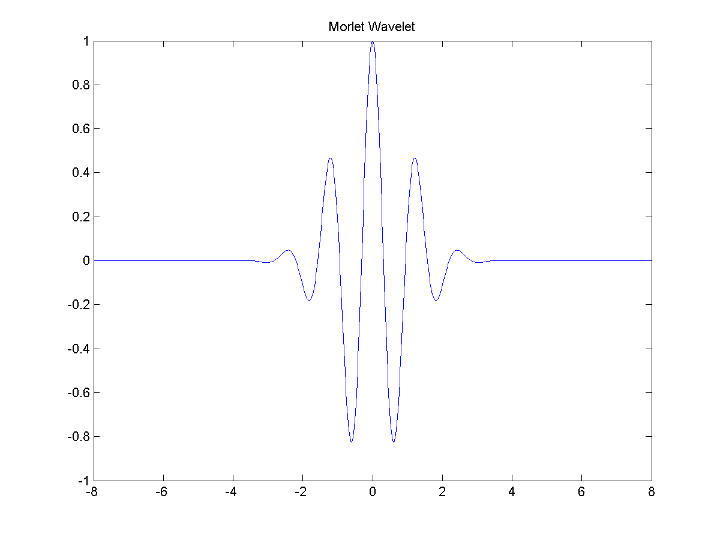
Вейвлет Morlet подходит для непрерывного анализа. Нет никакой функции масштабирования, сопоставленной с вейвлетом Morlet. Чтобы вычислить вейвлет Morlet, можно войти:

[psi,xval] = wavefun('morl',10);
plot(xval,psi); title('Morlet Wavelet');

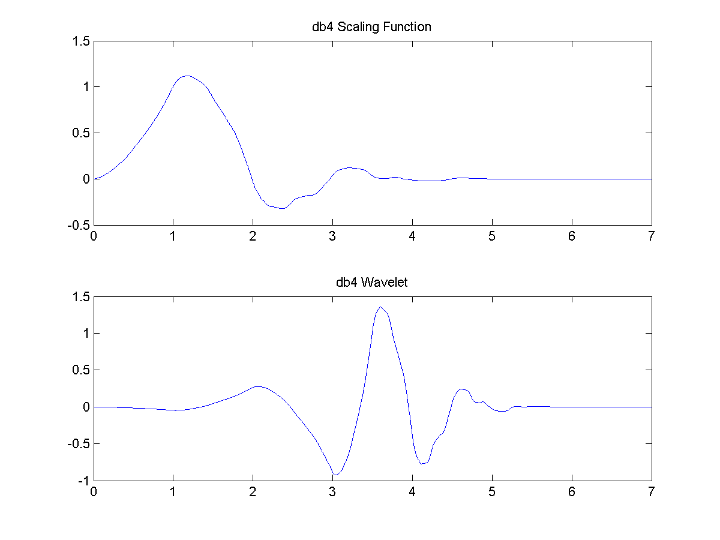
Для вейвлетов, сопоставленных с анализом мультиразрешения, можно вычислить и масштабирующуюся функцию и вейвлет. Следующий код возвращает масштабирующуюся функцию и вейвлет для экстремального вейвлета фазы Добечиса с 4 исчезающими моментами.

[phi,psi,xval] = wavefun('db4',10);
subplot(211);
plot(xval,phi);
title('db4 Scaling Function');
subplot(212);
plot(xval,psi);
title('db4 Wavelet');

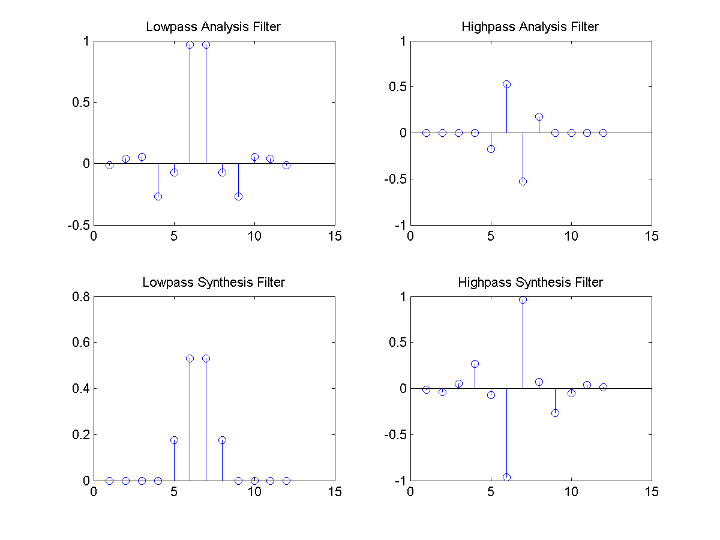
В дискретном анализе вейвлета фильтры анализа и синтеза более интересны, чем связанная функция масштабирования и вейвлет. Можно использовать wfilters, чтобы получить фильтры анализа и синтеза.

Получите разложение (анализ) и реконструкция (синтез) фильтры для B-сплайна биоортогональный вейвлет. Задайте 3 исчезающих момента в вейвлете синтеза и 5 исчезающих моментов в аналитическом вейвлете. Постройте импульсные ответы фильтров.

[LoD,HiD,LoR,HiR] = wfilters('bior3.5');
subplot(221);
stem(LoD);
title('Lowpass Analysis Filter');
subplot(222);
stem(HiD);
title('Highpass Analysis Filter');
subplot(223);
stem(LoR);
title('Lowpass Synthesis Filter');
subplot(224);
stem(HiR);
title('Highpass Synthesis Filter');

Вейвлеты Daubechies: dbN

Вейвлеты dbN являются экстремальными вейвлетами фазы Добечиса. N относится к номеру исчезающих моментов. Эти фильтры также упомянуты в литературе количеством касаний фильтра, которое является 2N. Больше об этом семействе может быть найден на странице 195 [Dau92]. Введите waveinfo('db') в командной строке MATLAB^®, чтобы получить обзор основных свойств этого семейства.

Вейвлеты Daubechies db4 слева и db8 справа

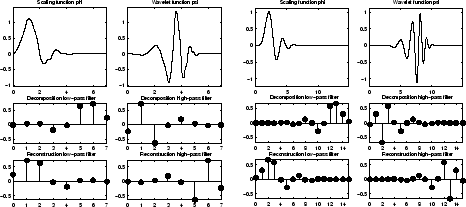
Вейвлет db1 также известен как вейвлет Хаара. Вейвлет Хаара является единственным ортогональным вейвлетом с линейной фазой. Используя waveinfo('haar'), можно получить обзор основных свойств этого вейвлета.

Вейвлеты Symlet: symN

Вейвлеты symN также известны как Добечиса меньше всего - асимметричные вейвлеты. symlets более симметричны, чем экстремальные вейвлеты фазы. В symN N является номером исчезающих моментов. Эти фильтры также упомянуты в литературе количеством касаний фильтра, которое является 2N. Больше о symlets может быть найден в [Dau92], страницах 198, 254-257. Введите waveinfo('sym') в подсказке команды MATLAB, чтобы получить обзор основных свойств этого семейства.

Symlets sym4 слева и sym8 справа

Вейвлеты Coiflet: coifN

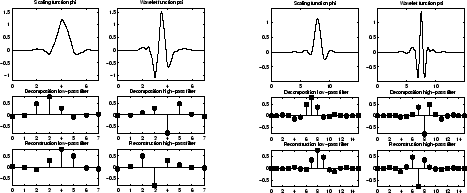
Coiflet, масштабирующие функции также, показывают исчезающие моменты. В coifN N является номером исчезающих моментов и для вейвлета и для масштабирующихся функций. Эти фильтры также упомянуты в литературе количеством коэффициентов фильтра, которое является 3N. Для coiflet конструкции смотрите страницы 258-259 [Dau92]. Введите waveinfo('coif') в подсказке команды MATLAB, чтобы получить обзор основных свойств этого семейства.

Coiflets coif3 слева и coif5 справа

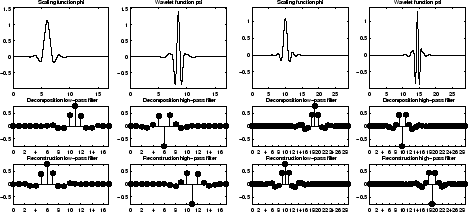
Если s является достаточно регулярным непрерывным сигналом времени для большого j коэффициент $〈 s, ϕ_{- j, k} 〉$ аппроксимирован $2^{- j / 2} s (2^{- j} k)$ .

Если s является полиномом степени d, d ≤ N – 1, приближение становится равенством. Это свойство используется, соединяется с выборкой проблем, при вычислении различия между расширением по φ_{j, l} данного сигнала и его выбранной версией.

Биоортогональные Пары Вейвлета: biorNr. Без обозначения даты

В то время как вейвлет Хаара является единственным ортогональным вейвлетом с линейной фазой, можно разработать биоортогональные вейвлеты с линейной фазой.

Биоортогональные вейвлеты показывают пару масштабирования функций и сопоставленных масштабирующихся фильтров — один для анализа и один для синтеза.

Существует также пара вейвлетов и сопоставленных фильтров вейвлета — один для анализа и один для синтеза.

Вейвлеты анализа и синтеза могут иметь различные числа исчезающих моментов и свойств регулярности. Можно использовать вейвлет с большим номером исчезающих моментов для анализа, приводящего к разреженному представлению, в то время как вы используете более сглаженный вейвлет для реконструкции.

Смотрите страницы 259, 262-85 и [Coh92] [Dau92] для получения дополнительной информации о конструкции биоортогональных основ вейвлета. Введите waveinfo('bior') в командной строке, чтобы получить обзор основных свойств этого семейства.

Следующий код возвращает B-сплайн биоортогональные фильтры реконструкции и разложения с 3 и 5 исчезающими моментами и строит импульсные ответы.

Импульсные ответы фильтров lowpass симметричны относительно средней точки. Импульсные ответы фильтров highpass антисимметричны относительно средней точки.

[LoD,HiD,LoR,HiR] = wfilters('bior3.5');
subplot(221);
stem(LoD);
title('Lowpass Analysis Filter');
subplot(222);
stem(HiD);
title('Highpass Analysis Filter');
subplot(223);
stem(LoR);
title('Lowpass Synthesis Filter');
subplot(224);
stem(HiR);
title('Highpass Synthesis Filter');

Противоположные Биоортогональные Пары Вейвлета: rbioNr. Без обозначения даты

Это семейство получено из биоортогональных пар вейвлета, ранее описанных.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('rbio') из командной строки MATLAB.

Инвертируйте Биоортогональный Вейвлет rbio1.5

Вейвлет Мейера: meyr

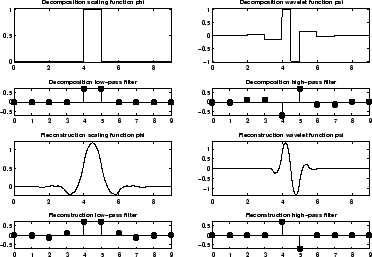
И ψ и φ заданы в частотном диапазоне, начиная со вспомогательной функции ν (см. страницы 117, 119, 137, 152 [Dau92]). Путем ввода waveinfo('meyr') в подсказке команды MATLAB можно получить обзор основных свойств этого вейвлета.

Вейвлет Мейера

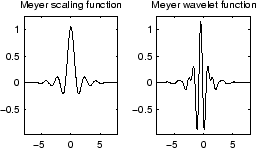
Вейвлет Мейера и масштабирующий функцию задан в частотном диапазоне:

Функция вейвлета

$\begin{array}{l} \hat{ψ} (ω) = (^{2 π) - 1 / 2} e^{i ω / 2} \sin (\frac{π}{2} ν (\frac{3}{2 π} | ω | - 1)) i f \frac{2 π}{3} \leq | ω | \leq \frac{4 π}{3} \\ \hat{ψ} (ω) = (^{2 π) - 1 / 2} e^{i ω / 2} потому что (\frac{π}{2} ν (\frac{3}{4 π} | ω | - 1)) i f \frac{4 π}{3} \leq | ω | \leq \frac{8 π}{3} \end{array}$
и $\hat{ψ} (ω) = 0 i f | ω | \notin [\frac{2 π}{3}, \frac{8 π}{3}]$
где $ν (a) = a^{4} (35 - 84 a + 70 a^{2} - 20 a^{3}) a \in [0, 1]$
Масштабирование функции

$\begin{array}{l} \hat{ϕ} (ω) = (^{2 π) - 1 / 2} i f | ω | \leq \frac{2 π}{3} \\ \hat{ϕ} (ω) = (^{2 π) - 1 / 2} потому что (\frac{π}{2} ν (\frac{3}{2 π} | ω | - 1)) i f \frac{2 π}{3} \leq | ω | \leq \frac{4 π}{3} \\ \hat{ϕ} (ω) = 0 i f | ω | > \frac{4 π}{3} \end{array}$

Путем изменения вспомогательной функции вы получаете семейство различных вейвлетов. Для необходимых свойств вспомогательной функции ν (seeReferences для получения дополнительной информации). Этот вейвлет гарантирует ортогональный анализ.

Функция ψ не имеет конечной поддержки, но ψ уменьшается к 0 когда, быстрее, чем какой-либо обратный полином

$\forall n \in Ν, \exists C_{n}$ таким образом, что $| ψ (x) | \leq C_{n} {(1 + {| x |}^{2})}^{- n}$

Это свойство содержит также для производных

$\forall k \in N, \forall n \in N, \exists C_{k, n}$ , таким образом, что $| ψ^{(k)} x | \leq C_{k, n} (1 + {| x |}^{2}) - n$

Вейвлет бесконечно дифференцируем.

Примечание

Несмотря на то, что вейвлет Мейера сжато не поддержан, там существует хорошее продвижение приближения к КИХ-фильтрам, которые можно использовать в DWT. Введите waveinfo('dmey') в подсказке команды MATLAB, чтобы получить обзор основных свойств этого псевдовейвлета.

Гауссово Семейство Производных: гаусс

Это семейство создается, начиная с Гауссовой функции $f (x) = C_{p} e^{- x^{2}}$ путем взятия производной ^pth f.

Целочисленный p является параметром этого семейства и в предыдущей формуле, _Cp таков что ${‖ f^{(p)} ‖}^{2} = 1$ где f ^(p) является производной ^pth f.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('gaus') из командной строки MATLAB.

Гауссов Производный Вейвлет gaus8

Мексиканский Вейвлет Шляпы: mexh

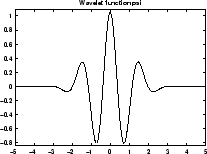
Этот вейвлет пропорционален второй производной функции Гауссовой функции плотности вероятности. Вейвлет является особым случаем более многочисленного семейства вейвлетов производной гауссовых (DOG). Это также известно как вейвлет Ricker.

Нет никакой функции масштабирования, сопоставленной с этим вейвлетом.

Введите waveinfo('mexh') в подсказке команды MATLAB, чтобы получить обзор основных свойств этого вейвлета.

Можно вычислить вейвлет с wavefun.

[psi,xval] = wavefun('mexh',10);
plot(xval,psi);
title('Mexican Hat Wavelet');

Вейвлет Morlet: morl

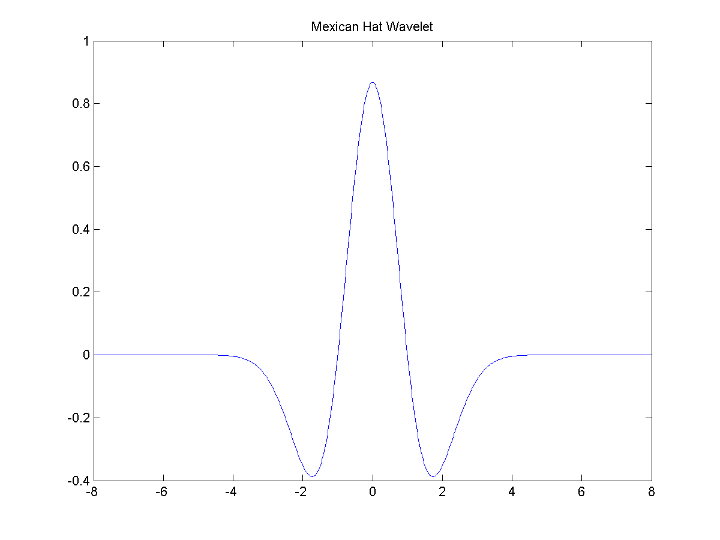
Существуют и версии с комплексным знаком и с действительным знаком этого вейвлета. Введите waveinfo('morl') в командной строке MATLAB, чтобы получить свойства вейвлета Morlet с действительным знаком.

Вейвлет Morlet с действительным знаком задан как:

$ψ (x) = C e^{- x^{2}} потому что (5 x)$

Постоянный C используется для нормализации ввиду реконструкции.

[psi,xval] = wavefun('morl',10);
plot(xval,psi);
title('Real-valued Morlet Wavelet');

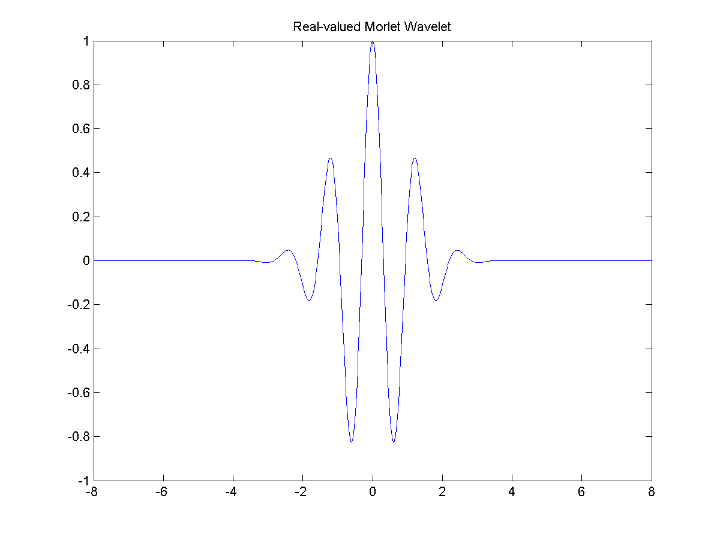
Вейвлет Morlet технически не удовлетворяет условие допустимости..

Дополнительные действительные вейвлеты

Некоторые другие действительные вейвлеты доступны в тулбоксе.

Комплексные вейвлеты

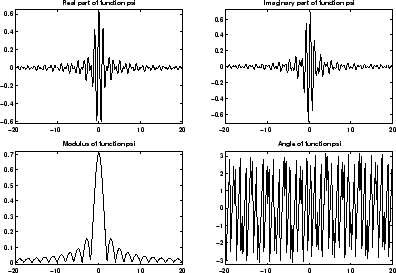
Тулбокс также обеспечивает много вейвлетов с комплексным знаком для непрерывного анализа вейвлета. Вейвлеты с комплексным знаком предоставляют информацию о фазе и поэтому очень важны в анализе частоты времени неустановившихся сигналов.

Комплексные Гауссовы Вейвлеты: cgau

Это семейство создается, начиная с комплексной Гауссовой функции

$f (x) = C_{p} e^{- i x} e^{- x^{2}}$ путем взятия производной ^pth f. Целочисленный p является параметром этого семейства и в предыдущей формуле, _Cp таков что

${‖ f^{(p)} ‖}^{2} = 1$ где f ^(p) является производной ^pth f.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('cgau') из командной строки MATLAB.

Объедините Гауссов Вейвлет cgau8

Комплексные Вейвлеты Morlet: cmor

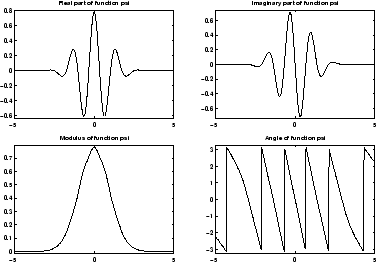
Смотрите страницы 62-65 [Teo98].

Комплексный вейвлет Morlet задан

$ψ (x) = \frac{1}{\sqrt{π f_{b}}} e^{2 i π f_{c} x} e^{\frac{x^{2}}{f^{b}}}$

в зависимости от двух параметров:

_fb является параметром пропускной способности.
_fc является частотой центра вейвлета.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('cmor') из командной строки MATLAB.

Объедините Вейвлет Morlet morl 1.5-1

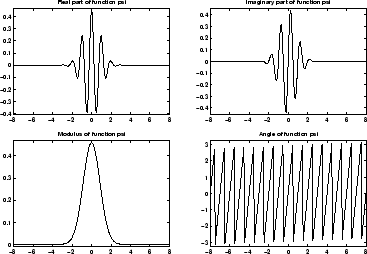
Комплексные Вейвлеты B-сплайна Частоты: fbsp

Смотрите страницы 62-65 [Teo98].

Комплексный вейвлет B-сплайна частоты задан

$ψ (x) = \sqrt{f_{b}} {(sinc (\frac{f_{b} x}{m}))}^{m} e^{2 i π f_{c} x}$

в зависимости от трех параметров:

m является целочисленным параметром порядка (m ≥ 1).
_fb является параметром пропускной способности.
_fc является частотой центра вейвлета.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('fbsp') из командной строки MATLAB.

Комплексный Вейвлет B-сплайна Частоты fbsp 2-0.5-1

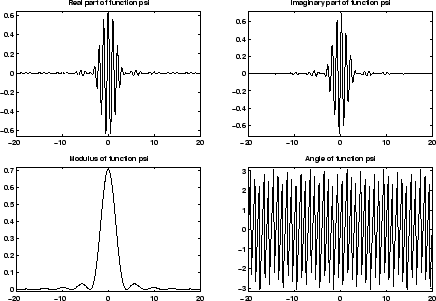
Комплексные Шенноновские Вейвлеты: shan

Смотрите страницы 62-65 [Teo98].

Это семейство получено из вейвлетов B-сплайна частоты установкой m к 1.

Комплекс вейвлет Шеннона задан

$ψ (x) = \sqrt{f_{b}} sinc (f_{b} x) e^{2 i π f_{c} x}$

в зависимости от двух параметров:

_fb является параметром пропускной способности.
_fc является частотой центра вейвлета.

Можно получить обзор основных свойств этого семейства путем ввода waveinfo('shan') из командной строки MATLAB.

Объедините Шенноновский Вейвлет shan 0.5-1

Документация