Неустановившиеся кадры Габора и постоянное-Q преобразование

Неустановившиеся кадры Габора позволяют вам реализовать адаптивный временем или адаптивный частотой анализ сигналов. Функции cqt и icqt используют неустановившиеся кадры Габора, чтобы получить постоянное-Q (адаптивное частотой) преобразование (CQT) сигнала. Известная сила неустановившихся кадров Габора - то, что они включают конструкцию стабильных инверсий, приводя к совершенной реконструкции.

Теория неустановившихся кадров Габора и эффективные алгоритмы для их реализации происходят из-за Dörfler, Holighaus, Гриля и Velasco [1][2]. Алгоритмы в [1] и [2] реализуют заблокированную фазой версию CQT, который не сохраняет те же фазы, которые были бы получены наивной сверткой. В [3], Schörkhuber, Klapuri, Holighaus и Dörfler разрабатывают эффективные алгоритмы для CQT и обратных CQT, которые действительно подражают коэффициентам, полученным наивной сверткой. Большой Аналитический Тулбокс Частоты Времени [4] обеспечивает обширный набор алгоритмов для неустановившегося анализа Габора и синтеза.

В стандарте анализ Габора окно фиксированного размера размещает плоскость частоты времени рядом. Неустановившийся кадр Габора является набором функций работы с окнами различных размеров, которые используются, чтобы разместить плоскость частоты времени рядом. Анализ вейвлета размещает плоскость частоты времени рядом подобным образом. У вас есть гибкость, чтобы изменить плотность выборки вовремя или частоту. Неустановившиеся кадры Габора полезны в областях, таких как обработка звукового сигнала, где окна частоты времени фиксированного размера не оптимальны. В отличие от кратковременного преобразования Фурье, окна, используемые в постоянном-Q преобразовании, имеют адаптируемую пропускную способность и плотность выборки. В пространстве частоты окна сосредоточены на логарифмически расположенных с интервалами центральных частотах.

Разложение плоскости частоты времени

Преобразование Фурье f (t) является корреляцией f (t) с ^{ej ω t}:

$F (ω) = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t .$

С тех пор ^{ej ω t} не имеет компактной поддержки, преобразование Фурье не является идеальным выбором для изучения неустановившихся сигналов. Если содержимое частоты сигнала изменяется в зависимости от времени, преобразование Фурье не получает то, что те изменения или когда те изменения происходят. Раздел плоскости частоты времени, показанной здесь, представляет это поведение преобразования Фурье.

Чтобы выполнить анализ частоты времени неустановившегося сигнала, запустите с ровной функции работы с окнами с действительным знаком, $g (t)$ , который является эффективно ненулевым только на конечном интервале и имеет норму, равную одной. Кроме того, преобразование Фурье $g (t)$ сосредоточен в нуле и lowpass. Затем, окно f (t) с переводит $g (t)$ . Затем возьмите преобразование Фурье результата

$S F (u, ζ) = \int f (t) g (t - u) e^{- j ζ t} d t .$

Корреляция f (t) с атомами Габора, $g (t - u) e^{j ζ t}$ , стандартный анализ Габора. Путем варьирования u, вы рассматриваете только значения f (t) около времени u. Поддержка $g (t)$ определяет размер окружения около времени u. Преобразование Фурье $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ перевод ζ преобразования Фурье $g (t)$ и дают

${\hat{g}}_{u, ζ} (ω) = e^{- (ω - ζ)} \hat{g} (ω - ζ) .$

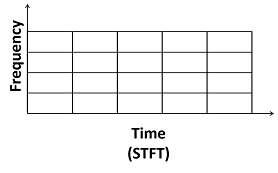
Энергетическая концентрация ${\hat{g}}_{u, ζ} (ω)$ имеет отклонение _σω и сосредоточен в ζ. Если окно, $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ , сдвиги на обычной сетке, преобразовании Фурье продукта переключенного окна и f (t) являются кратковременным преобразованием Фурье (STFT). Мозаичное размещение STFT плоскости частоты времени может быть представлено как сетка полей, каждый сосредоточенный в (u, ζ):

Набор функций ${g_{u, ζ}}$ известен как кадр Габора. Элементы этого набора называются атомами Габора. Кадр является набором функций, {_hk (t)}, которые удовлетворяют следующее условие: там существуйте константы A> 0, B> 0 таким образом это для любой функции f (t),

$A ‖ f ‖^{2} \leq Σ_{k} | < f, h_{k} > |^{2} \leq B ‖ f ‖^{2} .$

Энергетическая концентрация $g (t)$ , вовремя, имеет отклонение _σt. Энергетическая концентрация $\hat{g} (ω)$ , в частоте, имеет отклонение _σω. Энергетическая концентрация определяет, как хорошо окно локализует сигнал вовремя и частоту. Принципом неуверенности частоты времени существует предел относительно того, как хорошо можно одновременно локализовать в обоих временных и частотных диапазонах, как обозначено

$σ_{t} σ_{ω} \geq \frac{}{12} .$

Сужение окна в одной области приводит к более плохой локализации в другой области. Габор показал, что область окна минимальна когда $g (t)$ является Гауссовым.

Постоянное-Q преобразование

В CQT отличаются пропускная способность и плотность выборки в частоте. Окна создаются и применяются непосредственно в частотном диапазоне. Различные окна имеют различные центральные частоты и пропускную способность, но отношение центральной частоты к пропускной способности остается постоянным. Поддержание постоянного отношения подразумевает:

Разрешение вовремя улучшается на более высоких частотах.
Разрешение в частоте улучшается на более низких частотах.

Временные сдвиги для каждого окна зависят от пропускной способности, из-за принципа неуверенности.

CQT зависит от:

_GK функций окна является четными функциями с действительным знаком. В частотном диапазоне преобразование Фурье _GK задано на интервале, [-Fs/2, Фс/2].
Уровень выборки, _ζs.
Количество интервалов на октаву, b.
Минимальные и максимальные частоты, _ζmin и _ζmax.

Выберите минимальную частоту _ζmin и количество интервалов на октаву b. Затем, сформируйте последовательность из геометрически расположенных с интервалами частот,

_ζk = _ζmin × ^2k/b

для k = 0..., K, где K является целым числом, таким образом, что _ζK является самой большой частотой строго меньше, чем частота Найквиста _ζs/2. Пропускная способность на kth частоте установлена в _Ωk = _ζk+1-ζk-1. Учитывая эту выборку, отношение частоты центра kth к пропускной способности окна независимо от k:

Q = _ζk/Δk = ^(21/b-2-1/b)^-1.

Чтобы гарантировать совершенную реконструкцию, компонент DC и частота Найквиста предварительно ожидаются и добавляются, соответственно, к последовательности.

W (ω) формирует _GK функций окна. W (ω) является с действительным знаком, даже непрерывная функция, которая сосредоточена в 0, положительный в интервале [-½,½], и 0 в другом месте. W (ω) переводится в каждую центральную частоту _ζk затем масштабируемый. При оценке масштабированной и переведенной версии W (ω) приводит к содействующему _GK фильтра [m], данный

_GK [m] = W ((m _ζs/L - _ζk)_/Ωk)

для m = 0, …, L-1, где L является длиной сигнала. По умолчанию cqt использует окно 'hann'.

Принципом неуверенности размер пропускной способности ограничивает значение временных сдвигов. Чтобы удовлетворить неравенство кадра, сдвиг _akof _GK должен удовлетворить

_ak ≤ _ζk/Ωk.

Как упомянуто ранее, окно применяется в частотном диапазоне. Фильтры, _GK, сосредоточенный в _ζk, сформированы и применены преобразование Фурье сигнала. Взятие обратного преобразования получает постоянные-Q коэффициенты.

Ссылки

[1] Holighaus, N., М. Дерфлер, Г.А. Веласко и Т. Грилл. "Среда для обратимых постоянных-Q преобразований в реальном времени". Транзакции IEEE на Аудио, Речи и Обработке Языка. Издание 21, № 4, 2013, стр 775–785.

[2] Веласко, G. A. Н. Холайос, М. Дерфлер и Т. Грилл. "Создавая обратимое постоянное-Q преобразование с неустановившимися кадрами Габора". В Продолжениях 14-й Международной конференции по вопросам Эффектов Цифрового аудио (DAFx-11). Париж, Франция: 2011.

[3] Schörkhuber, C., А. Клапури, Н. Холайос и М. Дерфлер. "Тулбокс MATLAB для Эффективных Совершенных Преобразований Частоты Времени Реконструкции с Разрешением Логарифмической Частоты". Представленный AES 53-я Международная конференция по вопросам Семантического Аудио. Лондон, Великобритания: 2014.

[4] Průša, Z., П. Л. Сындергэард, Н. Холайос, К. Висмеир и П. Бэлэзс. Большой Аналитический Тулбокс Частоты Времени 2.0. Звук, Музыка, и Движение, Примечания Лекции в Информатике 2014, стр 419-442. https://github.com/ltfat

Смотрите также

cqt | icqt

Документация