Дискретный стационарный вейвлет преобразовывает 2D
SWC = swt2(X,N,'wname')
[A,H,V,D]
= swt2(X,N,'wname')
SWC = swt2(X,N,Lo_D,Hi_D)
[A,H,V,D]
= swt2(X,N,Lo_D,Hi_D)
swt2 выполняет многоуровневое 2D стационарное разложение вейвлета с помощью или ортогонального или биоортогонального вейвлета. Укажите, что вейвлет с помощью его имени ('wname', видят wfilters для получения дополнительной информации), или его фильтры разложения.
SWC = swt2(X,N,' или wname')[A,H,V,D]
= swt2(X,N,' вычислите стационарное разложение вейвлета 2D или 3-D матричного wname')X с действительным знаком на уровне N, с помощью 'wname'.
Если X является 3-D матрицей, третья размерность X должна равняться 3.
N должен быть строго положительным целым числом (см. wmaxlev для получения дополнительной информации), и 2 Н должны разделить size(X,1) и size(X,2).
Размерность X и уровня N определяет размерности выходных параметров.
Если X является 2D матрицей, и N больше, чем 1, выходные параметры [A,H,V,D] являются трехмерными массивами, которые содержат коэффициенты:
Для 1 ≤ i ≤ N, выходная матрица A(:,:,i) содержит коэффициенты приближения уровня i.
Выходные матрицы H(:,:,i), V(:,:,i) и D(:,:,i) содержат коэффициенты деталей уровня i (горизонталь, вертикальная, и диагональная):
SWC = [H(:,:,1:N) ; V(:,:,1:N) ; D(:,:,1:N) ; A(:,:,N)]
Если X является 2D матрицей, и N равен 1, выходные параметры [A,H,V,D] являются 2D массивами, где A содержит коэффициенты приближения, и H, V, и D содержит горизонталь, вертикальные, и диагональные коэффициенты детали, соответственно.
Если X является 3-D матрицей размерности m-by-n-by-3, и N больше, чем 1, выходные параметры [A,H,V,D] являются 4-D массивами размерности m-by-n-by-3-by-N, которые содержат коэффициенты:
Для 1 ≤ i ≤ N и j = 1, 2, 3, выходная матрица A(:,:,j,i) содержит коэффициенты приближения уровня i.
Выходные матрицы H(:,:,j,i), V(:,:,j,i) и D(:,:,j,i) содержат коэффициенты деталей уровня i (горизонталь, вертикальная, и диагональная):
SWC = [H(:,:,1:3,1:N) ; V(:,:,1:3,1:N) ; D(:,:,1:3,1:N) ; A(:,:,1:3,N)]
Если X является 3-D матрицей размерности m-by-n-by-3, и N равен 1, выходные параметры [A,H,V,D] являются 4-D массивами размерности m-by-n-by-1-by-3, которые содержат коэффициенты:
Для j = 1, 2, 3 выходная матрица A(:,:,1,j) содержит коэффициенты приближения.
Выходные матрицы H(:,:,1,j), V(:,:,1,j) и D(:,:,1,j) содержат горизонталь, вертикальные, и диагональные коэффициенты детали, соответственно.
SWC = [H(:,:,1,1:3) ; V(:,:,1,1:3) ; D(:,:,1,1:3) ; A(:,:,1,1:3)]
swt2 использует арифметику с двойной точностью внутренне и возвращает содействующие матрицы с двойной точностью. swt2 предупреждает, если существует потеря точности при преобразовании, чтобы удвоиться.
Чтобы отличить одноуровневое разложение изображения истинного цвета от многоуровневого разложения индексируемого изображения, приближение и детализировать массивы коэффициентов изображений истинного цвета является 4-D массивами. Смотрите Отличают Одноуровневое Изображение Истинного цвета от Многоуровневых Индексируемых Разложений Изображений. Также смотрите примеры Стационарное Преобразование Вейвлета Изображения и Обратное Стационарное Преобразование Вейвлета Изображения.
Если K - разложение уровня выполняется, размерности A, H, V, и массивами коэффициентов D является m-by-n-by-3-by-K.
Если одноуровневое разложение выполняется, размерности A, H, V, и массивами коэффициентов D является m-by-n-by-1-by-3. Начиная с одиночного элемента MATLAB®removes последние размерности по умолчанию, третья размерность массивов коэффициентов является одиночным элементом.
SWC = swt2(X,N,Lo_D,Hi_D) или [A,H,V,D]
= swt2(X,N,Lo_D,Hi_D), вычисляет стационарное разложение вейвлета как в предыдущем синтаксисе, учитывая эти фильтры, как введено:
Lo_D является фильтром нижних частот разложения.
Hi_D является фильтром высоких частот разложения.
Lo_D и Hi_D должны быть той же длиной.
swt2 задан с помощью периодического расширения. Размер приближения и коэффициентов деталей, вычисленных на каждом уровне, равняется размеру входных данных.
Когда X представляет индексируемое изображение, X m-by-n матрица. Если уровнем разложения, N больше, чем 1, выходные массивы SWC или приблизительно, cH, условная цена и CD, является m-by-n-by-N массивы. Если уровнем разложения, N равен 1, выходные массивы SWC или приблизительно, cH, условная цена и CD, является m-by-n массивы.
Когда X представляет изображение истинного цвета, это становится m-by-n-by-3 массив. Этим массивом является m-by-n-by-3 массив, где каждый m-by-n матрица представляет красную, зеленую, или синюю цветную плоскость, конкатенированную по третьему измерению. Если уровнем разложения, N больше, чем 1, выходные массивы SWC или приблизительно, cH, условная цена и CD, является m-by-n-by-3-by-N. Если уровнем разложения, N равен 1, выходные массивы SWC или приблизительно, cH, условная цена и CD, является m-by-n-by-1-by-3.
Для получения дополнительной информации о форматах изображения смотрите страницы с описанием imfinfo и image.
Для изображений алгоритм, подобный одномерному случаю, возможен для двумерных вейвлетов и масштабирующихся функций, полученных из одномерных единиц продуктом тензора.
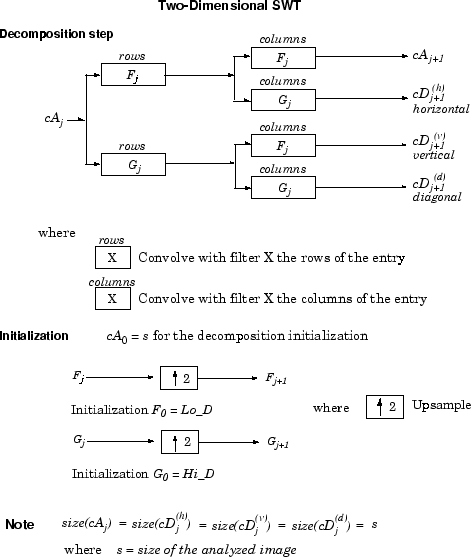
Этот вид двумерного SWT приводит к разложению коэффициентов приближения на уровне j в четырех компонентах: приближение на уровне j +1 и детали в трех ориентациях (горизонталь, вертикальная, и диагональная).
Следующий график описывает основной шаг разложения для изображений:
Нэзон, Г.П.; Б.В. Сильверман (1995), “Стационарный вейвлет преобразовывает и некоторые статистические приложения”, Примечания Лекции в Статистике, 103, стр 281–299.
Койфман, Р.Р.; Донохо, D.L. (1995), “Шумоподавление инварианта перевода”, Примечания Лекции в Статистике, 103, стр 125–150.
Pesquet, Дж.К.; Х. Крим, Х. Карфэйтан (1996), “Независимые от времени ортонормированные представления вейвлета”, Знак Сделки IEEE. Proc., издание 44, 8, стр 1964–1970.