Неподкошенный дискретный стационарный вейвлет преобразовывает (SWTs)

Мы знаем, что классический DWT переносит недостаток: DWT не является независимым от времени преобразованием. Это означает, что, даже с периодическим расширением сигнала, DWT переведенной версии сигнала X не является, в целом, переведенной версией DWT X.

Как восстановить инвариантность перевода, которая желательное имущество утрачено классическим DWT? Идея состоит в том, чтобы составить в среднем некоторый немного отличающийся DWT, названный ε-decimated DWT, чтобы задать стационарный вейвлет преобразовывает (SWT). Это свойство полезно для нескольких приложений, таких как аварийное обнаружение точек.

Главное приложение SWT является шумоподавлением. Для получения дополнительной информации об объяснении см. [CoiD95] в Ссылках. Для примеров смотрите 1D Стационарное Преобразование Вейвлета и 2D Стационарное Преобразование Вейвлета.

Принцип должен составить в среднем несколько сигналов denoised. Каждый из них получен с помощью обычной схемы шумоподавления (см. Шумоподавление Вейвлета и Непараметрическую Функциональную Оценку), но применился к коэффициентам ε-decimated DWT.

Примечание

SWT задан только для сигналов длины, делимой 2^J, где J является максимальным уровнем разложения. SWT использует периодический (per) расширение.

$ε$ - Подкошенный DWT

Что такое ε-decimated DWT?

Там существуйте, много немного отличающихся способов обработать дискретный вейвлет преобразовывает. Давайте вспомним, что основной вычислительный шаг DWT является сверткой, сопровождаемой десятикратным уменьшением. Десятикратное уменьшение сохраняет даже индексированные элементы.

Но десятикратное уменьшение могло быть выполнено путем выбора нечетных индексируемых элементов вместо даже индексируемых элементов. Этот выбор касается каждого шага процесса разложения, таким образом, на каждом уровне мы выбрали нечетный или ровный.

Если мы выполняем все различные возможные разложения исходного сигнала, мы имеем 2^J различные разложения для данного максимального уровня J.

Давайте обозначим ε_j = 1 или 0 выбор нечетных или даже индексируемых элементов на шаге j. Каждое разложение маркировано последовательностью 0s и 1 с: ε = _ε1..., ε_J. Это преобразование называется ε-decimated DWT.

Вы можете получить базисные векторы ε-decimated DWT от тех из стандартного DWT путем применения сдвига и соответствуете специальному выбору источника основных функций.

Как вычислить $ε$ - Подкошенный DWT: SWT

Возможно вычислить весь ε-decimated DWT для данного сигнала длины N путем вычисления приближения и коэффициентов детали для каждой возможной последовательности ε. Сделайте это использование итеративно, немного измененную версию основного шага DWT формы:

[A,D] = dwt(X,wname,'mode','per','shift',e);

Последние два аргумента задают способ выполнить шаг десятикратного уменьшения. Это - классическое для e = 0, но для e = 1 нечетные индексируемые элементы сохраняются десятикратным уменьшением.

Конечно, это не хороший способ вычислить весь ε-decimated DWT, потому что много вычислений много раз выполняются. Мы теперь опишем иначе, который является стационарным вейвлетом преобразовывает (SWT).

Алгоритм SWT очень прост и близко к DWT один. Более точно, для уровня 1, весь ε-decimated DWT (только два на этом уровне) для данного сигнала может быть получен путем свертки к сигналу с соответствующими фильтрами как в случае DWT, но без субдискретизации. Затем приближение и коэффициенты детали на уровне 1 оба имеют размер N, который является длиной сигнала. Это может визуализироваться в следующей фигуре.

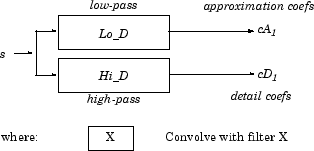
Общий шаг j применяет операцию свертки к коэффициентам приближения на уровне j –1, со сверхдискретизированными версиями соответствующих исходных фильтров, чтобы произвести приближение и коэффициенты детали на уровне j. Это может визуализироваться в следующей фигуре.

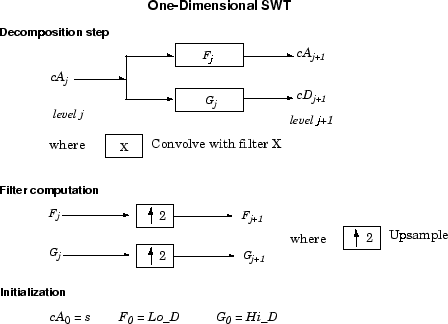
Затем, мы иллюстрируем, как извлечь данный ε-decimated DWT от приближения и содействующей структуры детали SWT.

Мы анализируем последовательность чисел высоты с SWT, на уровне J = 3, с помощью ортогонального вейвлета.

Функциональный swt вычисляет последовательно следующие массивы, где _{A(j,ε1,...,εj)} или _{D(j,ε1,...,εj)} обозначают приближение или коэффициент детали на уровне j, полученный для ε-decimated DWT охарактеризованный ε = _[ε1..., εj].

Шаг 0 (исходные данные)

(0)

Шаг 1

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
(1,0)	(1,1)	(1,0)	(1,1)	(1,0)	(1,1)	(1,0)	(1,1)

Шаг 2

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
D (2,0,0)	D (2,1,0)	D (2,0,1)	D (2,1,1)	D (2,0,0)	D (2,1,0)	D (2,0,1)	D (2,1,1)
(2,0,0)	(2,1,0)	(2,0,1)	(2,1,1)	(2,0,0)	(2,1,0)	(2,0,1)	(2,1,1)

Шаг 3

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
D (2,0,0)	D (2,1,0)	D (2,0,1)	D (2,1,1)	D (2,0,0)	D (2,1,0)	D (2,0,1)	D (2,1,1)
D (3,0,0,0)	D (3,1,0,0)	D (3,0,1,0)	D (3,1,1,0)	D (3,0,0,1)	D (3,1,0,1)	D (3,0,1,1)	D (3,1,1,1)
(3,0,0,0)	(3,1,0,0)	(3,0,1,0)	(3,1,1,0)	(3,0,0,1)	(3,1,0,1)	(3,0,1,1)	(3,1,1,1)

Позвольте j обозначить текущий уровень, где j является также текущим шагом алгоритма. Затем у нас есть следующие абстрактные отношения с _εi = 0 или 1:

[tmpAPP,tmpDET] = 
dwt(A(j,ε₁, ,ɛ_j),wname,'mode','per','shift',ɛ_j+1); 
A(j+1,ɛ₁, ,ɛ_j,ɛ_j+1) = circshift(tmpAPP,-ɛ_j+1);
D(j+1,ɛ₁, ,ɛ_j,ɛ_j+1) = circshift(tmpDET,-ɛ_j+1);

где circshift выполняет ε-circular сдвиг входного вектора. Поэтому, если _εj+1 = 0, инструкция circshift неэффективна и может быть подавлена.

Позвольте ε = [_ε1..., ε_J] с _εi = 0 или 1. Мы имеем 2^J = ²³ = восемь различных ε-decimated DWTs на уровне 3. Выбирая ε, мы можем получить соответствующий ε-decimated DWT из массива SWT.

Теперь, рассмотрите последний шаг, J = 3, и позвольте [Cε, Lε] обозначают структуру разложения вейвлета ε-decimated DWT для данного ε. Затем это может быть получено из структуры разложения SWT путем выбора соответствующих коэффициентов можно следующим образом:

Cε =

(3, _ε1, _ε2, _ε3)

D (3, _ε1, _ε2, _ε3)

D (2, _ε1, _ε2)

D (1, _ε1)

Lε = [1,1,2,4,8]

Например, ε-decimated DWT соответствующий ε = [_ε1, _ε2, _ε3] = [1,0,1] показывают полужирным в последовательности массивов предыдущего примера.

Это может быть расширено к 2D случаю. Алгоритм для стационарного вейвлета преобразовывает для изображений, визуализируется в следующей фигуре.

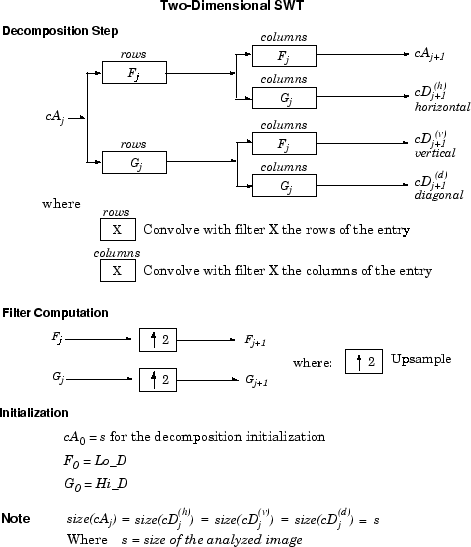
Обратный дискретный стационарный вейвлет преобразовывает (ISWT)

Каждый ε-decimated DWT соответствие данному ε может быть инвертирован.

Чтобы восстановить исходный сигнал с помощью данного ε-decimated DWT охарактеризованный [_ε1..., _εJ], мы можем использовать абстрактный алгоритм

FOR j = J:-1:1
  A(j-1, ε₁, ,ɛ_j-1) = ...
  idwt(A(j,ɛ₁, ,ɛ_j),D(S,ɛ₁, ,ɛ_j)],wname,'mode','per','shift',ɛ_j);
END

Для каждого выбора ε = (_ε1..., _εJ), мы получаем исходный сигнал A (0), начинающий с немного отличающихся разложений и получающий по-разному основные функции анализируемого сигнала.

Идея обратного дискретного стационарного вейвлета преобразовывает, должен составить в среднем инверсии, полученные для каждого ε-decimated DWT. Это может быть сделано рекурсивно, начинающий с уравнивают J к уровню 1.

ISWT получен со следующим абстрактным алгоритмом:

FOR j = J:-1:1
    X0 = idwt(A(j,ɛ₁, ,ɛ_j),D(j,ɛ₁, ,ɛ_j)],wname, ...
            'mode','per','shift',0);
    X1 = idwt(A(j,ɛ₁, ,ɛ_j),D(j,ɛ₁, ,ɛ_j)],wname, ...
            'mode','per','shift',1);
    X1 = circshift(X1,-1);
    A(j-1, ɛ₁, ,ɛ_j-1) = (X0+X1)/2;
END

В том же направлении это может быть расширено к 2D случаю.

Больше о SWT

Некоторые полезные ссылки для Стационарного преобразования вейвлета (SWT) [CoiD95], [NasS95] и [PesKC96] в Ссылках.

Документация