Эта тема берет вас через функции 1D дискретного стационарного анализа вейвлета с помощью программного обеспечения Wavelet Toolbox™. Для получения дополнительной информации смотрите Неподкошенные Дискретные Стационарные Преобразования Вейвлета (SWTs) в Руководстве пользователя Wavelet Toolbox.
Тулбокс обеспечивает эти функции для 1D дискретного стационарного анализа вейвлета. Для получения дополнительной информации о функциях смотрите страницы с описанием.
FunctionName | Цель |
|---|---|
Разложение |
FunctionName | Цель |
|---|---|
Реконструкция |
Стационарная структура разложения вейвлета более послушна, чем вейвлет один. Таким образом, утилиты, полезные для случая вейвлета, не необходимы для стационарного вейвлета преобразовывает (SWT).
В этом разделе вы будете учиться
Загрузите сигнал
Выполните стационарное разложение вейвлета сигнала
Создайте приближения и детали от коэффициентов
Отобразите приближение и деталь на уровне 1
Регенерируйте сигнал при помощи обратного стационарного вейвлета, преобразовывают
Выполните многоуровневое стационарное разложение вейвлета сигнала
Восстановите приближение уровня 3
Восстановите уровень 1, 2 и 3 детали
Восстановите приближения уровня 1 и 2
Отобразите результаты разложения
Восстановите исходный сигнал от разложения уровня 3
Удалите шум из сигнала
Поскольку можно выполнить исследования или из командной строки или из использования приложения Wavelet Analyzer, этот раздел имеет подразделы, покрывающие каждый метод.
Итоговый подраздел обсуждает, как обмениваться сигналом и информацией о коэффициенте между диском и графическими инструментами.
Этот пример включает шумный Доплеровский тестовый сигнал.
Загрузите сигнал.
От подсказки MATLAB® ввести
load noisdopp
Установите переменные. Ввод
s = noisdopp;
Для SWT, если разложение на уровне k необходим, 2^k должен разделиться равномерно на длину сигнала. Если ваш исходный сигнал не имеет правильной длины, можно использовать инструмент Signal Extension в приложении Wavelet Analysis или функции wextend, чтобы расширить его.
Выполните одноуровневое Стационарное Разложение Вейвлета.
Выполните одноуровневое разложение сигнала с помощью вейвлета db1. Ввод
[swa,swd] = swt(s,1,'db1');
Это генерирует коэффициенты приближения уровня 1 (swa) и детали (swd). Оба имеют ту же длину как сигнал. Ввод
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
noisdopp | 1x1024 | 8192 | double array |
s | 1x1024 | 8192 | double array |
swa | 1x1024 | 8192 | double array |
swd | 1x1024 | 8192 | double array |
Отобразите коэффициенты приближения и детали.
Чтобы отобразить коэффициенты приближения и детали на уровне 1, ввести
subplot(1,2,1), plot(swa); title('Approximation cfs')
subplot(1,2,2), plot(swd); title('Detail cfs')
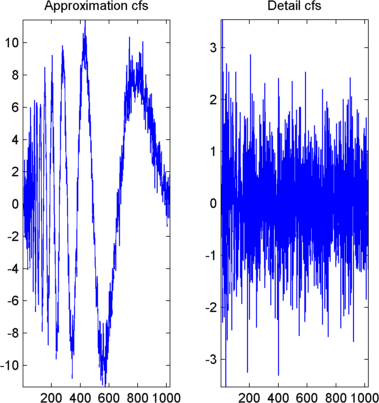
Регенерируйте сигнал Обратным Стационарным Преобразованием Вейвлета.
Чтобы найти обратное преобразование, ввести
A0 = iswt(swa,swd,'db1');
Чтобы проверять совершенную реконструкцию, ввести
err = norm(s-A0) err = 2.1450e-14
Создайте и отобразите приближение и деталь от коэффициентов.
Чтобы создать приближение уровня 1 и деталь (A1 и D1) от коэффициентов swa и swd, ввести
nulcfs = zeros(size(swa)); A1 = iswt(swa,nulcfs,'db1'); D1 = iswt(nulcfs,swd,'db1');
Чтобы отобразить приближение и деталь на уровне 1, ввести
subplot(1,2,1), plot(A1); title('Approximation A1');
subplot(1,2,2), plot(D1); title('Detail D1');
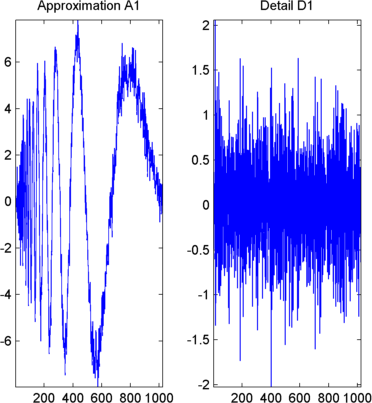
Выполните многоуровневое Стационарное Разложение Вейвлета.
Чтобы выполнить разложение на уровне 3 сигнала (снова использование вейвлета db1), ввести
[swa,swd] = swt(s,3,'db1');
Это генерирует коэффициенты приближений на уровнях 1, 2, и 3 (swa) и коэффициенты деталей (swd). Заметьте, что строки swa и swd являются той же длиной как длина сигнала. Ввод
clear A0 A1 D1 err nulcfs whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
noisdopp | 1x1024 | 8192 | double array |
s | 1x1024 | 8192 | double array |
swa | 3x1024 | 24576 | double array |
swd | 3x1024 | 24576 | double array |
Отобразите коэффициенты приближений и деталей.
Чтобы отобразить коэффициенты приближений и деталей, ввести
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(swa(i,:));
title(['Approx. cfs level ',num2str(i)])
subplot(3,2,kp+2), plot(swd(i,:));
title(['Detail cfs level ',num2str(i)])
kp = kp + 2;
end
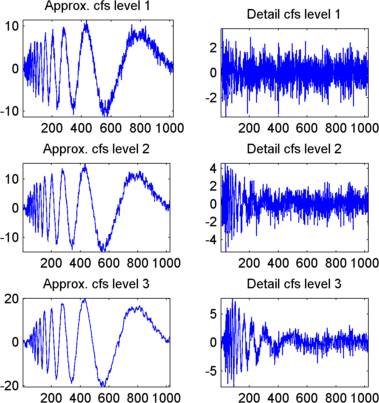
Восстановите приближение на Уровне 3 От коэффициентов.
Чтобы восстановить приближение на уровне 3, ввести
mzero = zeros(size(swd)); A = mzero; A(3,:) = iswt(swa,mzero,'db1');
Восстановите детали от коэффициентов.
Чтобы восстановить детали на уровнях 1, 2 и 3, ввести
D = mzero;
for i = 1:3
swcfs = mzero;
swcfs(i,:) = swd(i,:);
D(i,:) = iswt(mzero,swcfs,'db1');
end
Восстановите и отобразите приближения на Уровнях 1 и 2 от приближения на Уровне 3 и деталей на Уровнях 2 и 3.
Чтобы восстановить приближения на уровнях 2 и 3, ввести
A(2,:) = A(3,:) + D(3,:); A(1,:) = A(2,:) + D(2,:);
Чтобы отобразить приближения и детали на уровнях 1, 2 и 3, ввести
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(A(i,:));
title(['Approx. level ',num2str(i)])
subplot(3,2,kp+2), plot(D(i,:));
title(['Detail level ',num2str(i)])
kp = kp + 2;
end
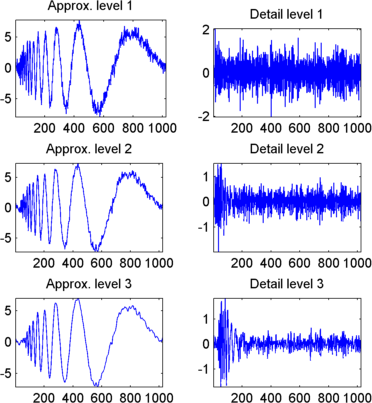
Удалите шум пороговой обработкой.
К denoise сигнал используйте команду ddencmp, чтобы вычислить глобальный порог по умолчанию. Используйте команду wthresh, чтобы выполнить фактическую пороговую обработку коэффициентов детали, и затем использовать команду iswt, чтобы получить сигнал denoised.
Все методы для выбора порогов в 1D Дискретном случае Преобразования Вейвлета также допустимы для 1D Стационарного Преобразования Вейвлета, которые являются также используемыми приложением Wavelet Analysis. Это также верно для 2D преобразований.
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
Чтобы отобразить и оригинал и сигналы denoised, ввести
subplot(2,1,1), plot(s);
title('Original signal')
subplot(2,1,2), plot(clean);
title('denoised signal')
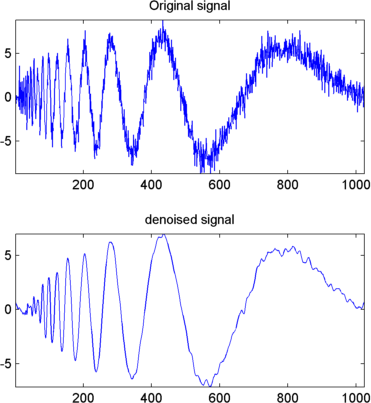
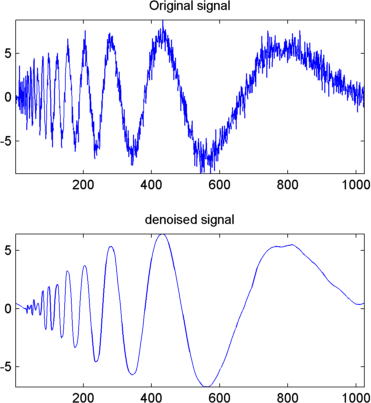
Полученный сигнал остается немного шумным. Результат может быть улучшен путем рассмотрения разложения s на уровне 5 вместо уровня 3 и повторения шагов 14 и 15. Чтобы улучшить предыдущее шумоподавление, ввести
[swa,swd] = swt(s,5,'db1');
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
subplot(2,1,1), plot(s); title('Original signal')
subplot(2,1,2), plot(clean); title('denoised signal')
Второй синтаксис может использоваться для swt и функций iswt, давая те же результаты:
lev = 5; swc = swt(s,lev,'db1'); swcden = swc; swcden(1:end-1,:) = wthresh(swcden(1:end-1,:),sorh,thr); clean = iswt(swcden,'db1');
Можно получить тот же график при помощи тех же команд plot как на шаге 16 выше.
Теперь мы исследуем стратегию к сигналам denoise, на основе 1D стационарного анализа вейвлета с помощью приложения Wavelet Analyzer. Основная идея состоит в том, чтобы составить в среднем много немного отличающихся дискретных исследований вейвлета.
Запустите стационарный вейвлет преобразовывают шумоподавление 1D инструмент.
От посдказки MATLAB введите waveletAnalyzer.
Wavelet Analyzer появляется.
Кликните по пункту меню SWT Denoising 1-D. Дискретный стационарный вейвлет преобразовывает инструмент шумоподавления для 1D сигналов, появляется.
Загрузка данных.
В подсказке команды MATLAB ввести
load noisbloc;
noisbloc. Нажмите ОК, чтобы импортировать шумный сигнал блоков.Выполните стационарное разложение вейвлета.
Выберите вейвлет db1 из меню Wavelet и выберите 5 из меню Level, и затем нажмите Decompose Signal button. После паузы для вычисления инструмент отображает стационарное приближение вейвлета и коэффициенты детали разложения. Они также называются неподкошенными коэффициентами, поскольку они получены с помощью той же схемы что касается DWT, но не использовав шаг десятикратного уменьшения (см. Алгоритм Быстрого преобразования вейвлета (FWT) в Руководстве пользователя Wavelet Toolbox).
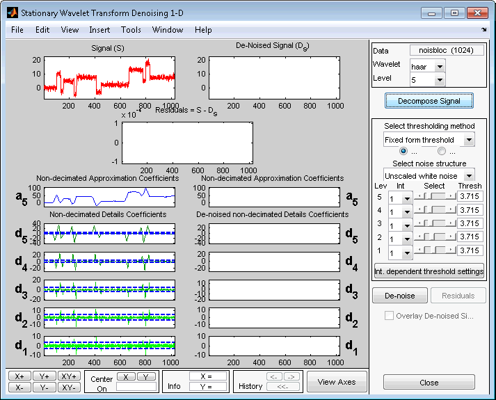
denoise сигнал с помощью Стационарного Преобразования Вейвлета.
В то время как много опций доступны для подстройки алгоритма шумоподавления, мы примем значения по умолчанию фиксированной формы мягкая пороговая обработка и немасштабированный белый шум. Ползунки, расположенные на правильной части окна, управляют зависимыми уровнем порогами, обозначенными желтыми пунктирными линиями, запускающимися горизонтально через графики коэффициентов детали слева от окна. Желтые пунктирные линии могут также быть перетащены непосредственно с помощью левой кнопки мыши по графикам.
Обратите внимание на то, что коэффициенты приближения не являются порогом.
Нажмите denoise кнопку.
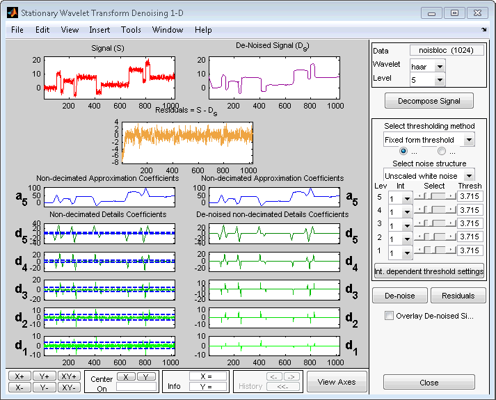
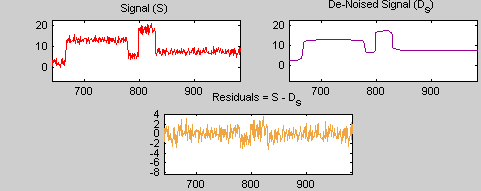
Результат является довольно удовлетворительным, но, кажется, сверхсглаживается вокруг разрывов сигнала. Это видно путем рассмотрения невязок и изменения масштаба на аварийной точке, например, вокруг положения 800.
Выберите трудный для режима пороговой обработки вместо мягкого, и затем нажмите denoise кнопку.
Результат имеет хорошее качество, и невязки похожи на белую шумовую выборку. Чтобы исследовать эту последнюю точку, можно получить больше информации о невязках путем нажатия кнопки Residuals.
Инструмент позволяет вам сохранить сигнал denoised на диск. Тулбокс создает MAT-файл в текущей папке с именем по вашему выбору.
Чтобы сохранить вышеупомянутое denoised сигнал, используйте пункт меню File> Save denoised Сигнал. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения сигнала. Введите имя dnoibloc. После сохранения данных сигнала к файлу dnoibloc.mat загрузите переменные в свою рабочую область:
load dnoibloc whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
dnoibloc | 1x1024 | 8192 | double array |
thrParams | 1x5 | 580 | cell array |
wname | 1x3 | 6 | char array |
Сигнал denoised дан dnoibloc. Кроме того, параметры процесса шумоподавления доступны. Имя вейвлета содержится в wname:
wname
wname =
db1
и зависимые пороги уровня закодированы в thrParams, который является массивом ячеек длины 5 (уровень разложения). Поскольку i от 1 до 5, thrParams{i} содержит нижние и верхние границы интервала пороговой обработки и порогового значения (поскольку зависимые пороги интервала позволены). Для получения дополнительной информации смотрите 1D Адаптивную Пороговую обработку Коэффициентов Вейвлета.
Например, для уровня 1,
thrParams{1}
ans =
1.0e+03 *
0.0010 1.0240 0.0041
Здесь нижняя граница равняется 1, верхняя граница 1024, и пороговое значение 4.1. Общий временной интервал не сегментируется, и процедура не использует зависимые пороги интервала.