Этот раздел берет вас через функции 2D дискретного стационарного анализа вейвлета с помощью программного обеспечения Wavelet Toolbox™.
| FunctionName | Цель |
|---|---|
Разложение |
| FunctionName | Цель |
|---|---|
Реконструкция |
Стационарная структура разложения вейвлета более послушна, чем вейвлет один. Так, утилиты, полезные для случая вейвлета, не необходимы для Стационарного преобразования вейвлета (SWT).
В этом разделе вы будете учиться
Загрузите изображение
Анализируйте изображение
Выполните одноуровневые и многоуровневые разложения изображений и реконструкции (только командная строка)
denoise изображение
В этом примере мы покажем, как можно использовать 2D стационарный анализ вейвлета для denoise изображение.
Вместо того, чтобы использовать image(I), чтобы визуализировать изображение I, мы use image(wcodemat(I)), который отображает перемасштабированную версию продвижения I к более ясному представлению деталей и приближениям (см. страницу с описанием wcodemat).
Этот пример включает изображение, содержащее шум.
Загрузите изображение.
От подсказки MATLAB® ввести
load noiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
Для SWT, если разложение на уровне k необходим, 2^k должен разделиться равномерно на size(X,1) и size(X,2). Если ваше оригинальное изображение не имеет правильного размера, можно использовать Расширение Изображений инструмент приложения Wavelet Analyzer или функциональный wextend, чтобы расширить его.
Выполните одноуровневое Стационарное Разложение Вейвлета.
Выполните одноуровневое разложение изображения с помощью вейвлета db1. Ввод
[swa,swh,swv,swd] = swt2(X,1,'db1');
Это генерирует содействующие матрицы уровня одно приближение (swa) и горизонталь, вертикальные и диагональные детали (swh, swv и swd, соответственно). Оба имеют размер размера изображения. Ввод
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96 | 73728 | double array |
swh | 96x96 | 73728 | double array |
swv | 96x96 | 73728 | double array |
swd | 96x96 | 73728 | double array |
Отобразите коэффициенты приближения и деталей.
Чтобы отобразить коэффициенты приближения и деталей на уровне 1, ввести
map = pink(size(map,1)); colormap(map)
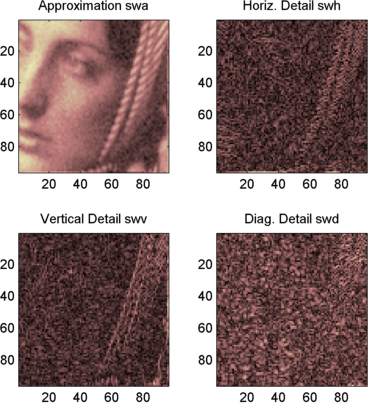
subplot(2,2,1), image(wcodemat(swa,192));
title('Approximation swa')
subplot(2,2,2), image(wcodemat(swh,192));
title('Horiz. Detail swh')
subplot(2,2,3), image(wcodemat(swv,192));
title('Vertical Detail swv')
subplot(2,2,4), image(wcodemat(swd,192));
title('Diag. Detail swd');
Регенерируйте изображение Обратным Стационарным Преобразованием Вейвлета.
Чтобы найти обратное преобразование, ввести
A0 = iswt2(swa,swh,swv,swd,'db1');
Чтобы проверять совершенную реконструкцию, ввести
err = max(max(abs(X-A0)))
err =
1.1369e-13
Создайте и отобразите приближение и детали от коэффициентов.
Чтобы создать приближение уровня 1 и детали (A1, H1, V1 и D1) от коэффициентов swa, swh, swv и swd, вводит
nulcfs = zeros(size(swa)); A1 = iswt2(swa,nulcfs,nulcfs,nulcfs,'db1'); H1 = iswt2(nulcfs,swh,nulcfs,nulcfs,'db1'); V1 = iswt2(nulcfs,nulcfs,swv,nulcfs,'db1'); D1 = iswt2(nulcfs,nulcfs,nulcfs,swd,'db1');
Чтобы отобразить приближение и детали на уровне 1, ввести
colormap(map)
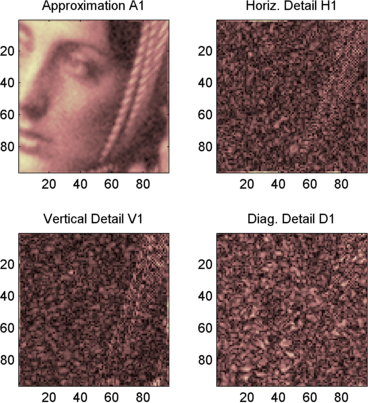
subplot(2,2,1), image(wcodemat(A1,192));
title('Approximation A1')
subplot(2,2,2), image(wcodemat(H1,192));
title('Horiz. Detail H1')
subplot(2,2,3), image(wcodemat(V1,192));
title('Vertical Detail V1')
subplot(2,2,4), image(wcodemat(D1,192));
title('Diag. Detail D1')
Выполните многоуровневое Стационарное Разложение Вейвлета.
Чтобы выполнить разложение на уровне 3 изображения (снова использующий вейвлет db1), ввести
[swa,swh,swv,swd] = swt2(X,3,'db1');
Это генерирует коэффициенты приближений на уровнях 1, 2, и 3 (swa) и коэффициенты деталей (swh, swv и swd). Заметьте, что матрицы swa(:,:,i), swh(:,:,i), swv(:,:,i) и swd(:,:,i) для данного уровня i имеют размер размера изображения. Ввод
clear A0 A1 D1 H1 V1 err nulcfs whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96x3 | 221184 | double array |
swh | 96x96x3 | 221184 | double array |
swv | 96x96x3 | 221184 | double array |
swd | 96x96x3 | 221184 | double array |
Отобразите коэффициенты приближений и деталей.
Чтобы отобразить коэффициенты приближений и деталей, ввести
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(swa(:,:,i),192));
title(['Approx. cfs level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(swh(:,:,i),192));
title(['Horiz. Det. cfs level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(swv(:,:,i),192));
title(['Vert. Det. cfs level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(swd(:,:,i),192));
title(['Diag. Det. cfs level ',num2str(i)])
kp = kp + 4;
end
Восстановите приближение на Уровне 3 и деталях от коэффициентов.
Чтобы восстановить приближение на уровне 3, ввести
mzero = zeros(size(swd)); A = mzero; A(:,:,3) = iswt2(swa,mzero,mzero,mzero,'db1');
Чтобы восстановить детали на уровнях 1, 2 и 3, ввести
H = mzero; V = mzero;
D = mzero;
for i = 1:3
swcfs = mzero; swcfs(:,:,i) = swh(:,:,i);
H(:,:,i) = iswt2(mzero,swcfs,mzero,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swv(:,:,i);
V(:,:,i) = iswt2(mzero,mzero,swcfs,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swd(:,:,i);
D(:,:,i) = iswt2(mzero,mzero,mzero,swcfs,'db1');
end
Восстановите и отобразите приближения на Уровнях 1, 2 от приближения на Уровне 3 и деталей на Уровнях 1, 2, и 3.
Чтобы восстановить приближения на уровнях 2 и 3, ввести
A(:,:,2) = A(:,:,3) + H(:,:,3) + V(:,:,3) + D(:,:,3); A(:,:,1) = A(:,:,2) + H(:,:,2) + V(:,:,2) + D(:,:,2);
Отобразить приближения и детали на уровнях 1, 2, и 3, тип
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(A(:,:,i),192));
title(['Approx. level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(H(:,:,i),192));
title(['Horiz. Det. level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(V(:,:,i),192));
title(['Vert. Det. level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(D(:,:,i),192));
title(['Diag. Det. level ',num2str(i)])
kp = kp + 4;
end
Удалите шум пороговой обработкой.
К denoise изображение используйте пороговое значение, мы находим использование инструмента приложения Wavelet Analyzer (см. следующий раздел), используйте команду wthresh, чтобы выполнить фактическую пороговую обработку коэффициентов детали, и затем использовать команду iswt2, чтобы получить изображение denoised.
thr = 44.5; sorh = 's'; dswh = wthresh(swh,sorh,thr); dswv = wthresh(swv,sorh,thr); dswd = wthresh(swd,sorh,thr); clean = iswt2(swa,dswh,dswv,dswd,'db1');
Чтобы отобразить и оригинал и изображения denoised, ввести
colormap(map)
subplot(1,2,1), image(wcodemat(X,192));
title('Original image')
subplot(1,2,2), image(wcodemat(clean,192));
title('denoised image')

Второй синтаксис может использоваться для swt2 и функций iswt2, давая те же результаты:
lev= 4; swc = swt2(X,lev,'db1'); swcden = swc; swcden(:,:,1:end-1) = wthresh(swcden(:,:,1:end-1),sorh,thr); clean = iswt2(swcden,'db1');
Вы получаете тот же график при помощи команд plot на шаге 9 выше.
В этом разделе мы исследуем стратегию изображений шумоподавления на основе 2D стационарного анализа вейвлета с помощью приложения Wavelet Analyzer. Основная идея состоит в том, чтобы составить в среднем много немного отличающихся дискретных исследований вейвлета.
Запустите стационарный вейвлет преобразовывают шумоподавление 2D инструмент.
От посдказки MATLAB введите waveletAnalyzer.
Wavelet Analyzer появляется:
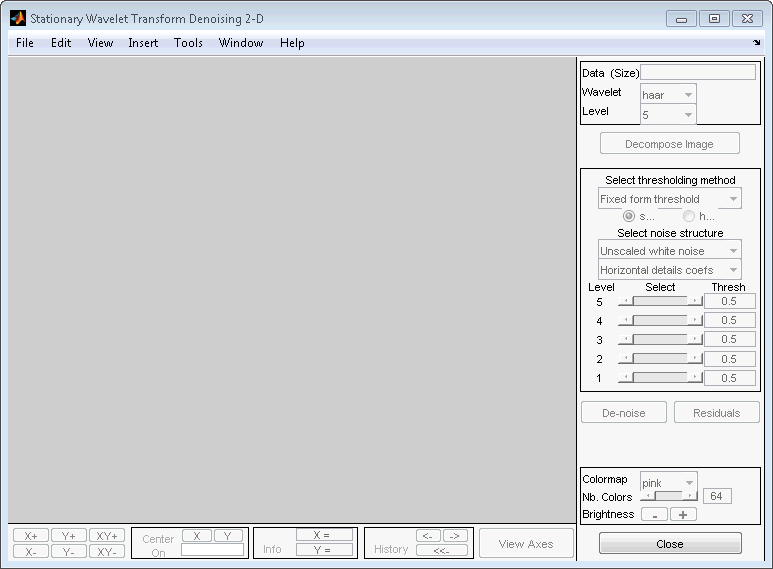
Кликните по пункту меню SWT Denoising 2-D.
Загрузка данных.
В подсказке команды MATLAB ввести
load noiswom
X. Нажмите ОК, чтобы импортировать изображение.Выполните стационарное разложение вейвлета.
Выберите вейвлет haar из меню Wavelet, выберите 4 из меню Level, и затем нажмите Decompose Image button.
Инструмент отображает гистограммы стационарных коэффициентов детали вейвлета изображения слева от окна. Эти гистограммы организованы можно следующим образом:
От нижней части для уровня 1 к верхней части для уровня 4
На левых горизонтальных коэффициентах, в средних диагональных коэффициентах, и на правильных вертикальных коэффициентах
Denoise изображение с помощью Стационарного Преобразования Вейвлета.
В то время как много опций доступны для подстройки алгоритма шумоподавления, мы примем значения по умолчанию фиксированной формы мягкая пороговая обработка и немасштабированный белый шум. Ползунки, расположенные справа от окна, управляют зависимыми порогами уровня, обозначенными пунктирными линиями, запускающимися вертикально через гистограммы коэффициентов слева от окна. Нажмите кнопку Denoise.
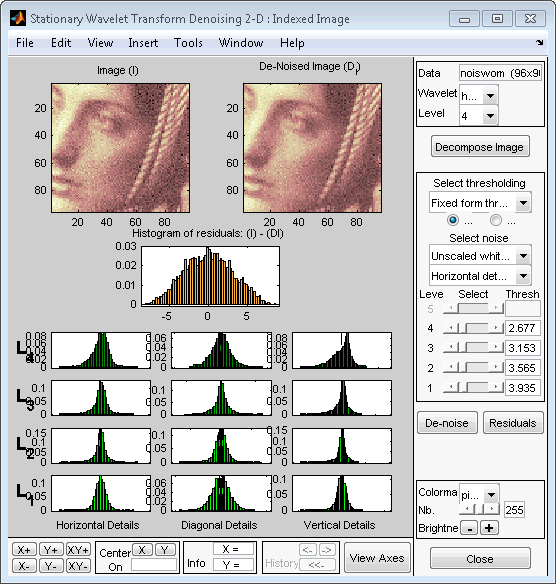
Результат, кажется, сверхсглаживается и выбранные слишком агрессивные пороги. Тем не менее, гистограмма невязок довольно хороша, поскольку это близко к Распределению Гаусса, которое является шумом, введенным, чтобы произвести анализируемое изображение noiswom.mat из части оригинального изображения woman.mat.
Выбор метода задания порога.
Из Избранного меню метода задания порога выберите Penalize низкий элемент. Связанное значение по умолчанию для режима пороговой обработки автоматически установлено в трудно; примите его. Используйте ползунок Разреженности, чтобы настроить пороговое значение близко к 45,5, и затем нажать denoise кнопку.
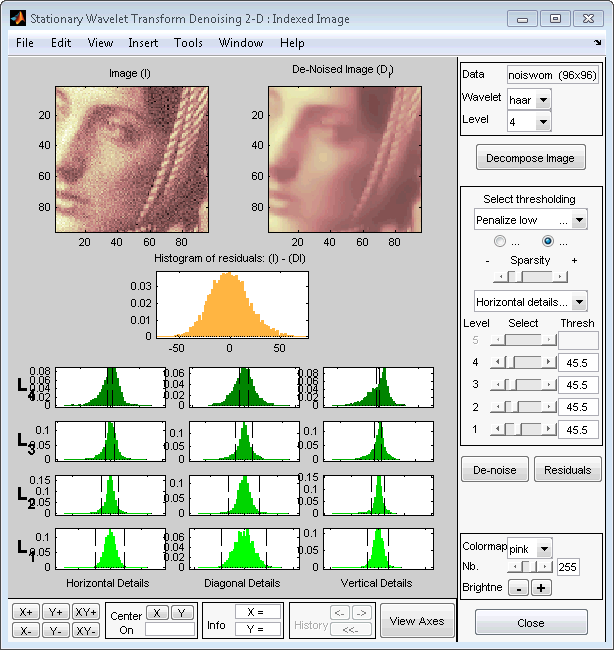
Результат является довольно удовлетворительным, несмотря на то, что возможно улучшить его немного.
Выберите вейвлет sym6 и нажмите Decompose Image button. Используйте ползунок Разреженности, чтобы настроить пороговое значение близко к 40,44, и затем нажать denoise кнопку.
Инструмент позволяет вам сохранить изображение denoised на диск. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы сохранить denoised образ от существующего процесса шумоподавления, используйте файл меню>, Сохраняют denoised Образ. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения изображения. Введите имя dnoiswom. После сохранения данных изображения к файлу dnoiswom.mat загрузите переменные в свою рабочую область:
load dnoiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
valTHR | 3x4 | 96 | double array |
wname | 1x4 | 8 | char array |
Изображением denoised является X, и map является палитрой. Кроме того, параметры процесса шумоподавления доступны. Имя вейвлета содержится в wname, и зависимые пороги уровня закодированы в valTHR. Переменная valTHR имеет четыре столбца (уровень разложения) и три строки (один для каждой ориентации детали).