Пакеты вейвлета

Пакетный метод вейвлета является обобщением разложения вейвлета, которое предлагает более богатый анализ сигнала.

Пакетные атомы вейвлета являются формами волны, индексированными тремя естественно интерпретированными параметрами: положение, шкала (как в разложении вейвлета), и частота.

Для данной ортогональной функции вейвлета мы генерируем библиотеку названных пакетных основ вейвлета основ. Каждая из этих основ предлагает конкретный способ закодировать сигналы, сохраняя глобальную энергию, и восстанавливая точные функции. Пакеты вейвлета могут использоваться для многочисленных расширений данного сигнала. Мы затем выбираем самое подходящее разложение данного сигнала относительно основанного на энтропии критерия.

Там существуйте простые и эффективные алгоритмы и для пакетного разложения вейвлета и для оптимального выбора разложения. Мы можем затем произвести адаптивные алгоритмы фильтрации с прямыми приложениями в оптимальном кодировании сигнала и сжатии данных.

От вейвлетов до пакетов вейвлета

В ортогональной процедуре разложения вейвлета типичный шаг разделяет коэффициенты приближения в две части. После разделения мы получаем вектор коэффициентов приближения и вектор коэффициентов детали, обоих в более грубой шкале. Информация, потерянная между двумя последовательными приближениями, получена в коэффициентах детали. Затем следующий шаг состоит из разделения нового вектора коэффициентов приближения; последовательные детали никогда не повторно анализируются.

В соответствующей пакетной ситуации с вейвлетом каждый вектор коэффициентов детали также разложен на две части с помощью того же подхода в качестве в разделении вектора приближения. Это предлагает самый богатый анализ: полное двоичное дерево производится как показано в следующей фигуре.

Пакетное дерево разложения вейвлета на уровне 3

Идея этого разложения состоит в том, чтобы начать с ориентированного на шкалу разложения, и затем анализировать полученные сигналы на поддиапазонах частоты.

Пакеты вейвлета в действии: введение

Следующие простые примеры иллюстрируют определенные различия между анализом вейвлета и пакетным анализом вейвлета.

Пакетный спектр вейвлета

Спектральный анализ широкого смысла стационарные сигналы с помощью преобразования Фурье известен. Для неустановившихся сигналов там существуйте локальные методы Фурье, такие как кратковременное преобразование Фурье (STFT). Смотрите Кратковременное преобразование Фурье для краткого описания.

Поскольку вейвлеты локализуются вовремя и частота, возможно использовать основанные на вейвлете дубликаты для STFT для анализа частоты времени неустановившихся сигналов. Например, возможно создать scalogram (wscalogram) на основе непрерывного вейвлета преобразовывает (CWT). Однако потенциальный недостаток использования CWT - то, что это в вычислительном отношении дорого.

Дискретный вейвлет преобразовывает (DWT) разрешает разложение частоты времени входного сигнала, но степень разрешения частоты в DWT обычно рассматривается слишком крупной для практического анализа частоты времени.

Как компромисс между DWT-и основанными на CWT методами, пакеты вейвлета предоставляют в вычислительном отношении эффективной альтернативе достаточное разрешение частоты. Можно использовать wpspectrum, чтобы выполнить анализ частоты времени сигнала с помощью пакетов вейвлета.

Следующие примеры иллюстрируют использование пакетов вейвлета, чтобы выполнить локальный спектральный анализ. Следующие примеры также используют spectrogram из программного обеспечения Signal Processing Toolbox™ как сравнительный тест, чтобы выдержать сравнение с пакетным спектром вейвлета. Если у вас нет программного обеспечения Signal Processing Toolbox, можно просто запустить пакетные примеры спектра вейвлета.

Пакетный спектр вейвлета синусоиды.

fs = 1000; % sampling rate
t = 0:1/fs:2; % 2 secs at 1kHz sample rate
y = sin(256*pi*t); % sine of period 128
level = 6;
wpt = wpdec(y,level,'sym8');
[Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');

Если у вас есть программное обеспечение Signal Processing Toolbox, можно вычислить кратковременное преобразование Фурье.

figure;
windowsize = 128;
window = hanning(windowsize);
nfft = windowsize;
noverlap = windowsize-1;
[S,F,T] = spectrogram(y,window,noverlap,nfft,fs);
imagesc(T,F,log10(abs(S)))
set(gca,'YDir','Normal')
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('Short-time Fourier Transform spectrum')

Сумма двух синусоид с частотами 64 и 128 герц.

fs = 1000;
t = 0:1/fs:2;
y = sin(128*pi*t) + sin(256*pi*t); % sine of periods 64 and 128.
level = 6;
wpt = wpdec(y,level,'sym8');
[Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');

figure;
windowsize = 128;
window = hanning(windowsize);
nfft = windowsize;
noverlap = windowsize-1;
[S,F,T] = spectrogram(y,window,noverlap,nfft,fs);
imagesc(T,F,log10(abs(S)))
set(gca,'YDir','Normal')
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('Short-time Fourier Transform spectrum')

Сигнал с резким изменением в частоте от 16 до 64 герц в две секунды.

fs = 500;
t = 0:1/fs:4;
y = sin(32*pi*t).*(t<2) + sin(128*pi*t).*(t>=2);
level = 6;
wpt = wpdec(y,level,'sym8');
[Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');

figure;
windowsize = 128;
window = hanning(windowsize);
nfft = windowsize;
noverlap = windowsize-1;
[S,F,T] = spectrogram(y,window,noverlap,nfft,fs);
imagesc(T,F,log10(abs(S)))
set(gca,'YDir','Normal')
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('Short-time Fourier Transform spectrum')

Пакетный спектр вейвлета линейного щебета.

fs = 1000;
t = 0:1/fs:2;
y = sin(256*pi*t.^2);
level = 6;
wpt = wpdec(y,level,'sym8');
[Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');

figure;
windowsize = 128;
window = hanning(windowsize);
nfft = windowsize;
noverlap = windowsize-1;
[S,F,T] = spectrogram(y,window,noverlap,nfft,fs);
imagesc(T,F,log10(abs(S)))
set(gca,'YDir','Normal')
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('Short-time Fourier Transform spectrum')

Пакетный спектр вейвлета квадратичного щебета.

y = wnoise('quadchirp',10);
len = length(y);
t = linspace(0,5,len);
fs = 1/t(2);
level = 6;
wpt = wpdec(y,level,'sym8');
[Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');

windowsize = 128;
window = hanning(windowsize);
nfft = windowsize;
noverlap = windowsize-1;
imagesc(T,F,log10(abs(S)))
set(gca,'YDir','Normal')
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('Short-time Fourier Transform spectrum')

Создание пакетов вейвлета

Схема вычисления пакетной генерации вейвлета легка при использовании ортогонального вейвлета. Мы запускаем с двух фильтров длины 2N, где h (n) и g (n), соответствуйте вейвлету.

Теперь индукцией позволяют нам задать следующую последовательность функций:

(W _n (x), n = 0, 1, 2...)

$W_{2 n} (x) = \sqrt{2} \sum_{k = 0}^{2 N - 1} h (k) W_{n} (2 x - k)$

$W_{2 n + 1} (x) = \sqrt{2} \sum_{k = 0}^{2 N - 1} g (k) W_{n} (2 x - k)$

где W ₀(x) = φ(x) является масштабирующейся функцией, и W ₁(x) = ψ(x) является функцией вейвлета.

Например, для вейвлета Хаара мы имеем

$N = 1, h (0) = h (1) = \frac{1}{\sqrt{2}}$

$g (0) = - g (1) = \frac{1}{\sqrt{2}}$

Уравнения становятся

$W_{2 n} (x) = W_{n} (2 x) + W_{n} (2 x - 1)$

$W_{2 n + 1} (x) = W_{n} (2 x) - W_{n} (2 x - 1)$

W ₀(x) = φ(x) является Хаар, масштабирующий функцию, и W ₁(x) = ψ(x) является вейвлетом Хаара, оба поддержанные в [0, 1]. Затем мы можем получить W ₂_n путем добавления два 1/2-scaled версии _Wn с отличными поддержками [0,1/2] и [1/2,1] и получить W _2n+1 путем вычитания тех же версий _Wn.

Для n = от 0 до 7, у нас есть W - функции, показанные в Пакетах Вейвлета фигуры Хаара.

Пакеты вейвлета Хаара

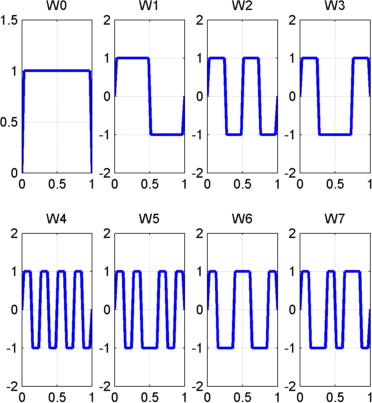
Это может быть получено с помощью следующей команды:

[wfun,xgrid] = wpfun('db1',7,5);

который возвращает в wfun приближенные значения _Wn для n = от 0 до 7, вычисленный на ^1/25 сетке поддержки xgrid.

Начиная с более регулярных исходных вейвлетов и использования подобной конструкции, мы получаем сглаживавшие версии этой системы W - функции, все с поддержкой в интервале [0, 2N–1]. Пакеты Вейвлета фигуры db2 представляют систему W - функционирует для исходного вейвлета db2.

Пакеты Вейвлета db2

Пакетные атомы вейвлета

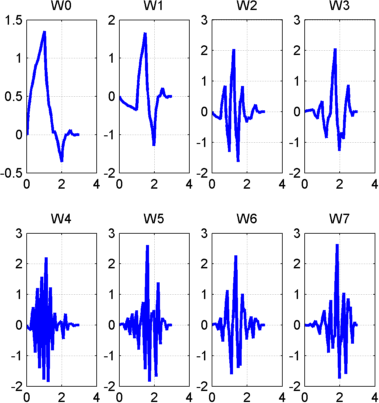
Запуск с функций $(W_{n} (x), n \in N)$ и после того же продвижения строки к ортогональным вейвлетам, мы рассматриваем трехиндексируемое семейство анализа функций (формы волны):

$(W_{j, n, k} (x) = 2^{- j / 2} W_{n} (2^{- j} x - k)$

где n ∊N и (j, k) ∊Z2.

Как в среде вейвлета, k может быть интерпретирован как параметр локализации времени и j как масштабный коэффициент. Таким образом, какова интерпретация n?

Основная идея о пакетах вейвлета состоит в том, что для фиксированных значений j и k, _Wj,n,k анализирует колебания сигнала примерно вокруг положения 2^j · k, в шкале 2^j и на различных частотах для различных допустимых значений последнего параметра n.

На самом деле, исследуя тщательно пакеты вейвлета, отображенные в Пакетах Вейвлета Хаара и db2 Пакетах Вейвлета, естественно упорядоченный _Wn для n = 0, 1..., 7, не совпадает точно с порядком, заданным количеством колебаний. Более точно, считая количество нулевых пересечений (-пересечения и вниз-пересечения) для пакетов вейвлета db1, у нас есть следующее.

Естественный порядок n	0	1	2	3	4	5	6	7
Количество нулевых пересечений для db 1 _Wn	2	3	5	4	9	8	6	7

Так, чтобы восстановить свойство, которое основная частота увеличивает монотонно с порядком, удобно задать порядок частоты, полученный из естественного рекурсивно.

Естественный порядок n	0	1	2	3	4	5	6	7
Порядок r частоты (n)	0	1	3	2	6	7	5	4

Как видно в предыдущих фигурах, _Wr ₍_n₎ (x) “колеблется” приблизительно времена n.

Чтобы анализировать сигнал (щебет Примера 2, например), лучше построить пакетные коэффициенты вейвлета, выполняющие приказ частоты от низких частот в нижней части к высоким частотам наверху, а не естественно упорядоченные коэффициенты.

При графическом выводе коэффициентов различные варианты, связанные с “Частотой” или “Естественным” выбором порядка, являются доступным использованием приложения Wavelet Analyzer.

Эти опции также доступны от режима командной строки при использовании функции wpviewcf.

Организация пакетов вейвлета

Набор функций W _{j, n} = (Wj,n,k(x),k∊Z) (j, n) пакет вейвлета. Для положительных значений целых чисел j и n, пакеты вейвлета организованы в деревьях. Дерево в Пакетах Вейвлета фигуры, Организованных в Дереве; Масштабируйтесь j Задает Глубину, и Частота n Задает Положение в Дереве, создается, чтобы дать разложение максимального уровня, равное 3. Для каждой шкалы j возможные значения параметра n 0, 1..., ^2j–1.

Пакеты вейвлета, Организованные в Дереве; Масштабируйтесь j Задает Глубину, и Частота n Задает Положение в Дереве

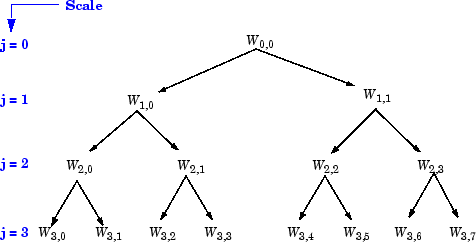
Обозначение W_j,n, где j обозначает масштабный коэффициент и n параметр частоты, сопоставимо с обычной позиционной глубиной древовидной маркировкой.

Мы имеем $W_{0, 0} = (ϕ (x - k), k \in Z)$ , и $W_{1, 1} = (ψ (\frac{x}{2} - k), k \in Z)$ .

Оказывается, что библиотека пакетных основ вейвлета содержит основание вейвлета и также несколько других основ. Давайте взглянем на некоторые из тех основ. Более точно позвольте V ₀, обозначают пробел (заполненный семейством W _0,0), в котором находится сигнал анализироваться; затем (W _d_{, 1}; d ≥ 1) является ортогональным основанием V ₀.

Для каждого строго положительного целочисленного D, (W _{D, 0}, (W _{d, 1}; 1 ≤ d ≤ D)), ортогональное основание V ₀.

Мы также знаем, что семейство функций {(_Wj _+1,2_n), (_Wj _+1,2n+1)} является ортогональным основанием пробела, заполненного _Wj,n, который разделен в два подпространства: _Wj _+1,2_n охватывает первое подпространство и _Wj _+1,2n+1 второй.

Это последнее свойство дает точную интерпретацию разделения в пакетном организационном дереве вейвлета, потому что все разработанные узлы имеют форму, показанную в Пакетном Дереве Вейвлета фигуры: Разделите и Слияние.

Пакетное дерево вейвлета: разделите и объедините

Из этого следует, что листы каждого связанного бинарного поддерева полного дерева соответствуют ортогональному основанию начального пробела.

Для конечного энергетического сигнала, принадлежащего V ₀, любое пакетное основание вейвлета обеспечит точную реконструкцию и предложит особенный метод кодирования сигнала, с помощью информационного выделения в поддиапазонах шкалы частоты.

Выбор оптимального разложения

На основе организации пакетной библиотеки вейвлета естественно считать разложения выпущенными от данного ортогонального вейвлета.

Сигнал длины, N = 2^L может быть расширен α различными способами, где α является количеством бинарных поддеревьев полного двоичного дерева глубины L. В результате $α \geq 2^{N / 2}$ (см. страницу 323 [Mal98]).

Когда этот номер может быть очень большим, и поскольку явное перечисление обычно неуправляемо, интересно найти оптимальное разложение относительно удобного критерия, вычислимого эффективным алгоритмом. Мы ищем минимум критерия.

Функции, проверяющие свойство типа аддитивности, хорошо подходят для эффективного поиска структур двоичного дерева и основного разделения. Классические основанные на энтропии критерии совпадают с этими условиями и описывают информационно-связанные свойства для точного представления данного сигнала. Энтропия является общей концепцией во многих полях, в основном в обработке сигналов. Давайте перечислим четыре различных энтропийных критерия (см. [CoiW92]); многие другие доступны и могут быть легко интегрированы (введите help wentropy). В следующих выражениях s является сигналом, и (_si) коэффициенты s в ортонормированном базисе.

Энтропийный E должен быть аддитивной функцией стоимости, таким образом что E (0) = 0 и

$E (s) = \sum_{i} E (s_{i})$

(Ненормированная) шенноновская энтропия
$E 1 (s_{i}) = - s_{i}^{2} журнал (s_{i}^{2})$
так
$E 1 (s) = - \sum_{i} s_{i}^{2} журнал (s_{i}^{2})$
с соглашением 0log (0) = 0.
Концентрация в норме ^lp с 1 ℜ ≤ p
$E 2 (s_{i}) = {| s_{i} |}^{p}$
так
$E 2 (s) = \sum_{i} {| s_{i} |}^{p} = {| s |}_{p}^{p}$
Логарифм “энергетической” энтропии
$E 3 (s_{i}) = журнал (s_{i}^{2})$
так
$E 3 (s) = \sum_{i} журнал (s_{i}^{2})$
с журналом соглашения (0) = 0.
Пороговая энтропия
$E 4 (s_{i}) = 1$ если $| s_{i} | > ε$ и 0 в другом месте, таким образом, E 4 (s) = # {i, таким образом, что $| s_{i} | > ε$ } номер моментов времени, когда сигнал больше, чем порог ε.

Эти энтропийные функции являются доступным использованием файла wentropy.

Пример 1: вычислите различные энтропии

Сгенерируйте сигнал энергии, равной 1.
```
s = ones(1,16)*0.25;
```
Вычислите шенноновскую энтропию s.
```
e1 = wentropy(s,'shannon')
    e1 = 2.7726
```
Вычислите l ^1,5 энтропии s, эквивалентного norm(s,1.5) ^1.5.
```
e2 = wentropy(s,'norm',1.5)
    e2 = 2
```
Вычислите “логарифмическую энергетическую энтропию” s.
```
e3 = wentropy(s,'log energy')
    e3 = -44.3614
```
Вычислите пороговую энтропию s с помощью порогового значения 0,24.
```
e4 = wentropy(s,'threshold', 0.24)
    e4 = 16
```

Пример 2: минимально-энтропийное разложение

Этот простой пример иллюстрирует использование энтропии, чтобы определить, представляет ли новое разделение интерес получить минимально-энтропийное разложение.

Мы запускаем с постоянного исходного сигнала. Два данных достаточны, чтобы задать и восстановить сигнал (т.е. длина и постоянное значение).
```
w00 = ones(1,16)*0.25;
```
Вычислите энтропию исходного сигнала.
```
e00 = wentropy(w00,'shannon')
    e00 = 2.7726
```
Затем разделите w00 с помощью вейвлета Хаара.
```
[w10,w11] = dwt(w00,'db1');
```
Вычислите энтропию приближения на уровне 1.
```
e10 = wentropy(w10,'shannon')
    e10 = 2.0794
```
Деталь уровня 1, w11, является нулем; энтропийный e11 является нулем. Из-за свойства аддитивности энтропия разложения дана e10+e11=2.0794. Это должно сравниться с начальным энтропийным e00=2.7726. У нас есть e10 + e11 < e00, таким образом, разделение интересно.
Теперь разделите w10 (не w11, потому что разделение пустого вектора без интереса, поскольку энтропия является нулем).
```
[w20,w21] = dwt(w10,'db1');
```
У нас есть w20=0.5*ones(1,4), и w21 является нулем. Энтропия уровня 2 приближения
```
e20 = wentropy(w20,'shannon')
    e20 = 1.3863
```
Снова у нас есть e20 + 0 < e10, таким образом разделение делает энтропийное уменьшение.
Затем
```
[w30,w31] = dwt(w20,'db1');
e30 = wentropy(w30,'shannon')
    e30 = 0.6931

[w40,w41] = dwt(w30,'db1')
    w40 = 1.0000
    w41 = 0

e40 = wentropy(w40,'shannon')
    e40 = 0
```
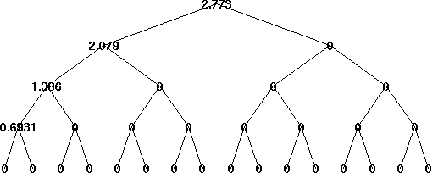
В последней операции разделения мы находим, что только одни данные необходимы, чтобы восстановить исходный сигнал. Основанием вейвлета на уровне 4 является лучшее основание согласно шенноновской энтропии (с пустой оптимальной энтропией начиная с e40+e41+e31+e21+e11 = 0).
Выполните пакетное разложение вейвлета s сигнала, заданного в примере 1.
```
t = wpdec(s,4,'haar','shannon');
```
Пакетное дерево вейвлета в Энтропийных Значениях показывает узлы, маркированные исходными энтропийными числами.
Энтропийные значения
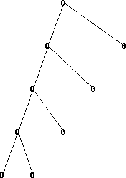
Вычислите лучшее дерево.
```
bt = besttree(t);
```
Лучшее дерево показывают в следующей фигуре. В этом случае лучшее дерево соответствует дереву вейвлета. Узлы маркированы оптимальной энтропией.
Оптимальные энтропийные значения

Некоторые интересные поддеревья

Используя вейвлет пакеты требует связанных с деревом действий и маркировки. Реализация пользовательского интерфейса создается вокруг этого фактора. Для получения дополнительной информации о технических деталях смотрите страницы с описанием.

Полное двоичное дерево глубины D, соответствующий пакетному дереву разложения вейвлета, разработанному на уровне D, обозначается WPT.

У нас есть следующие интересные поддеревья.

Дерево разложения	Поддерево, таким образом, что набором листов является основание
Пакетное дерево разложения вейвлета	Полное двоичное дерево: WPT глубины D
Пакеты вейвлета оптимальное дерево разложения	Бинарное поддерево WPT
Пакетное дерево лучшего уровня вейвлета	Завершите бинарное поддерево WPT
Дерево разложения вейвлета	Оставленное одностороннее бинарное поддерево WPT глубины D
Дерево лучшего основания вейвлета	Оставленное одностороннее бинарное поддерево WPT

Мы выводим следующие определения оптимальных разложений относительно энтропийного критерия E.

Разложения	Оптимальное разложение	Разложение лучшего уровня
Пакетные разложения вейвлета	Поиск среди 2^D деревья	Поиск среди деревьев D
Разложения вейвлета	Поиск среди деревьев D	Поиск среди деревьев D

Для любого нетерминального узла мы используем выполняющий основной шаг, чтобы найти оптимальное поддерево относительно данного энтропийного критерия E (где Eopt обозначает оптимальное энтропийное значение).

Энтропийное условие	Действие с деревом и с энтропийной маркировкой
$E (n o d e) \leq \sum_{c дочерний элемент узла} E o p t (c)$	Если (node≠root), слияние и набор Eopt (node) = E (node)
$E (n o d e) > \sum_{c дочерний элемент узла} E o p t (c)$	Разделите и установите $E o p t (n o d e) = \sum_{c дочерний элемент узла} E o p t (c)$

с естественным начальным условием на ссылочном дереве, Eopt (t) = E (t) для каждого терминального узла t.

Восстановление приближения сигнала от узла

Можно использовать функциональный wprcoef, чтобы восстановить приближение к сигналу от любого узла в пакетном дереве вейвлета. Это верно независимо от того, работаете ли вы с полным пакетным деревом вейвлета или поддеревом, определенным критерием оптимальности. Используйте wpcoef, если вы хотите извлечь пакетные коэффициенты вейвлета от узла, не восстанавливая приближение к сигналу.

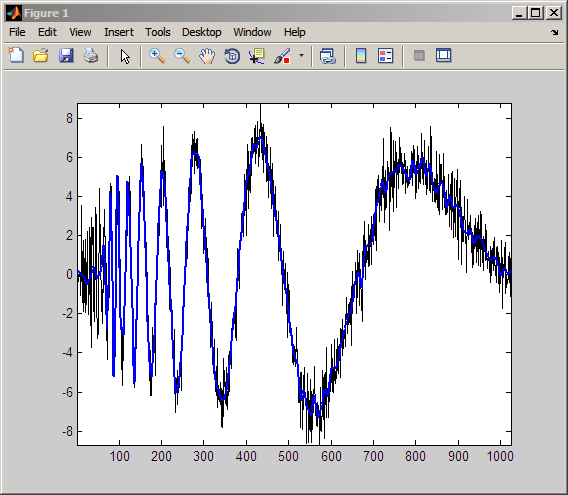
Загрузите шумный Доплеровский сигнал.

load noisdopp

Вычислите пакетное разложение вейвлета вниз к уровню 5 с помощью вейвлета sym4. Используйте periodization режим.

dwtmode('per');
T = wpdec(noisdopp,5,'sym4');
plot(T)

Постройте бинарное пакетное дерево вейвлета и нажмите (4,1) копия (узел 16).

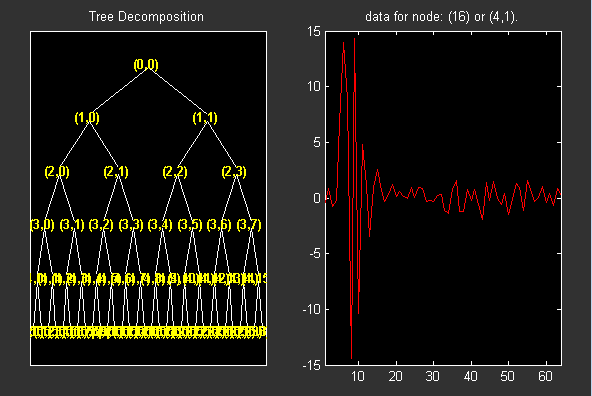
Извлеките пакетные коэффициенты вейвлета от узла 16.

wpc = wpcoef(T,16);
% wpc is length 64

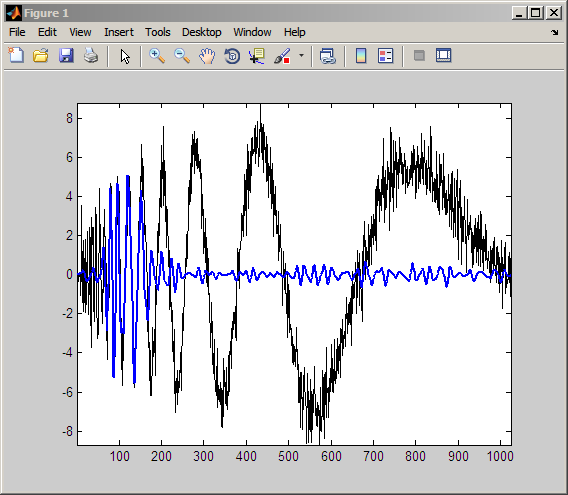
Получите приближение к сигналу от узла 16.

rwpc = wprcoef(T,16);
% rwpc is length 1024
plot(noisdopp,'k'); hold on;
plot(rwpc,'b','linewidth',2);
axis tight;

Определите оптимальное бинарное пакетное дерево вейвлета.

Topt = besttree(T);
% plot the best tree
plot(Topt)

Восстановите приближение к сигналу от (3,0) копия (узел 7).

rsig = wprcoef(Topt,7);
% rsig is length 1024
plot(noisdopp,'k'); hold on;
plot(rsig,'b','linewidth',2);
axis tight;

Если вы знаете, какую копию в бинарном пакетном дереве вейвлета вы хотите извлечь, можно определить узел, соответствующий той копии с depo2ind.

Например, чтобы определить узел, соответствующий копии (3,0), введите:

Node = depo2ind(2,[3 0]);

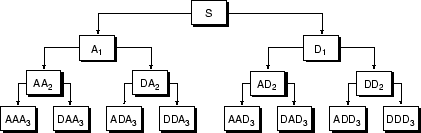
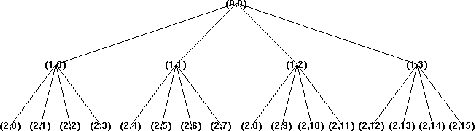
Пакеты вейвлета 2D структура разложения

Точно как в случае разложения вейвлета, предыдущая 1D среда может быть расширена к анализу изображения. Незначительные прямые модификации приводят к четверичным связанным с деревом определениям. Примеру показывают следующую фигуру для глубины 2.

Четвертичное дерево глубины 2

Пакеты вейвлета для сжатия и шумоподавления

В пакетной среде вейвлета сжатие и идеи шумоподавления идентичны разработанным в среде вейвлета. Единственной новой возможностью является более полный анализ, который обеспечивает увеличенную гибкость. Одно разложение с помощью пакетов вейвлета генерирует большое количество основ. Можно затем искать лучшее представление относительно цели проекта, с помощью besttree с энтропийной функцией.

Документация