Longitudinal Wheel

Продольное колесо с диском, барабаном или сопоставленным тормозом

Библиотека:
Powertrain Blockset / Ходовая часть / Колеса
Vehicle Dynamics Blockset / Колеса и Шины

Описание

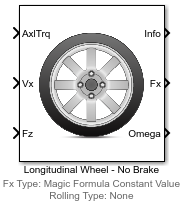
Блок Longitudinal Wheel реализует продольное поведение идеального колеса. Можно задать продольный метод расчета силы и сопротивления качению и тормозить тип. Используйте блок в автомобильной трансмиссии и продольных симуляциях транспортного средства, где низкочастотная дорога шины и тормозные усилия обязаны определять ускорение транспортного средства, торможение и сопротивление качению колеса. Например, можно использовать блок, чтобы определить крутящий момент и требования к питанию для заданного цикла диска или тормозящего события. Блок не подходит для приложений, которые требуют объединенного бокового промаха.

Существует четыре типа блоков Longitudinal Wheel. Каждый блок реализует различный тип тормоза.

Имя блока	Тормозите установку типа	Тормозите реализацию
Longitudinal Wheel - No Brake	`None`	'none'
Longitudinal Wheel - Disc Brake	`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие.
Longitudinal Wheel - Drum Brake	`Drum`	Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент.
Longitudinal Wheel - Mapped Brake	`Mapped`	Интерполяционная таблица, которая является функцией скорости колеса и примененного тормозного давления.

Модели блока продольная сила как функция колеса уменьшаются относительно дорожного покрытия. Чтобы вычислить продольную силу, задайте один из этих параметров Longitudinal Force.

Установка	Блокируйте реализацию
`Magic Formula constant value`	Волшебная Формула с постоянным коэффициентом для жесткости, формы, пика и искривления.
`Magic Formula pure longitudinal slip`	Волшебная Формула с зависимыми загрузкой коэффициентами та реализация уравнения 4. E9 до 4. E18 в Шине и Динамике аппарата.
`Mapped force`	Интерполяционная таблица, которая является функцией нормальной силы и отношения промаха колеса.

Чтобы вычислить крутящий момент сопротивления качению, задайте один из этих параметров Rolling Resistance.

Установка	Блокируйте реализацию
`None`	'none'
`Pressure and velocity`	Метод в Пошаговой Методологии Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости.
`ISO 28580`	Метод задан в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения.
`Magic Formula`	Волшебные уравнения формулы от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов.
`Mapped torque`	Интерполяционная таблица, которая является функцией нормальной силы и оси вращения продольная скорость.

Чтобы вычислить вертикальное движение, задайте один из этих параметров Vertical Motion.

Установка	Блокируйте реализацию
`None`	Блок передает прикладывавшие силы шасси непосредственно до сопротивления качению и продольных вычислений силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и затухания. Жесткость является функцией смещения боковой стены шины и давления. Затухание является функцией скорости боковой стены шины и давления.

Вращательная динамика колеса

Блок вычисляет инерционный ответ колеса, удовлетворяющего:

Потери оси
Тормозите и управляйте крутящим моментом
Утомите сопротивление качению
Оснуйте контакт через дорожный шиной интерфейс

Входной крутящий момент является суммированием прикладного крутящего момента оси, тормозного момента, и момент, являющийся результатом объединенного крутящего момента шины.

$T_{i} = T_{a} - T_{b} + T_{d}$

В настоящий момент являясь результатом объединенного крутящего момента шины, блок реализует тяговые силы колеса и сопротивление качению с динамикой первого порядка. Сопротивлению качению параметризовали постоянную времени в терминах релаксационной длины.

$T_{d} (s) = \frac{1}{\frac{| ω | R_{e}}{L_{e}} s + 1} (F_{x} R_{e} + M_{y})$

Чтобы вычислить крутящий момент сопротивления качению, можно задать один из этих параметров Rolling Resistance.

Установка	Блокируйте реализацию
`None`	Блокируйте сопротивление качению наборов, `_My`, обнулять.
`Pressure and velocity`	Блок использует метод в SAE Пошаговая Методология Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости. А именно, $M_{y} = R_{e} {a + b \| V_{x} \| + c V_{x}^{2}} {F_{z}^{β} p_{i}^{α}} \tanh (4 V_{x})$
`ISO 28580`	Блок использует метод, заданный в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения. Метод составляет нормальную загрузку, паразитную потерю и тепловые коррекции от условий испытания. А именно, $M_{y} = R_{e} (\frac{F_{z} C_{r}}{1 + K_{t} (T_{a m b} - T_{m e a s})} - F_{p l}) \tanh (ω)$
`Magic Formula`	Блок вычисляет сопротивление качению, `_My`, использование Волшебных уравнений Формулы от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов.
`Mapped torque`	Для сопротивления качению, `_My`, блок использует интерполяционную таблицу, которая является функцией нормальной силы и оси вращения продольная скорость.

Если тормоза включены, блок определяет торможение заблокированное или разблокированное условие на основе идеализированной сухой модели трения муфты. На основе условия тупика блок реализует их трение и динамические модели.

Если	Условие тупика	Модель трения	Динамическая модель
$\begin{array}{l} ω \neq \\ 0or \\ T_{S} < \| T_{i} + T_{f} - ω b \| \end{array}$	Разблокированный	$\begin{array}{l} T_{f} = T_{k} \\ где, \\ T_{k} = F_{c} R_{e f f} μ_{k} \tanh [4 (- ω_{d})] \\ T_{s} = F_{c} R_{e f f} μ_{s} \\ R_{e f f} = \frac{2 (R_{o}^{3} - R_{i}^{3})}{3 (R_{o}^{2} - R_{i}^{2})} \end{array}$	$\dot{ω} J = - ω b + T_{i} + T_{o}$
$\begin{array}{l} ω = \\ 0and \\ T_{S} \geq \| T_{i} + T_{f} - ω b \| \end{array}$	Заблокированный	$T_{f} = T_{s}$	$ω = 0$

Уравнения используют эти переменные.

ω	Скорость вращения колеса
a	Независимый от скорости компонент силы
b	Линейный скоростной компонент силы
c	Квадратичный скоростной компонент силы
_Le	Утомите релаксационную длину
J	Момент инерции
_My	Крутящий момент сопротивления качению
_Ta	Прикладной крутящий момент оси
_Tb	Тормозной момент
_Td	Объединенный крутящий момент шины
_Tf	Фрикционный крутящий момент
_Ti	Сетевой входной крутящий момент
_Tk	Кинетический фрикционный крутящий момент
_To	Сетевой выходной крутящий момент
_Ts	Статический фрикционный крутящий момент
_Fc	Прикладывавшая сила муфты
_Fx	Продольная сила, разработанная дорогой шины, взаимодействует через интерфейс должный уменьшиться
_Reff	Эффективный радиус муфты
_Ro	Кольцевой диск внешний радиус
_Ri	Кольцевой диск внутренний радиус
_Re	Эффективный радиус шины, в то время как при загрузке и при данном давлении
_Vx	Продольная скорость оси
_Fz	Транспортное средство нормальная сила
_Cr	Постоянное сопротивление качению
_Tamb	Температура окружающей среды
_Tmeas	Измеренная температура для постоянного сопротивления качению
_Fpl	Паразитная потеря силы
_Kt	Тепловой поправочный коэффициент
ɑ	Экспонента давления воздуха в шине
β	Нормальная экспонента силы
_pi	Давление воздуха в шине
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Тормоза

Диск

Если вы задаете параметр Brake Type Disc, блок реализует дисковый тормоз. Этот рисунок показывает виды сбоку и виды спереди дискового тормоза.

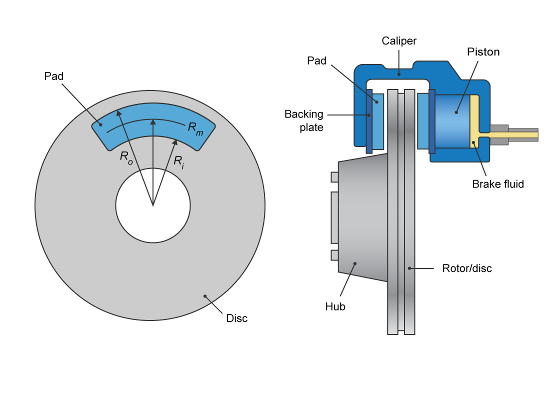
Дисковый тормоз преобразует давление в тормозном цилиндре от тормозного цилиндра в силу. Дисковый тормоз прикладывает силу в среднем радиусе тормозной колодки.

Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.

$T = {\begin{matrix} \frac{μ P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N \neq 0 \\ \frac{μ_{s t a t i c} P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N = 0 \end{matrix}$

$R m = \frac{R o + R i}{2}$

Уравнения используют эти переменные.

T	Момент привода
P	Прикладное тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в блоке дискового тормоза
_μstatic	Коэффициент ротора клавиатуры диска статического трения
μ	Коэффициент ротора клавиатуры диска кинетического трения
_Ba	Тормозите внутренний диаметр привода
_Rm	Средний радиус тормозной колодки обеспечивает приложение на тормозном роторе
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если вы задаете параметр Brake Type Drum, блок реализует статический (установившийся) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двухстороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не совместно используют общий контакт стержня.

Симплексная модель барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия обуви симметричны для обеих сторон, позволяя одному набору геометрии и параметров трения использоваться в обоих ботинках.

Блок реализует уравнения, которые выведены из этих уравнений в Основных принципах Элементов Машины.

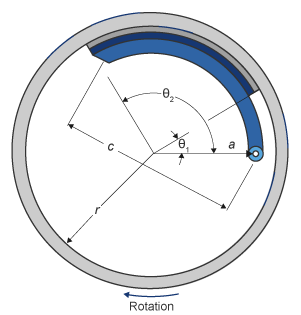
$\begin{array}{l} T_{r s h o e} = (\frac{π μ c r (потому что θ_{2} - потому что θ_{1}) B_{a}^{2}}{2 μ (2 r (потому что θ_{2} - потому что θ_{1}) + a ({потому что}^{2} θ_{2} - {потому что}^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \\ T_{l s h o e} = (\frac{π μ c r (потому что θ_{2} - потому что θ_{1}) B_{a}^{2}}{- 2 μ (2 r (потому что θ_{2} - потому что θ_{1}) + a ({потому что}^{2} θ_{2} - {потому что}^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \end{array}$

$T = {\begin{matrix} T_{r s h o e} + T_{l s h o e} когда N \neq 0 \\ (T_{r s h o e} + T_{l s h o e}) \frac{μ_{s t a t i c}}{μ} когда N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Момент привода
P	Прикладное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент ротора клавиатуры диска статического трения
μ	Коэффициент ротора клавиатуры диска кинетического трения
_Trshoe	Момент привода правого ботинка
_Tlshoe	Момент привода левого ботинка
a	Расстояние от барабана центрируется к центру контакта стержня обуви
c	Расстояние от стержня обуви прикрепляет центр, чтобы тормозить связь привода на тормозной колодке
r	Барабан внутренний радиус
_Ba	Тормозите внутренний диаметр привода
Θ1	Угол от стержня обуви прикрепляет центр, чтобы запуститься материала тормозной колодки по обуви
Θ2	Угол от стержня обуви прикрепляет центр к концу материала тормозной колодки по обуви

Сопоставленный

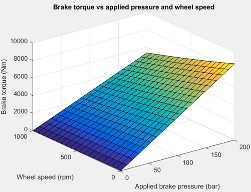
Если вы задаете параметр Brake Type Mapped, блок использует интерполяционную таблицу, чтобы определить момент привода.

$T = {\begin{matrix} f_{b r a k e} (P, N) когда N \neq 0 \\ (\frac{μ_{s t a t i c}}{μ}) f_{b r a k e} (P, N) когда N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Момент привода
$f_{b r a k e}^{} (P, N)$	Интерполяционная таблица момента привода
P	Прикладное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения поверхности клавиатуры барабана взаимодействует через интерфейс при статических условиях
μ	Коэффициент трения интерфейса ротора клавиатуры диска

Интерполяционная таблица для момента привода, $f_{b r a k e}^{} (P, N)$ , функция прикладного тормозного давления и скорости колеса, где:

T является моментом привода в N · m.
P является примененным тормозным давлением в панели.
N является скоростью колеса в об/мин.

Продольная сила

Чтобы смоделировать блок Longitudinal Wheel продольные силы, можно использовать Волшебную Формулу. Модель предоставляет установившемуся tire characteristic function F _x = f (κ, F _z), продольная сила F _x на шине, на основе:

Вертикальная загрузка F _z
Промах колеса κ

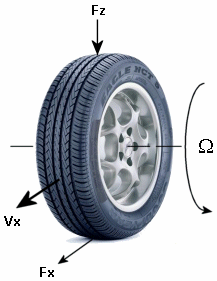
Модель Magic Formula использует эти переменные.

Ω	Скорость вращения колеса
r _w	Радиус колеса
V _x	Концентратор колеса продольная скорость
_rwΩ	Утомите шаг продольная скорость
V _sx = r _wΩ – V _x	Скорость промаха колеса
κ = V _sx / \| V _x \|	Промах колеса
F _z, F_z0	Вертикальная загрузка и номинальная вертикальная нагрузка на шину
F _x = f (κ, F _z)	Продольная сила порождена на шину в контактной точке. Также характеристическая функция f шины.

Волшебное постоянное значение формулы

Если вы устанавливаете Longitudinal Force на Magic Formula constant value, блок реализует Волшебную Формулу как определенную форму характеристической функции шины, охарактеризованной четырьмя безразмерными коэффициентами (B, C, D, E), или жесткость, форма, пик и искривление:

$F_{x} = f (κ, F_{z}) = F_{z} D sin (C \tan^{- 1} [{B κ - E [B κ - \tan^{- 1} (B κ)]}])$

Наклоном f в κ = 0 является B C D · F _z.

Коэффициенты основаны на эмпирических данных о шине. Эти значения являются типичными наборами постоянных Волшебных коэффициентов Формулы для общих дорожных условий.

Поверхность	B	C	D	E
Сухое гудронированное шоссе	10	1.9	1	0.97
Влажное гудронированное шоссе	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Волшебная формула чистый продольный промах

Если вы устанавливаете Longitudinal Force на Magic Formula pure longitudinal slip, блок реализует более общую Волшебную Формулу с помощью безразмерных коэффициентов, которые являются функциями загрузки шины. Блок реализует продольные уравнения силы в Главе 4 Шины и Динамики аппарата, включая 4. E9 до 4. E18:

$\begin{array}{l} F_{x0} = D_{} xsin (C_{x} \tan^{- 1} [{B_{x} κ_{x} - E_{x} [B_{x} κ_{x} - \tan^{- 1} (B_{x} κ_{x})]}]) + S_{Vx} \\ где: \\ κ_{x} = κ + S_{H x} \\ C_{x} = p_{C x 1} λ_{C x} \\ D_{x} = μ_{x} F_{z} ς_{1} \\ μ_{x} = (p_{D x 1} + p_{D x 2} d f_{z}) (1 + p_{p x 3} d p_{i} + p_{p x 4} d p_{i}^{2}) (1 - p_{D x 3} γ^{2}) λ^{*}_{μ x} \\ E_{x} = (p_{E x 1} + p_{E x 2} d f_{z} + p_{E x 3} d f_{z}^{2}) [1 - p_{E x 4} sgn (κ_{x})] λ_{E x} \\ K_{x κ} = F_{z} (p_{K x 1} + p_{K x 2} d f_{z}) exp (p_{Kx3} d f_{z}) (1 + p_{p x 1} d p_{i} + p_{p x 2} d p_{i}^{2}) \\ B_{x} = K_{x κ} / (C_{x} D_{x} + ε_{x}) \\ S_{H x} = p_{H x 1} + p_{H x 2} d f_{z} \\ S_{V x} = F_{z} \cdot (p_{V x 1} + p_{V x 2} d f_{z}) λ_{V x} λ^{'}_{μ x} ς_{1} \end{array}$

_SHx и _SVx представляют смещения к промаху и продольной силе в функции промаха силы, или горизонтали и вертикальным смещениям, если функция построена как кривая. _μx является зависимым продольной нагрузкой коэффициентом трения. _εx является небольшим числом, вставленным, чтобы предотвратить деление на нуль как нуль подходов _Fz.

Вертикальная динамика

Если вы не выбираете вертикальных степеней свободы установкой Vertical Motion к None, блок передает прикладывавшие силы шасси непосредственно до сопротивления качению и продольных вычислений силы.

Если вы устанавливаете Vertical Motion на Mapped stiffness and damping, вертикальное движение зависит от жесткости колеса и затухания. Жесткость является функцией смещения боковой стены шины и давления. Затухание является функцией скорости боковой стены шины и давления.

$F z t i r e (z, \dot{z}, P_{t i r e}) = F_{z k} (z, P_{t i r e}) + F_{z b} (\dot{z}, P_{t i r e})$

Блок определяет вертикальный ответ с помощью этого дифференциального уравнения.

$\ddot{z} m = F z t i r e - F_{z} - m g$

Когда вы отключаете вертикальную степень свободы, вход, нормальная сила от транспортного средства передает непосредственно продольным и прокручивающимся вычислениям силы.

$\begin{array}{l} \ddot{z} = \dot{z} = m = 0 \\ F z t i r e = m g \end{array}$

Блок использует зафиксированную колесом систему координат, чтобы разрешить вертикальные силы.

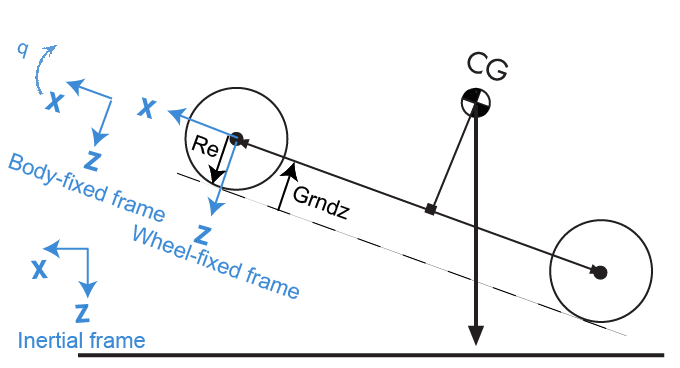
Уравнения используют эти переменные.

Fztire	Утомите нормальную силу вдоль зафиксированной колесом оси z
m	Масса оси
_Fzk	Утомите нормальную силу из-за жесткости колеса вдоль зафиксированной колесом оси z
_Fzb	Утомите нормальную силу из-за затухания колеса вдоль зафиксированной колесом оси z
_Fz	Приостановка или транспортное средство нормальная сила вдоль зафиксированной колесом оси z
_PTire	Давление воздуха в шине
$z, \dot{z}, \ddot{z}$	Утомите смещение, скорость и ускорение, соответственно, вдоль зафиксированной колесом оси z

Учет степени

Для учета степени блок реализует эти уравнения.

Сигнал шины			Описание	Уравнения
`PwrInfo`	`PwrTrnsfrd` — Степень передается между блоками Положительные сигналы указывают на поток в блок Отрицательные сигналы указывают, вытекают из блока	`PwrRoad`	Тяговое питание подано от оси	$P_{r o a d} = F_{x} V_{x}$
		`PwrAxlTrq`	Внешний крутящий момент, примененный осью к колесу	$P_{T} = T ω$
		`PwrFz`	Вертикальная сила применилась к колесу транспортным средством или приостановкой	$P_{F z} = F_{z} \dot{z}$
	`PwrNotTrnsfrd` — Степень, пересекающая контур блока, но не переданный Положительные сигналы указывают на вход Отрицательные сигналы указывают на потерю	`PwrSlip`	Тяговые потери мощности	$P_{κ} = F_{x} V_{x} + (- F_{c p} R_{e} + M_{y}) ω$
		`PwrMyRoll`	Степень сопротивления качению	$P_{M y} = M_{y} ω$
		`PwrMyBrk`	Мощность торможения	$P_{b r k} = M_{b r k} ω$
		`PwrMyb`	Прокрутка вязкой потери затухания	$P_{b} = - b ω^{2}$
		`PwrFzDamp`	Вертикальная степень затухания	$P_{F z b} = F_{z b} \dot{z}$
	`PwrStored` — Сохраненный тариф на энергоносители изменения Положительные сигналы указывают на увеличение Отрицательные сигналы указывают на уменьшение	`PwrStoredzdot`	Скорость изменения вертикальной кинетической энергии	$P_{\dot{z}} = m \ddot{z} \dot{z}$
		`PwrStoredq`	Скорость изменения вращательной кинетической энергии	$P_{ω} = I_{y y} \dot{ω} ω$
		`PwrStoredFsFzSprng`	Скорость изменения сохраненной потенциальной энергии боковой стены	$P_{F z k} = F_{z k} {\dot{z}}_{x}$
		`PwrStoredGrvty`	Скорость изменения гравитационной потенциальной энергии	$P_{g} = - m g \dot{Z}$

Уравнения используют эти переменные.

ω	Скорость вращения колеса
b	Линейный скоростной компонент силы
_Fx	Продольная сила, разработанная дорогой шины, взаимодействует через интерфейс должный уменьшиться
_Fcp	Утомите силу промаха в закрашенной фигуре контакта
_Fz	Транспортное средство нормальная сила
_Fzb	Утомите нормальную силу из-за затухания колеса
_Fzk	Утомите нормальную силу из-за жесткости колеса
_Iyy	Колесо вращательная инерция
_Mbrk	Торможение момента
_My	Крутящий момент сопротивления качению
_Re	Эффективный радиус шины, в то время как при загрузке и при данном давлении
T	Крутящий момент оси применяется на колесо
_Vx	Продольная скорость оси
$z, \dot{z}, \ddot{z}$	Утомите смещение, скорость и ускорение, соответственно
ω	Скорость вращения колеса
$\dot{Z}$	Транспортное средство вертикальная скорость вдоль зафиксированной транспортным средством оси z

Порты

Входной параметр

развернуть все

`BrkPrs` — Тормозное давление
`scalar`

Тормозное давление, в Па.

Зависимости

Чтобы создать этот порт, для параметра Brake Type, задают один из этих типов:

Disc
Drum
Mapped

`AxlTrq` — Крутящий момент оси
`scalar`

Крутящий момент оси, _Ta, об оси вращения колеса, в N · m.

`Vx` — Скорость
`scalar`

Ось продольная скорость вдоль транспортного средства (тело) - зафиксированная ось X, в m/s.

`Fz` — Нормальная сила
`scalar`

Абсолютное значение приостановки или транспортного средства нормальная сила вдоль зафиксированной телом оси z, в N.

`Gnd` — Оснуйте смещение
`scalar`

Оснуйте смещение, Grndz, вдоль отрицательной зафиксированной колесом оси z, в m.

Зависимости

Создать Gnd:

Установите Vertical Motion на Mapped stiffness and damping.
На панели Vertical выберите Input ground displacement.

`lam_mux` — Масштабный коэффициент трения
`scalar`

Продольный масштабный коэффициент трения, безразмерный.

Зависимости

Чтобы создать этот порт, выберите Input friction scale factor.

`TirePrs` — Давление воздуха в шине
`scalar`

Давление воздуха в шине, в Па.

Зависимости

Создать этот порт:

Установите один из этих параметров:
- Longitudinal Force к Magic Formula pure longitudinal slip.
- Rolling Resistance к Pressure and velocity или Magic Formula.
- Vertical Motion к Mapped stiffness and damping.
На панели Wheel Dynamics выберите Input tire pressure.

`Tamb` — Температура окружающей среды
`scalar`

Температура окружающей среды, _Tamb, в K.

Зависимости

Создать этот порт:

Установите Rolling Resistance на ISO 28580.
На панели Rolling Resistance выберите к Input ambient temperature.

Вывод

развернуть все

`Info` — Сигнал шины
шина

Сигнал шины, содержащий эти вычисления блока.

Сигнал			Описание	Модули
`AxlTrq`			Крутящий момент оси о зафиксированной телом оси Y	N·
`Omega`			Скорость вращения колеса о зафиксированной телом оси Y	rad/s
`Omegadot`			Колесо угловое ускорение о зафиксированной телом оси Y	rad/s^2
`Fx`			Продольная сила транспортного средства вдоль зафиксированной телом оси X	N
`Fz`			Вертикальная сила транспортного средства вдоль зафиксированной телом оси z	N
`Fzb`			Утомите нормальную силу из-за затухания колеса вдоль зафиксированной колесом оси z	N
`Fzk`			Утомите нормальную силу из-за жесткости колеса вдоль зафиксированной колесом оси z	N
`My`			Крутящий момент сопротивления качению о зафиксированной телом оси Y	N·
`Myb`			Крутящий момент сопротивления качению из-за затухания о зафиксированной телом оси Y	N·
`Kappa`			Подсуньте отношение	Нет данных
`Vx`			Транспортное средство продольная скорость вдоль зафиксированной телом оси X	m/s
`Re`			Колесо эффективный радиус вдоль зафиксированной колесом оси z	m
`BrkTrq`			Момент привода о зафиксированной телом оси Y	N·
`BrkPrs`			Тормозное давление	Па
`z`			Колесо вертикальное отклонение вдоль зафиксированной колесом оси z	m
`zdot`			Колесо вертикальная скорость вдоль зафиксированной колесом оси z	m/s
`zddot`			Колесо вертикальное ускорение вдоль зафиксированной колесом оси z	м/с^2
`Gndz`			Оснуйте смещение вдоль отрицания зафиксированной колесом оси z (положительный вход производит лифт колеса),	m
`GndFz`			Вертикальная сила колеса на земле вдоль отрицания зафиксированной колесом оси z	N
`TirePrs`			Давление воздуха в шине	Па
`Fpatch`			Тяговое питание подано от оси
`PwrInfo`	`PwrTrnsfrd`	`PwrRoad`	Внешний крутящий момент, примененный осью к колесу	W
		`PwrAxlTrq`	Вертикальная сила применилась к колесу транспортным средством или приостановкой	W
		`PwrFz`	Тяговые потери мощности	W
	`PwrNotTrnsfrd`	`PwrSlip`	Степень сопротивления качению	W
		`PwrMyRoll`	Мощность торможения	W
		`PwrMyBrk`	Прокрутка вязкой потери затухания	W
		`PwrMyb`	Вертикальная степень затухания	W
		`PwrFzDamp`	Скорость изменения вертикальной кинетической энергии	W
	`PwrStored`	`PwrStoredzdot`	Скорость изменения вращательной кинетической энергии	W
		`PwrStoredq`	Скорость изменения сохраненной потенциальной энергии боковой стены	W
		`PwrStoredFsFzSprng`	Скорость изменения гравитационной потенциальной энергии	W
		`PwrStoredGrvty`	Тяговое питание подано от оси	W

`Fx` — Продольная сила оси
`scalar`

Продольная сила, действующая на ось, вдоль зафиксированной телом оси X, в N. Положительная сила действует, чтобы переместить транспортное средство вперед.

`Omega` — Скорость вращения колеса
`scalar`

Скорость вращения колеса, о зафиксированной телом оси Y, в rad/s.

`z` — Колесо вертикальное отклонение
`scalar`

Колесо вертикальное отклонение вдоль зафиксированной колесом оси z, в m.

Зависимости

Чтобы создать этот порт, установите Vertical Motion на Mapped stiffness and damping.

`zdot` — Колесо вертикальная скорость
`scalar`

Колесо вертикальная скорость вдоль зафиксированной колесом оси z, в m/s.

Зависимости

Чтобы создать этот порт, установите Vertical Motion на Mapped stiffness and damping.

Параметры

развернуть все

Блокируйте опции

`Longitudinal Force` — Выберите тип
`Magic Formula constant value` (значение по умолчанию) | `Magic Formula pure longitudinal slip` | `Mapped force`

Установка	Блокируйте реализацию
`Magic Formula constant value`	Волшебная Формула с постоянным коэффициентом для жесткости, формы, пика и искривления.
`Magic Formula pure longitudinal slip`	Волшебная Формула с зависимыми загрузкой коэффициентами та реализация уравнения 4. E9 до 4. E18 в Шине и Динамике аппарата.
`Mapped force`	Интерполяционная таблица, которая является функцией нормальной силы и отношения промаха колеса.

Зависимости

Выбор Включает эти параметры

Выбор	Включает эти параметры
`Magic Formula constant value`	Pure longitudinal peak factor, Dx Pure longitudinal shape factor, Cx Pure longitudinal stiffness factor, Bx Pure longitudinal curvature factor, Ex
`Magic Formula pure longitudinal slip`	Cfx shape factor, PCX1 Longitudinal friction at nominal normal load, PDX1 Frictional variation with load, PDX2 Frictional variation with camber, PDX3 Longitudinal curvature at nominal normal load, PEX1 Variation of curvature factor with load, PEX2 Variation of curvature factor with square of load, PEX3 Longitudinal curvature factor with slip, PEX4 Longitudinal slip stiffness at nominal normal load, PKX1 Variation of slip stiffness with load, PKX2 Slip stiffness exponent factor, PKX3 Horizontal shift in slip ratio at nominal normal load, PHX1 Variation of horizontal slip ratio with load, PHX2 Vertical shift in load at nominal normal load, PVX1 Variation of vertical shift with load, PVX2 Linear variation of longitudinal slip stiffness with tire pressure, PPX1 Quadratic variation of longitudinal slip stiffness with tire pressure, PPX2 Linear variation of peak longitudinal friction with tire pressure, PPX3 Quadratic variation of peak longitudinal friction with tire pressure, PPX4 Linear variation of longitudinal slip stiffness with tire pressure, PPX1 Slip speed decay function scaling factor, lam_muV Brake slip stiffness scaling factor, lam_Kxkappa Longitudinal shape scaling factor, lam_Cx Longitudinal curvature scaling factor, lam_Ex Longitudinal horizontal shift scaling factor, lam_Hx Longitudinal vertical shift scaling factor, lam_Vx
`Mapped force`	Slip ratio breakpoints, kappaFx Normal force breakpoints, FzFx Longitudinal force map, FxMap

Magic Formula constant value

Pure longitudinal peak factor, Dx

Pure longitudinal shape factor, Cx

Pure longitudinal stiffness factor, Bx

Pure longitudinal curvature factor, Ex

Magic Formula pure longitudinal slip

Cfx shape factor, PCX1

Longitudinal friction at nominal normal load, PDX1

Frictional variation with load, PDX2

Frictional variation with camber, PDX3

Longitudinal curvature at nominal normal load, PEX1

Variation of curvature factor with load, PEX2

Variation of curvature factor with square of load, PEX3

Longitudinal curvature factor with slip, PEX4

Longitudinal slip stiffness at nominal normal load, PKX1

Variation of slip stiffness with load, PKX2

Slip stiffness exponent factor, PKX3

Horizontal shift in slip ratio at nominal normal load, PHX1

Variation of horizontal slip ratio with load, PHX2

Vertical shift in load at nominal normal load, PVX1

Variation of vertical shift with load, PVX2

Linear variation of longitudinal slip stiffness with tire pressure, PPX1

Quadratic variation of longitudinal slip stiffness with tire pressure, PPX2

Linear variation of peak longitudinal friction with tire pressure, PPX3

Quadratic variation of peak longitudinal friction with tire pressure, PPX4

Linear variation of longitudinal slip stiffness with tire pressure, PPX1

Slip speed decay function scaling factor, lam_muV

Brake slip stiffness scaling factor, lam_Kxkappa

Longitudinal shape scaling factor, lam_Cx

Longitudinal curvature scaling factor, lam_Ex

Longitudinal horizontal shift scaling factor, lam_Hx

Longitudinal vertical shift scaling factor, lam_Vx

Mapped force

Slip ratio breakpoints, kappaFx

Normal force breakpoints, FzFx

Longitudinal force map, FxMap

`Rolling Resistance` — Выберите тип
`None` (значение по умолчанию) | `Pressure and velocity` | `ISO 28580` | `Magic Formula` | `Mapped torque`

Чтобы вычислить крутящий момент сопротивления качению, задайте один из этих параметров Rolling Resistance.

Установка	Блокируйте реализацию
`None`	'none'
`Pressure and velocity`	Метод в Пошаговой Методологии Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости.
`ISO 28580`	Метод задан в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения.
`Magic Formula`	Волшебные уравнения формулы от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов.
`Mapped torque`	Интерполяционная таблица, которая является функцией нормальной силы и оси вращения продольная скорость.

Зависимости

Выбор	Параметры
`Pressure and velocity`	Velocity independent force coefficient, aMy Linear velocity force component, bMy Quadratic velocity force component, cMy Tire pressure exponent, alphaMy Normal force exponent, betaMy
`ISO 28580`	Parasitic losses force, Fpl Rolling resistance constant, Cr Thermal correction factor, Kt Measured temperature, Tmeas Parasitic losses force, Fpl Ambient temperature, Tamb
`Magic Formula`	Rolling resistance torque coefficient, QSY Longitudinal force rolling resistance coefficient, QSY2 Linear rotational speed rolling resistance coefficient, QSY3 Quartic rotational speed rolling resistance coefficient, QSY4 Camber squared rolling resistance torque, QSY5 Load based camber squared rolling resistance torque, QSY6 Normal load rolling resistance coefficient, QSY7 Pressure load rolling resistance coefficient, QSY8 Rolling resistance scaling factor, lam_My
`Mapped torque`	Spin axis velocity breakpoints, VxMy Normal force breakpoints, FzMy Rolling resistance torque map, MyMap

`Brake Type` — Выберите тип
`None` | `Disc` | `Drum` | `Mapped`

Существует четыре типа блоков Longitudinal Wheel. Каждый блок реализует различный тип тормоза.

Имя блока	Тормозите установку типа	Тормозите реализацию
Longitudinal Wheel - No Brake	`None`	'none'
Longitudinal Wheel - Disc Brake	`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие.
Longitudinal Wheel - Drum Brake	`Drum`	Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент.
Longitudinal Wheel - Mapped Brake	`Mapped`	Интерполяционная таблица, которая является функцией скорости колеса и примененного тормозного давления.

`Vertical Motion` — Выберите тип
`None` (значение по умолчанию) | `Mapped stiffness and damping`

Чтобы вычислить вертикальное движение, задайте один из этих параметров Vertical Motion.

Установка	Блокируйте реализацию
`None`	Блок передает прикладывавшие силы шасси непосредственно до сопротивления качению и продольных вычислений силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и затухания. Жесткость является функцией смещения боковой стены шины и давления. Затухание является функцией скорости боковой стены шины и давления.

Выбор Включает эти параметры Создает эти выходные порты

Выбор	Включает эти параметры	Создает эти выходные порты
`Mapped stiffness and damping`	Wheel and unsprung mass, m Initial deflection, zo Initial velocity, zdoto Gravitational acceleration, g Vertical deflection breakpoints, zFz Pressure breakpoints, pFz Force due to deflection, Fzz Vertical velocity breakpoints, zdotFz Force due to velocity, Fzzdot Ground displacement, Gndz Input ground displacement	`z` `zdot`

Mapped stiffness and damping

Wheel and unsprung mass, m

Initial deflection, zo

Initial velocity, zdoto

Gravitational acceleration, g

Vertical deflection breakpoints, zFz

Pressure breakpoints, pFz

Force due to deflection, Fzz

Vertical velocity breakpoints, zdotFz

Force due to velocity, Fzzdot

Ground displacement, Gndz

Input ground displacement

z

zdot

`Longitudinal scaling factor, lam_x` — Масштабный коэффициент трения
1 (значение по умолчанию)

Продольный масштабный коэффициент трения, безразмерный.

Зависимости

Чтобы включить этот параметр, очистите Input friction scale factor.

`Input friction scale factor` — Выбор
`Off` (значение по умолчанию)

Создайте входной порт для продольного масштабного коэффициента трения.

Зависимости

Выбор этого параметра:

Создает входной порт lam_mux.
Отключает параметр Longitudinal scaling factor, lam_x.

Динамика колеса

`Axle viscous damping coefficient, br` — Затухание
`scalar`

Ось вязкий коэффициент затухания, br, в N · m·.

`Wheel inertia, Iyy` — Инерция
`scalar`

Инерция колеса, в kg · м^2.

`Wheel initial angular velocity, omegao` — Скорость колеса
`scalar`

Начальная скорость вращения колеса, вдоль зафиксированной телом оси Y, в rad/s.

`Relaxation length, Lrel` — Релаксационная длина
`scalar`

Продолжительность релаксации колеса, в m.

`Loaded radius, Re` — Загруженный радиус
`scalar`

Загруженный радиус колеса, Re, в m.

`Unloaded radius, UNLOADED_RADIUS` — Разгруженный радиус
`scalar`

Разгруженный радиус колеса, в m.

Зависимости

Чтобы создать этот параметр, установите Rolling Resistance на Pressure and velocity или Magic Formula.

`Nominal longitudinal speed, LONGVL` — Скорость
`scalar`

Номинальная продольная скорость вдоль зафиксированной телом оси X, в m/s.

Зависимости

Чтобы включить этот параметр, установите Longitudinal Force на Magic Formula pure longitudinal slip.

`Nominal camber angle, gamma` — Изгиб
`scalar`

Номинальный угол изгиба, в рад.

Зависимости

Чтобы включить этот параметр, установите также:

Longitudinal Force к Magic Formula pure longitudinal slip.
Rolling Resistance к Magic Formula.

`Nominal pressure, NOMPRES` — Давление
`scalar`

Номинальное давление, в Па.

Зависимости

Чтобы включить этот параметр, установите также:

Longitudinal Force к Magic Formula pure longitudinal slip.
Rolling Resistance к Magic Formula.

`Pressure, press` — Давление
`scalar`

Давление, в Па.

Зависимости

Включить этот параметр:

Установите один из них:
- Longitudinal Force к Magic Formula pure longitudinal slip.
- Rolling Resistance к Pressure and velocity или Magic Formula.
- Vertical Motion к Mapped stiffness and damping.
На панели Wheel Dynamics очистите Input tire pressure.

Продольный

Волшебное постоянное значение формулы

`Pure longitudinal peak factor, Dx` фактор
`scalar`

Чистый продольный пиковый фактор, безразмерный.

Поверхность	B	C	D	E
Сухое гудронированное шоссе	10	1.9	1	0.97
Влажное гудронированное шоссе	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal shape factor, Cx` фактор
`scalar`

Чистый продольный масштабный фактор, безразмерный.

Поверхность	B	C	D	E
Сухое гудронированное шоссе	10	1.9	1	0.97
Влажное гудронированное шоссе	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal stiffness factor, Bx` фактор
`scalar`

Чистый продольный фактор жесткости, безразмерный.

Поверхность	B	C	D	E
Сухое гудронированное шоссе	10	1.9	1	0.97
Влажное гудронированное шоссе	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal curvature factor, Ex` фактор
`scalar`

Чистый продольный фактор искривления, безразмерный.

Поверхность	B	C	D	E
Сухое гудронированное шоссе	10	1.9	1	0.97
Влажное гудронированное шоссе	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.