Компенсируйте смещение несущей частоты
comm.CarrierSynchronizer Система object™ компенсирует несущую частоту и смещения фазы в сигналах что схемы модуляции одно поставщика услуг использования. Алгоритм синхронизатора поставщика услуг совместим с BPSK, QPSK, OQPSK, 8-PSK, PAM и прямоугольными схемами модуляции QAM.
Этот Системный объект не разрешает неоднозначности фазы, созданные алгоритмом синхронизации. Как обозначено в этой таблице, потенциальная неоднозначность фазы, введенная синхронизатором, зависит от типа модуляции:
| Модуляция | Неоднозначность фазы (степени) |
|---|---|
'BPSK' или 'PAM' | 0, 180 |
'OQPSK', 'QPSK', или 'QAM' | 0, 90, 180, 270 |
'8PSK' | 0, 45, 90, 135, 180, 225, 270, 315 |
Примеры демонстрируют синхронизацию поставщика услуг и разрешение неоднозначности фазы.
Для лучших результатов примените синхронизацию поставщика услуг к несверхдискретизированным сигналам, как продемонстрировано в Правильном Смещении Фазы и Частоты для 16-QAM Используя Крупную и Прекрасную Синхронизацию.
Компенсировать частоту и фазу возмещает в сигналах что схемы модуляции одно поставщика услуг использования:
Создайте comm.CarrierSynchronizer объект и набор его свойства.
Вызовите объект, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты? MATLAB.
carrSynch = comm.CarrierSynchronizer
carrSynch = comm.CarrierSynchronizer(Name,Value)
Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Правильная фаза и смещения частоты сигнала QPSK прошли через канал AWGN. Используя преамбулы, устраните неоднозначность фазы.
Задайте параметры симуляции.
M = 4; % Modulation order rng(1993) % For repeatable results barker = comm.BarkerCode(... 'Length',13,'SamplesPerFrame',13); % For preamble msgLen = 1e4; numFrames = 10; frameLen = msgLen/numFrames;
Добавьте преамбулы в каждую систему координат, которые используются позже при выполнении разрешения неоднозначности фазы. Сгенерируйте случайные символы данных и примените модуляцию QPSK.
preamble = (1+barker())/2; % Length 13, unipolar data = zeros(msgLen,1); for idx = 1 : numFrames payload = randi([0 M-1],frameLen-barker.Length,1); data((idx-1)*frameLen + (1:frameLen)) = [preamble; payload]; end modSig = pskmod(data,4,pi/4);
Создайте comm.PhaseFrequencyOffset Система object™, чтобы ввести фазу и частоту возмещает к модулируемому входному сигналу. Установите смещение фазы к 45 степени, смещение частоты к 1 кГц и частота дискретизации к 10 кГц. Смещение частоты установлено в 1% частоты дискретизации.
pfo = comm.PhaseFrequencyOffset('PhaseOffset',45, ... 'FrequencyOffset',1e4,'SampleRate',1e6);
Создайте Системный объект синхронизатора поставщика услуг, чтобы использовать в исправлении фазы и смещений частоты с выборками на набор символов к 1.
carrierSync = comm.CarrierSynchronizer( ... 'SamplesPerSymbol',1,'Modulation','QPSK');
Примените фазу и смещения частоты с помощью pfo Системный объект, и затем передает сигнал через канал AWGN, чтобы добавить белый Гауссов шум.
modSigOffset = pfo(modSig); rxSig = awgn(modSigOffset,12);
Отобразите график рассеивания полученного сигнала. Данные появляются в кругу вместо того, чтобы быть сгруппированными вокруг ссылочных точек созвездия из-за смещения частоты.
scatterplot(rxSig)
Используйте carrierSync Системный объект, чтобы откорректировать фазу и смещение частоты в полученном сигнале.
syncSignal = carrierSync(rxSig);
Используйте сигнальное созвездие, чтобы отобразить первые и последние 1000 символов синхронизируемого сигнала. Перед сходимостью цикла синхронизатора нанесенные на график символы не сгруппированы вокруг ссылочных точек совокупности. После сходимости нанесенные на график символы сгруппированы вокруг ссылочных точек совокупности.
constDiag = comm.ConstellationDiagram( ... 'SymbolsToDisplaySource','Property','SymbolsToDisplay',300, ... 'ChannelNames',{'Before convergence','After convergence'},'ShowLegend',true, ... 'Position',[400 400 400 400]); constDiag([syncSignal(1:1000) syncSignal(9001:10000)]);
Демодулируйте синхронизируемый сигнал. Вычислите и отобразите общие битовые ошибки и BER.
syncData = pskdemod(syncSignal,4,pi/4); [syncDataTtlErr,syncDataBER] = biterr(data(6000:end),syncData(6000:end))
syncDataTtlErr = 3990
syncDataBER = 0.4986
Неоднозначность фазы в полученной силе сигнала вызывает битовые ошибки. Используя преамбулу, определите неоднозначность фазы. Удалите эту неоднозначность фазы из синхронизируемого сигнала уменьшать битовые ошибки.
idx = 9000 + (1:barker.Length); phOffset = angle(modSig(idx) .* conj(syncSignal(idx))); phOffset = round((2/pi) * phOffset); % -1, 0, 1, +/-2 phOffset(phOffset==-2) = 2; % Prep for mean operation phOffset = mean((pi/2) * phOffset); % -pi/2, 0, pi/2, or pi disp(['Estimated mean phase offset = ',num2str(phOffset*180/pi),' degrees'])
Estimated mean phase offset = 180 degrees
resPhzSig = exp(1i*phOffset) * syncSignal;
Демодулируйте сигнал после решения неоднозначности фазы. Повторно вычислите и отобразите обновленные общие битовые ошибки и BER. Удаление неоднозначности фазы уменьшает BER существенно.
resPhzData = pskdemod(resPhzSig,4,pi/4); [resPhzTtlErr, resPhzBER] = biterr(data(6000:end),resPhzData(6000:end))
resPhzTtlErr = 403
resPhzBER = 0.0504
Оцените смещение частоты, введенное в шумный сигнал 8-PSK использование Системы синхронизатора поставщика услуг object™.
Задайте параметры симуляции.
M = 8; % Modulation order fs = 1e6; % Sample rate (Hz) foffset = 1000; % Frequency offset (Hz) phaseoffset = 15; % Phase offset (deg) snrdb = 20; % Signal-to-noise ratio (dB)
Создайте comm.PhaseFrequencyOffset Системный объект, чтобы ввести фазу и частоту возмещает к модулируемому сигналу.
pfo = comm.PhaseFrequencyOffset('PhaseOffset',phaseoffset, ... 'FrequencyOffset',foffset,'SampleRate',fs);
Создайте Системный объект синхронизатора поставщика услуг, чтобы использовать в исправлении смещения частоты и фаза. Установите Modulation свойство к 8PSK.
carrierSync = comm.CarrierSynchronizer('Modulation','8PSK');
Сгенерируйте случайные данные и примените модуляцию 8-PSK.
data = randi([0 M-1],5000,1); modSig = pskmod(data,M,pi/M);
Примените фазу и смещения частоты с помощью pfo Системного объекта, и передайте сигнал через канал AWGN, чтобы добавить Гауссов белый шум.
modSigOffset = pfo(modSig); rxSig = awgn(modSigOffset,snrdb);
Используйте синхронизатор поставщика услуг, чтобы оценить смещение фазы полученного сигнала.
[~,phError] = carrierSync(rxSig);
Определите смещение частоты при помощи diff функция, чтобы вычислить аппроксимативную производную ошибки фазы. Производная должна масштабироваться потому что ошибка фазы измеряется в радианах.
estFreqOffset = diff(phError)*fs/(2*pi);
Постройте рабочее среднее значение предполагаемого смещения частоты. После того, как синхронизатор сходится к решению, среднее значение оценки приблизительно равно входному значению смещения частоты 1 000 Гц.
rmean = cumsum(estFreqOffset)./(1:length(estFreqOffset))'; plot(rmean) xlabel('Symbols') ylabel('Estimated Frequency Offset (Hz)') grid
Компенсация значительной фазы и смещений частоты для 16-QAM сигнала в канале AWGN выполняется на двух шагах. Во-первых, откорректируйте крупное смещение частоты с помощью оценки, обеспеченной крупным компенсатором частоты, и затем подстройте коррекцию с помощью синхронизации поставщика услуг. Из-за крупной коррекции частоты синхронизатор поставщика услуг сходится быстро даже при том, что нормированная пропускная способность установлена в низкую стоимость. Ниже нормированные значения пропускной способности включают лучшую коррекцию для маленьких остаточных смещений поставщика услуг. После применения фазы и частоты возмещает коррекции к полученному сигналу, неоднозначность фазы твердости с помощью преамбул.
Задайте параметры симуляции.
fs = 10000; % Sample rate (Hz) sps = 4; % Samples per symbol M = 16; % Modulation order k = log2(M); % Bits per symbol rng(1996) % Set seed for repeatable results barker = comm.BarkerCode(... 'Length',13,'SamplesPerFrame',13); % For preamble msgLen = 1e4; numFrames = 10; frameLen = msgLen/numFrames;
Сгенерируйте полезные нагрузки данных и добавьте преамбулу в каждую систему координат. Преамбула позже используется в разрешении неоднозначности фазы.
preamble = (1+barker())/2; % Length 13, unipolar data = zeros(msgLen, 1); for idx = 1 : numFrames payload = randi([0 M-1],frameLen-barker.Length,1); data((idx-1)*frameLen + (1:frameLen)) = [preamble; payload]; end
Создайте Системный объект для фильтрации формы импульса передачи, получить импульсной фильтрации формы, крупной компенсации частоты QAM, синхронизации поставщика услуг и схемы созвездия.
txFilter = comm.RaisedCosineTransmitFilter( ... 'OutputSamplesPerSymbol',sps); rxFilter = comm.RaisedCosineReceiveFilter(... 'InputSamplesPerSymbol',sps,'DecimationFactor',sps); coarse = comm.CoarseFrequencyCompensator('SampleRate',fs, ... 'FrequencyResolution',10); fine = comm.CarrierSynchronizer( ... 'DampingFactor',0.4,'NormalizedLoopBandwidth',0.001, ... 'SamplesPerSymbol',1,'Modulation','QAM'); axislimits = [-6 6]; constDiagram = comm.ConstellationDiagram('ReferenceConstellation',qammod(0:M-1,M), ... 'ChannelNames',{'Before convergence','After convergence'}, ... 'ShowLegend',true,'XLimits',axislimits,'YLimits',axislimits);
Также создайте Системный объект для канала AWGN, и фазу и смещение частоты, чтобы добавить нарушения в сигнал. Смещение фазы, больше, чем 90 градусов, добавляется, чтобы вызвать неоднозначность фазы, которая приводит к сдвигу квадранта созвездия.
ebn0 = 8; freqoffset = 110; phaseoffset = 110; awgnChannel = comm.AWGNChannel('EbNo',ebn0, ... 'BitsPerSymbol',k,'SamplesPerSymbol',sps); pfo = comm.PhaseFrequencyOffset('FrequencyOffset',freqoffset, ... 'PhaseOffset',phaseoffset,'SampleRate',fs);
Сгенерируйте случайные символы данных, примените 16-QAM модуляцию и передайте модулируемый сигнал через формирующий фильтр импульса передачи.
txMod = qammod(data,M); txSig = txFilter(txMod);
Примените фазу и смещения частоты с помощью pfo Системный объект, и затем передает сигнал через канал AWGN, чтобы добавить белый Гауссов шум.
txSigOffset = pfo(txSig); rxSig = awgnChannel(txSigOffset);
Крупный Системный объект компенсатора частоты обеспечивает грубую коррекцию для смещения частоты. Для условий в этом примере, корректируя смещение частоты полученной коррекции сигнала к в 10 Гц переданного сигнала достаточно.
syncCoarse = coarse(rxSig);
Передайте сигнал через получить импульсный формирующий фильтр и примените прекрасную коррекцию частоты.
rxFiltSig = fine(rxFilter(syncCoarse));
Отобразите схему созвездия первых и последних 1 000 символов в сигнале. Перед сходимостью цикла синхронизации спиральная природа схемы указывает, что смещение частоты не корректируется. После того, как синхронизатор поставщика услуг сходился к решению, символы выравниваются со ссылочным созвездием.
constDiagram([rxFiltSig(1:1000) rxFiltSig(9001:end)])
Демодулируйте сигнал. Объясните задержку сигнала, вызванную передачей, и получите фильтры, чтобы выровнять полученные данные с передаваемыми данными. Вычислите и отобразите общие битовые ошибки и BER. При проверке битовых ошибок используйте более поздний фрагмент полученного сигнала быть уверенными, что цикл синхронизации сходился.
rxData = qamdemod(rxFiltSig,M);
delay = (txFilter.FilterSpanInSymbols + rxFilter.FilterSpanInSymbols) / 2;
idxSync = 2000; % Check BER for the received signal after the synchronization loop has converged
[syncDataTtlErr,syncDataBER] = biterr(data(idxSync:end-delay),rxData(idxSync+delay:end))syncDataTtlErr = 16116
syncDataBER = 0.5042
В зависимости от случайных используемых данных могут быть битовые ошибки, следующие из неоднозначности фазы в полученном сигнале после того, как цикл синхронизации будет сходиться и будет блокировать. В этом случае можно использовать преамбулу, чтобы определить и затем удалить неоднозначность фазы из синхронизируемого сигнала уменьшать битовые ошибки. Если неоднозначность фазы минимальна, количество битовых ошибок может быть неизменным.
idx = 9000 + (1:barker.Length); phOffset = angle(txMod(idx) .* conj(rxFiltSig(idx+delay))); phOffsetEst = mean(phOffset); disp(['Phase offset = ',num2str(rad2deg(phOffsetEst)),' degrees'])
Phase offset = -90.1401 degrees
resPhzSig = exp(1i*phOffsetEst) * rxFiltSig;
Демодулируйте сигнал после решения неоднозначности фазы. Повторно вычислите общие битовые ошибки и BER.
resPhzData = qamdemod(resPhzSig,M); [resPhzTtlErr,resPhzBER] = biterr(data(idxSync:end-delay),resPhzData(idxSync+delay:end))
resPhzTtlErr = 5
resPhzBER = 1.5643e-04
Нарушения канала модели, такие как синхронизация смещения фазы, смещения несущей частоты и фазы поставщика услуг возмещены для сигнала минимального манипулирования сдвига (MSK). Используйте comm.MSKTimingSynchronizer и comm.CarrierSynchronizer Системные объекты, чтобы синхронизировать такие сигналы в получателе. Синхронизатор синхронизации MSK восстанавливает смещение синхронизации, в то время как синхронизатор поставщика услуг восстанавливает смещения фазы и несущая частота.
Инициализируйте системные переменные путем выполнения configureMSKSignalRecoveryEx скрипта MATLAB. Задайте логическую контрольную переменную recoverTimingPhase позволять синхронизировать восстановление фазы и recoverCarrier включить восстановление фазы и несущая частота.
configureMSKSignalRecoveryEx; recoverTimingPhase = true; recoverCarrier = true;
Моделирование нарушений канала
Задайте демонстрационную задержку, timingOffset, то, что модель канала применяется. Создайте переменный дробный объект задержки ввести задержку синхронизации с переданным сигналом.
timingOffset = 0.2; varDelay = dsp.VariableFractionalDelay;
Создайте comm.PhaseFrequencyOffset Системный объект, чтобы ввести фазу поставщика услуг и частоту возмещает к модулируемому сигналу. Поскольку модулятор MSK сверхдискретизировал переданные символы, установите SampleRate свойство к отношению samplesPerSymbol и шаг расчета, Ts.
freqOffset = 50; phaseOffset = 30; pfo = comm.PhaseFrequencyOffset(... 'FrequencyOffset',freqOffset, ... 'PhaseOffset',phaseOffset, ... 'SampleRate',samplesPerSymbol/Ts);
Создайте comm.AWGNChannel Системный объект, чтобы добавить белый Гауссов шум в модулируемый сигнал. Шумовая степень определяется EbNo свойство, которое является энергией, подведенной к долоту к шумовой степени спектральное отношение плотности. Поскольку модулятор MSK генерирует символы с 1 ваттом мощности, установите свойство степени сигнала Системного объекта канала AWGN к 1.
EbNo = 20 + 10*log10(samplesPerSymbol); chAWGN = comm.AWGNChannel(... 'NoiseMethod','Signal to noise ratio (Eb/No)', ... 'EbNo',EbNo,... 'SignalPower',1, ... 'SamplesPerSymbol',samplesPerSymbol);
Синхронизируя фазу, несущую частоту и синхронизацию фазы поставщика услуг
Создайте синхронизатор синхронизации MSK, чтобы восстановить фазу синхронизации символа с помощью метода нелинейности четвертого порядка.
timeSync = comm.MSKTimingSynchronizer(... 'SamplesPerSymbol',samplesPerSymbol, ... 'ErrorUpdateGain',0.02);
Создайте синхронизатор поставщика услуг, чтобы восстановить и несущую частоту и фазу. Поскольку созвездие MSK является QPSK со смещением фазы с 0 степенями, установите comm.CarrierSynchronizer соответственно.
phaseSync = comm.CarrierSynchronizer(... 'Modulation','QPSK', ... 'ModulationPhaseOffset','Custom', ... 'CustomPhaseOffset',0, ... 'SamplesPerSymbol',1);
Потоковый цикл обработки
Симуляция модулирует данные с помощью модуляции MSK. Модулируемые символы проходят через модель канала, которая применяет задержку синхронизации, несущую частоту и сдвиг фазы и аддитивный белый Гауссов шум. Получатель выполняет фазу синхронизации и восстановление фазы и несущую частоту. Наконец, символы сигнала демодулируются, и частота ошибок по битам вычисляется. plotResultsMSKSignalRecoveryEx скрипт генерирует графики рассеивания в этом порядке показать эти эффекты:
Нарушения канала
Синхронизация синхронизации
Синхронизация поставщика услуг
В конце симуляции пример отображает фазу синхронизации, частоту и оценки фазы как функция времени симуляции.
for p = 1:numFrames %------------------------------------------------------------------------ % Generate and modulate data %------------------------------------------------------------------------ txBits = randi([0 1],samplesPerFrame,1); txSym = modem(txBits); %------------------------------------------------------------------------ % Transmit through channel %------------------------------------------------------------------------ % % Add timing offset rxSigTimingOff = varDelay(txSym,timingOffset*samplesPerSymbol); % % Add carrier frequency and phase offset rxSigCFO = pfo(rxSigTimingOff); % % Pass the signal through an AWGN channel rxSig = chAWGN(rxSigCFO); % % Save the transmitted signal for plotting plot_rx = rxSig; % %------------------------------------------------------------------------ % Timing recovery %------------------------------------------------------------------------ if recoverTimingPhase % Recover symbol timing phase using fourth-order nonlinearity % method [rxSym,timEst] = timeSync(rxSig); % Calculate the timing delay estimate for each sample timEst = timEst(1)/samplesPerSymbol; else % Do not apply timing recovery and simply downsample the received % signal rxSym = downsample(rxSig,samplesPerSymbol); timEst = 0; end % Save the timing synchronized received signal for plotting plot_rxTimeSync = rxSym; %------------------------------------------------------------------------ % Carrier frequency and phase recovery %------------------------------------------------------------------------ if recoverCarrier % The following script applies carrier frequency and phase recovery % using a second order phase-locked loop (PLL), and removes phase ambiguity [rxSym,phEst] = phaseSync(rxSym); removePhaseAmbiguityMSKSignalRecoveryEx; freqShiftEst = mean(diff(phEst)/(Ts*2*pi)); phEst = mod(mean(phEst),360); % in degrees else freqShiftEst = 0; phEst = 0; end % Save the phase synchronized received signal for plotting plot_rxPhSync = rxSym; %------------------------------------------------------------------------ % Demodulate the received symbols %------------------------------------------------------------------------ rxBits = demod(rxSym); %------------------------------------------------------------------------ % Calculate the bit error rate %------------------------------------------------------------------------ errorStats = BERCalc(txBits,rxBits); %------------------------------------------------------------------------ % Plot results %------------------------------------------------------------------------ plotResultsMSKSignalRecoveryEx; end
Отобразите частоту ошибок по битам и общее количество символов, обработанных калькулятором коэффициента ошибок.
BitErrorRate = errorStats(1) TotalNumberOfSymbols = errorStats(3)
BitErrorRate =
4.0001e-06
TotalNumberOfSymbols =
499982
Заключение и дальнейшее экспериментирование
Алгоритмы восстановления продемонстрированы при помощи графиков созвездия, взятых после синхронизации, несущей частоты и синхронизации фазы поставщика услуг.
Откройте скрипт, чтобы создать перезаписываемую копию этого примера и его вспомогательных файлов. Затем чтобы показать эффекты алгоритмов восстановления, можно включить и отключить логические контрольные переменные recoverTimingPhase и recoverCarrier и повторно выполненный симуляция.
Приложение
Этот пример использует эти скрипты:
configureMSKSignalRecoveryEx
plotResultsMSKSignalRecoveryEx
removePhaseAmbiguityMSKSignalRecoveryEx
comm.CarrierSynchronizer Системный объект является компенсатором с обратной связью, который использует основанный на PLL алгоритм, описанный в [1]. Выход синхронизатора, y n, является переключенной частотой версией комплексного входного сигнала, x n, для энной выборки. Синхронизатор выход
где λ n является выход прямого цифрового синтезатора (DDS). DDS является версией дискретного времени управляемого напряжением генератора и является базовым компонентом замкнутых циклов фазы дискретного времени. В контексте этого Системного объекта DDS работает фильтром интегрирования.
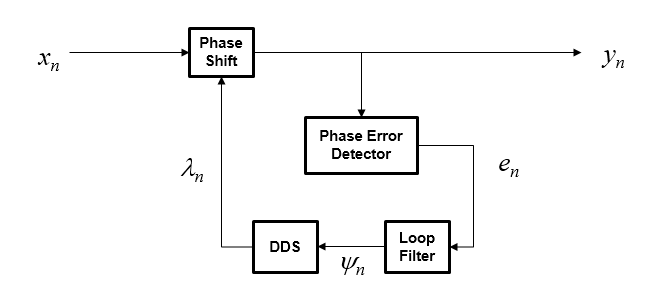
Чтобы откорректировать для смещения частоты, сначала алгоритм определяет ошибку фазы, e n. Значение ошибки фазы зависит от схемы модуляции.
| Модуляция | Ошибка фазы |
|---|---|
| QAM или QPSK |
Для подробного описания этого уравнения см. [1]. |
| BPSK или PAM |
Для подробного описания этого уравнения см. [1]. |
| С 8 PSK | Для подробного описания этого уравнения см. [2]. |
| OQPSK |
|
Чтобы гарантировать устойчивость системы, ошибка фазы проходит через биквадратный контурный фильтр, которым управляют
где ψ n является выход контурного фильтра на выборке n и g, я - усиление интегратора. Усиление интегратора определяется из уравнения
где θ, d, K 0 и K p определяются из свойств Системного объекта. А именно,
где B n является нормированной пропускной способностью цикла, и ζ является фактором затухания. Усиление восстановления фазы, K 0, равно количеству выборок на символ. Тип модуляции определяет усиление детектора ошибок фазы, K p.
| Модуляция | K p |
|---|---|
| BPSK, PAM, QAM, QPSK или OQPSK | 2 |
| С 8 PSK | 1 |
Выход контурного фильтра затем передается DDS. DDS является другим биквадратным контурным фильтром, выражение которого основано на прямом Эйлеровом правиле интегрирования
где g P является пропорциональным усилением, которое выражается как
info объектная функция этого Системного объекта возвращает оценки нормированной полосы захвата, максимальной задержки синхронизации частоты и максимальной задержки синхронизации фазы. Нормированная полоса захвата, (Δf) получение по запросу - в, выражается в радианах и оценивается как
Выражение для (Δf) получения по запросу - в становится менее точным как подходы 1.
Максимальная задержка синхронизации частоты, T FL и задержка синхронизации фазы, T PL, выражается в выборках и оценивается как
[1] Рис, M. Цифровая связь: Подход Дискретного времени. Верхний Сэддл-Ривер, NJ: Prentice Hall, 2009, стр 359–393.
[2] Zhijie, H., И. Чжицян, Цз. Мин и В. Куан. “8PSK Демодуляция для Нового поколения DVB-S2”. 2 004 Международных конференции по вопросам Коммуникаций, Схем и Систем. Издание 2, 2004, стр 1447–1450.
