Компенсируйте модулируемые сигналы с помощью фильтрации обратной связи решения
comm.DecisionFeedbackEqualizer Система object™ использует линию задержки касания фильтра обратной связи решения со взвешенной суммой, чтобы компенсировать модулируемые сигналы, переданные через дисперсионный канал. Объект эквалайзера адаптивно настраивает веса касания на основе выбранного алгоритма. Для получения дополнительной информации см. Алгоритмы.
Компенсировать модулируемые сигналы с помощью фильтра обратной связи решения:
Создайте comm.DecisionFeedbackEqualizer объект и набор его свойства.
Вызовите объект с аргументами, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты? MATLAB.
dfe = comm.DecisionFeedbackEqualizer
dfe = comm.DecisionFeedbackEqualizer(Name,Value)comm.DecisionFeedbackEqualizer('Algorithm','RLS') конфигурирует объект эквалайзера обновить веса касания с помощью алгоритма рекурсивных наименьших квадратов (RLS). Заключите каждое имя свойства в кавычки.
y = dfe(x,tsym,tf)tf. Системный объект запускает обучение когда tf изменения от false к true (в возрастающем ребре). Системный объект обучается до всех символов в tsym обрабатываются. Вход tsym проигнорирован когда tf false. Чтобы включить этот синтаксис, установите свойство Algorithm на 'LMS' или 'RLS' и свойство TrainingFlagInputPort к true.
y = dfe(x,aw)aw весов. Системный объект адаптирует веса касания эквалайзера когда aw true. Если aw false, Системный объект сохраняет веса неизменными. Чтобы включить этот синтаксис, установите свойство Algorithm на 'CMA' и свойство AdaptWeightsSource к 'Input port'.
Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Создайте модулятор BPSK и Систему эквалайзера object™, задав обратную связь решения эквалайзер LMS, имеющий восемь прямых касаний, пять касаний обратной связи и размер шага 0,03.
bpsk = comm.BPSKModulator; eqdfe_lms = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',8,'NumFeedbackTaps',5,'StepSize',0.03);
Измените ссылочный индекс касания эквалайзера.
eqdfe_lms.ReferenceTap = 4;
Создайте набор тестовых данных. Получите данные путем свертки к сигналу.
x = bpsk(randi([0 1],1000,1)); rxsig = conv(x,[1 0.8 0.3]);
Используйте maxstep найти максимальный разрешенный размер шага.
mxStep = maxstep(eqdfe_lms,rxsig)
mxStep = 0.1028
Компенсируйте полученный сигнал. Используйте первые 200 символов в качестве обучающей последовательности.
y = eqdfe_lms(rxsig,x(1:200));
Примените эквализацию обратной связи решения с помощью алгоритма наименьшее количество средних квадратичных (LMS), чтобы восстановиться, символы QPSK прошли через задержанный многопутевой канал AWGN.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
chtaps = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];Сгенерируйте модулируемые QPSK символы. Примените задержанную многопутевую фильтрацию канала и нарушения AWGN к символам.
data = randi([0 M-1], numSymbols, 1);
tx = pskmod(data, M, pi/4);
rx = awgn(filter(chtaps,1,tx),25,'measured');Создайте Системный объект эквалайзера обратной связи решения и отобразите настройку по умолчанию. Настройте ссылочное касание к 1. Проверяйте максимальный разрешенный размер шага. Компенсируйте символы, которым повреждают.
eq = comm.DecisionFeedbackEqualizer
eq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 3
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eq.ReferenceTap = 1; mxStep = maxstep(eq,rx)
mxStep = 0.2141
[y,err,weights] = eq(rx,tx(1:numTrainingSymbols));
Постройте созвездие которым повреждают и компенсируемых символов.
constell = comm.ConstellationDiagram('NumInputPorts',2);
constell(rx,y)
Постройте сигнал ошибки эквалайзера и вычислите величину вектора ошибок компенсируемых символов.
plot(abs(err)) grid on; xlabel('Symbols'); ylabel('|e|')
errevm = comm.EVM; evm = errevm(tx,y)
evm = 10.1621
Постройте веса касания эквалайзера.
subplot(3,1,1); stem(real(weights)); ylabel('real(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1) title('Equalizer Tap Weights') subplot(3,1,2); stem(imag(weights)); ylabel('imag(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1) subplot(3,1,3); stem(abs(weights)); ylabel('abs(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1)
Продемонстрируйте, что эквализация обратной связи решения с помощью алгоритма наименьшее количество средних квадратичных (LMS), чтобы восстановить символы QPSK прошла через канал AWGN. Примените различные планы подготовки эквалайзера и покажите ошибочную величину символа.
Системный Setup
Симулируйте модулируемую QPSK систему, удовлетворяющую AWGN. Передайте пакеты, состоявшие из 200 учебных символов и 1 800 случайных символов данных. Сконфигурируйте обратную связь решения эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; dfeq = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',5,'NumFeedbackTaps',4,'ReferenceTap',3,'StepSize',0.01);
Обучите эквалайзер в начале каждого пакета со сбросом
Процесс каждый пакет с помощью предварительно ожидаемых учебных символов. Сбросьте эквалайзер после обработки каждого пакета. При сбросе эквалайзера после того, как каждый пакет обеспечивает эквалайзер, чтобы обучить касания без априорного знания. Графики сигнала ошибки эквалайзера для первого, второго, и последнего пакета показывают более высокие ошибки символа в начале каждого пакета.
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = dfeq(rx,trainingSymbols); reset(dfeq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end
Обучите эквалайзер в начале каждого пакета без сброса
Процесс каждый пакет с помощью предварительно ожидаемых учебных символов. Не сбрасывайте эквалайзер после того, как каждый пакет будет обработан. Не сбрасывая после каждого пакета, эквалайзер сохраняет веса касания от учебных предшествующих пакетов. Графики сигнала ошибки эквалайзера для первого, второго, и последнего пакета показывают, что после начальной подготовки на первом пакете, последующие пакеты имеют меньше ошибок символа в начале каждого пакета.
release(dfeq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = dfeq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end
Обучайте эквалайзер периодически
Системы с сигналами, удовлетворяющими изменяющимся во времени каналам, требуют, чтобы периодическое обучение эквалайзера обеспечить соединило изменения канала. Задайте систему, которая имеет 200 символов обучения каждым 1 800 символам данных. Между обучением эквалайзер не обновляет веса касания. Процессы эквалайзера 200 символов на пакет.
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);Установите AdaptAfterTraining свойство к false чтобы остановить эквалайзер касаются обновлений веса после учебной фазы.
release(dfeq) dfeq.AdaptAfterTraining = false
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Компенсируйте данные, которым повреждают. Постройте угловую погрешность от канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал варьируется, эквалайзер, выход не удаляет эффекты канала. Кроме того, выходное созвездие вращается из синхронизации, приводящей к битовым ошибкам.
[y,err] = dfeq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')
scatterplot(y)
Установите TrainingInputPort свойство к true сконфигурировать эквалайзер, чтобы переобучить касания, когда сообщено trainFlag входной параметр. Эквалайзер обучается только когда trainFlag true. После каждых 2 000 символов эквалайзер переобучает касания и сохраняет, соединяют изменения канала. Постройте угловую погрешность от канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал варьируется, эквалайзер, выход удаляет эффекты канала. Кроме того, выходное созвездие не вращается из синхронизации, и битовые ошибки уменьшаются.
release(dfeq) dfeq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... dfeq(rx((p-1)*spp+1:p*spp,1),trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')
scatterplot(yVec)
Симулируйте систему с задержкой между переданными символами и полученными выборками. Типичные системы имеют фильтры передатчика и получателя, которые приводят к задержке. Эта задержка должна составляться, чтобы синхронизировать систему. В этом примере системная задержка введена без передачи, и получите фильтры. Эквализация обратной связи решения, с помощью алгоритма наименьшее количество средних квадратичных (LMS), восстанавливает символы QPSK.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;Сгенерируйте модулируемые QPSK символы. Примените многопутевую фильтрацию канала, системную задержку и AWGN к переданным символам.
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
Создайте эквалайзер и Системные объекты EVM. Системный объект эквалайзера задает эквалайзер обратной связи решения с помощью LMS-алгоритма.
dfeq = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',9,'NumFeedbackTaps',6,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
Компенсируйте, не настраивая входную задержку
Компенсируйте полученные символы.
[y1,err1,wts1] = dfeq(rx,tx(1:numTrainingSymbols,1));
Найдите задержку между полученными символами и переданными символами при помощи finddelay функция.
rxDelay = finddelay(tx,rx)
rxDelay = 20
Отобразите информацию об эквалайзере. Значение задержки указывает на задержку, введенную эквалайзером. Вычислите общую задержку как сумму rxDelay и задержка эквалайзера.
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
Пока эквалайзер, выход сходится, коэффициент ошибок символа, не высок. Постройте вывод ошибок, err1, определить, когда компенсируемый выход сходится.
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')
График показывает чрезмерные ошибки для первых 2 000 символов. При демодуляции символов и вычислительных ошибок символа, объясните не сходившийся выход и системную задержку между эквалайзером выход и переданными символами.
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 6001
evmWithDelay = evm(y1)
evmWithDelay = 25.6868
Коэффициент ошибок и EVM высоки, потому что получить задержка не составлялась в Системном объекте эквалайзера.
Настройте входную задержку эквалайзера обратной связи решения
Компенсируйте полученные данные при помощи значения задержки, чтобы установить InputDelay свойство. Начиная с InputDelay ненастраиваемое свойство, необходимо выпустить dfeq Системный объект, чтобы реконфигурировать InputDelay свойство. Компенсируйте полученные символы.
release(dfeq) dfeq.InputDelay = rxDelay
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 9
NumFeedbackTaps: 6
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = dfeq(rx,tx(1:numTrainingSymbols,1));
Постройте веса касания и компенсируемую ошибочную величину. Диаграмма стебель-листья показывает, что веса касания эквалайзера до и после системной задержки удалены. 2D график показывает более медленную сходимость эквалайзера для задержанного сигнала, по сравнению с сигналом с удаленной задержкой.
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on
figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on
Постройте вывод ошибок компенсируемых сигналов, rxDelayed и rxDelayRemoved. Для сигнала, которому удалили задержку, эквалайзер сходится во время 1 000 периодов подготовки символа. Когда демодуляция символов и вычислительных ошибок символа, чтобы составлять не сходившийся выход и системную задержку между эквалайзером выход и переданными символами, пропускает первые 500 символов. Реконфигурирование эквалайзера, чтобы составлять системную задержку включает лучшую эквализацию сигнала и уменьшает ошибки символа и EVM.
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 7.5147
Восстановите символы QPSK с эквалайзером решения, с помощью постоянного алгоритма модуля (CMA) и основанного на EVM обучения касаний. При использовании слепых алгоритмов эквалайзера, таких как CMA, можно обучить касания эквалайзера с помощью AdaptWeights свойство запуститься и остановить обучение. Используйте функции помощника, чтобы сгенерировать графики и применить коррекцию фазы.
Инициализируйте системные переменные.
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; refTap = 3; nFwdTaps = 5; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -12],'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
Создайте эквалайзер и Системные объекты EVM. Системный объект эквалайзера задает эквалайзер обратной связи решения с помощью CMA адаптивный алгоритм. Вызовите функцию помощника, чтобы инициализировать графики фигуры.
dfeq = comm.DecisionFeedbackEqualizer('Algorithm','CMA', ... 'NumForwardTaps',nFwdTaps,'NumFeedbackTaps',nFdbkTaps,'ReferenceTap',refTap, ... 'StepSize',0.03,'AdaptWeightsSource','Input port')
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'CMA'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0300
Constellation: [1x4 double]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(dfeq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = initFigures(numPackets,ttlTaps);
Цикл эквализации
Выполните эти шаги, чтобы реализовать цикл эквализации.
Сгенерируйте пакеты данных OQPSK.
Примените Релеевское замирание и AWGN к данным о передаче.
Примените эквализацию к полученным данным и коррекцию фазы к эквалайзеру выход.
Оцените EVM и переключите adaptWeights отметьте к true или false на основе уровня EVM.
Обновите графики фигуры.
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = dfeq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end
rxDelay
rxDelay = 0
Графики фигуры показывают, что, когда EVM варьируется, переключатели эквалайзера в и из направленного на решение режима адаптации веса.
Функции помощника
Эта функция помощника инициализирует фигуры, которые показывают квадратический график результатов симуляции.
function [errPlot,evmPlot,scatter,adaptState] = initFigures(numPkts,ttlTaps) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(ttlTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 ttlTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
Эта функция помощника обновляет фигуры.
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
Эта функция помощника применяет коррекцию фазы.
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
Восстановите символы QPSK в исчезающих средах с эквалайзером обратной связи решения, с помощью алгоритма наименьшее количество средних квадратичных (LMS). Используйте reset возразите функции, чтобы компенсировать независимые пакеты. Используйте функции помощника, чтобы сгенерировать графики. Этот пример также показывает основанную на символе обработку и основанную на системе координат обработку.
Настройка
Инициализируйте системные переменные, создайте Системный объект эквалайзера и инициализируйте фигуры графика.
M = 4; % QPSK numSym = 1000; numTrainingSym = 100; numPackets = 5; refTap = 5; nFwdTaps = 9; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; stepsz = 0.01; ttlNumSym = numSym + numTrainingSym; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -9], ... 'MaximumDopplerShift',0, ... 'PathGainsOutputPort',true); SNR = 35; rxVec = zeros(ttlNumSym,numPackets); txVec = zeros(ttlNumSym,numPackets); yVec = zeros(ttlNumSym,1); eVec = zeros(ttlNumSym,1); dfeq1 = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps,'NumFeedbackTaps',nFdbkTaps,'ReferenceTap',refTap, ... 'StepSize',stepsz,'TrainingFlagInputPort',true); [errPlot,wStem,hStem,scatPlot] = initFigures(ttlNumSym,ttlTaps, ... raylChan.AveragePathGains);
Основанная на символе обработка
Для основанной на символе обработки обеспечьте один символ во входе эквалайзера. Сбросьте состояние эквалайзера и канал после обработки каждого пакета.
for p = 1:numPackets trainingFlag = true; for q=1:ttlNumSym data = randi([0 M-1],1,1); tx = pskmod(data,M,pi/4); [xc,pg] = raylChan(tx); rx = awgn(xc,25); [y,err,wts] = dfeq1(rx,tx,trainingFlag);
Отключите обучение после обработки numTrainingSym учебные символы.
if q == numTrainingSym trainingFlag = false; end updateFigures(errPlot,wStem,hStem,scatPlot,err,wts,y,pg,q,ttlNumSym); txVec(q,p) = tx; rxVec(q,p) = rx; end
После обработки каждого пакета сброс Системный объект канала, чтобы получить новую реализацию канала касается и Системный объект эквалайзера, чтобы восстановить веса касаний по умолчанию.
reset(raylChan)
reset(dfeq1)
end
Основанная на пакете обработка
Для основанной на пакете обработки обеспечьте один пакет во входе эквалайзера. Каждый пакет содержит ttlNumSym символы. Поскольку учебная длительность меньше пакетной длины, вы не должны задавать вход начинать-обучения.
yVecPkt = zeros(ttlNumSym,numPackets); errVecPkt = zeros(ttlNumSym,numPackets); wgtVecPkt = zeros(ttlTaps,numPackets); dfeq2 = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps,'NumFeedbackTaps',nFdbkTaps,'ReferenceTap',refTap, ... 'StepSize',stepsz); for p = 1:numPackets [yVecPkt(:,p),errVecPkt(:,p),wgtVecPkt(:,p)] = ... dfeq2(rxVec(:,p),txVec(1:numTrainingSym,p)); for q=1:ttlNumSym updateFigures(errPlot,wStem,hStem,scatPlot, ... errVecPkt(q,p),wgtVecPkt(:,p),yVecPkt(q,p),pg,q,ttlNumSym); end
После обработки каждого пакета сброс Системный объект канала, чтобы получить новую реализацию канала касается и Системный объект эквалайзера, чтобы восстановить веса касаний по умолчанию.
reset(raylChan)
reset(dfeq2)
end
Функции помощника
Эта функция помощника инициализирует фигуры.
function [errPlot,wStem,hStem,scatPlot] = initFigures(ttlNumSym,ttlTap,pg) yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); wVec = zeros(ttlTap,1); figure; subplot(2,2,1); wStem = stem(wVec); axis([1 ttlTap 0 1.8]); grid on xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2); hStem = stem([0 abs(pg) 0]); grid on; xlabel('Taps'); ylabel('|Path Gain|'); title('Channel Path Gain Magnitude') subplot(2,2,3); errPlot = plot(eVec); axis([1 ttlNumSym 0 1.2]); grid on xlabel('Symbols'); ylabel('|Error Magnitude|'); title('Error Magnitude') subplot(2,2,4); scatPlot = plot(yVec,'.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title(sprintf('Scatter Plot')); end
Эта функция помощника обновляет фигуры.
function updateFigures(errPlot,wStem,hStem,scatPlot, ... err,wts,y,pg,p,ttlNumSym) persistent yVec eVec if p == 1 yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); end yVec(p) = y; eVec(p) = abs(err); errPlot.YData = abs(eVec); wStem.YData = abs(wts); hStem.YData = [0 abs(pg) 0]; scatPlot.XData = real(yVec); scatPlot.YData = imag(yVec); drawnow limitrate end
Эквалайзер обратной связи решения (DFE) является нелинейным эквалайзером, который уменьшает интерференцию межсимвола (ISI) в выборочных частотой каналах. Если пустой указатель существует в частотной характеристике канала, DFEs не улучшают шум. DFE состоит из коснувшейся линии задержки, которая хранит выборки от входного сигнала и содержит прямой фильтр и фильтр обратной связи. Прямой фильтр похож на линейный эквалайзер. Фильтр обратной связи содержит коснувшуюся линию задержки, входные параметры которой являются решениями, принятыми о компенсируемом сигнале. Однажды на период символа, эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
DFEs может быть расположен с интервалами символом или дробный расположенный с интервалами символом.
Для расположенного с интервалами символом эквалайзера количество выборок на символ, K, равняется 1. Выходная частота дискретизации равняется входной частоте дискретизации.
Для дробного расположенного с интервалами символом эквалайзера количество выборок на символ, K, является целым числом, больше, чем 1. Как правило, K 4 для дробных расположенных с интервалами символом эквалайзеров. Выходная частота дискретизации является 1/T, и входной частотой дискретизации является K/T. Коснитесь обновление веса происходит при норме выработки.
Это схематические показы дробный расположенный с интервалами символом DFE в общей сложности с весами N, периодом символа T и выборками K на символ. Фильтр имеет L прямые веса и N-L веса обратной связи. Прямой фильтр наверху, и фильтр обратной связи в нижней части. Если K равняется 1, результатом является расположенный с интервалами символом DFE вместо дробного расположенного с интервалами символом DFE.
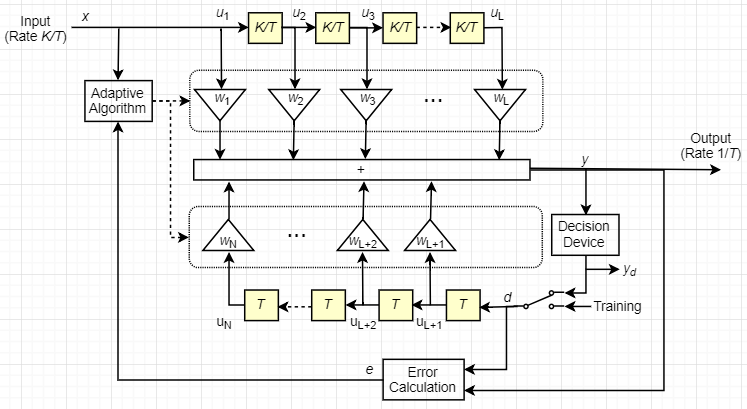
В каждый период символа эквалайзер получает выборки входа K в прямом фильтре и одно решение или учебную выборку в фильтре обратной связи. Эквалайзер затем выводит взвешенную сумму значений в форварде и линиях задержки обратной связи и обновляет веса, чтобы подготовиться к следующему периоду символа.
Алгоритм для блока Adaptive Algorithm в схематическом совместно оптимизирует веса обратной связи и форвард. Объединенная оптимизация особенно важна для сходимости в алгоритме рекурсивного наименьшего квадрата (RLS).
Для получения дополнительной информации смотрите Эквализацию.