Cоединение обратной связи многих моделей
sys = feedback(sys1,sys2)sys для соединения отрицательной обратной связи объектов модели sys1,sys2.
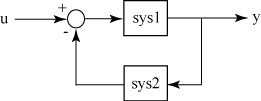
От фигуры, модели sys с обратной связью имеет u как входной вектор и y как выходной вектор. Обе модели, sys1 и sys2, должно или быть непрерывным или дискретным с идентичными шагами расчета.
sys = feedback(___,sign)sys для обратной связи с типом обратной связи, заданной sign. По умолчанию, feedback принимает отрицательную обратную связь и эквивалентен feedback(sys1,sys2,-1). Чтобы вычислить систему с обратной связью с положительной обратной связью, используйте sign = +1.
Связь обратной связи должна быть свободна от алгебраических циклов. Например, если D1 и D2 являются проходными матрицами sys1 и sys2, это условие эквивалентно:
I + D1D2, несингулярный при использовании отрицательной обратной связи
I − D1D2, несингулярный при использовании положительной обратной связи