Синтаксис

Описание

rlqg = lqgreg(kest,k) возвращает регулятор LQG rlqg (модель в пространстве состояний), учитывая Оценку состояния фильтра Калмана kest и обратная связь состояния получает матричный k. Те же указатели на функцию, и непрерывные - и случаи дискретного времени. Используйте сопоставимые инструменты, чтобы спроектировать kest и k:

В дискретное время, lqgreg производит регулятор

Для получения дополнительной информации об Оценках состояния фильтра Калмана смотрите kalman страница с описанием.

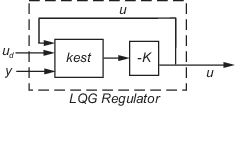
rlqg = lqgreg(kest,k,controls) средства оценки указателей, которые имеют доступ к дополнительному детерминированному известному объекту, вводят _ud. Вектор индекса controls затем задает, какие входные параметры средства оценки являются средствами управления u и получившийся регулятор LQG rlqg имеет _ud и y как входные параметры (см. следующую фигуру).

Алгоритмы

lqgreg формирует регулятор "линейного квадратичного гауссова" (LQG) путем соединения Оценки состояния фильтра Калмана, спроектированной с kalman и оптимальное усиление обратной связи состояния спроектировано с lqr, dlqr, или lqry. Регулятор LQG минимизирует некоторую квадратичную функцию стоимости, которая обменивает производительность регулирования и усилие по управлению. Этот регулятор является динамическим и использует шумные выходные измерения, чтобы сгенерировать команды регулирования.

В непрерывное время регулятор LQG генерирует команды

где $$\widehat{x}$$ оценка состояния Кальмана. Уравнения пространства состояний регулятора

где y является вектором объекта выходные измерения (см. kalman для фона и обозначения). Следующая схема показывает этому динамическому регулятору относительно объекта.

В дискретное время можно сформировать регулятор LQG, использующий любого задержанная оценка состояния $$\widehat{x}[n|n-1]$$ из x [n], на основе измерений до y [n–1] или оценка текущего состояния $$\widehat{x}[n|n]$$, на основе всех доступных измерений включая y [n]. В то время как регулятор

всегда четко определено, текущий регулятор

является причинным только, когда I-KMD является обратимым (см. kalman для обозначения). Кроме того, практические реализации текущего регулятора должны позволить в течение времени вычислений, требуемого вычислить u [n] после измерений, y [n] становится доступным (это составляет задержку обратной связи).

Для объекта дискретного времени уравнениями:

соединение "текущей" Оценки состояния фильтра Калмана к усилению LQR оптимально только когда $$E\left(w\left[n\right]v{\left[n\right]}^{\prime }\right)=0$$ и y [n] не зависит от w [n] (H = 0). Если этим условиям не удовлетворяют, вычисляют оптимальный контроллер LQG, использующий lqg.

Смотрите также

dlqr | kalman | kalmd | lqr | lqrd | lqry | reg