lqgtrack

Сформируйте контроллер сервомотора "линейного квадратичного гауссова" (LQG)

Синтаксис

C = lqgtrack(kest,k) C = lqgtrack(kest,k,'2dof') C = lqgtrack(kest,k,'1dof') C = lqgtrack(kest,k,...CONTROLS)

Описание

lqgtrack формирует контроллер сервомотора "линейного квадратичного гауссова" (LQG) с интегральным действием для цикла, показанного в следующем рисунке. Этот компенсатор гарантирует, что выход y отслеживает ссылочную команду r и отклоняет воздействия процесса w и шум измерения v. lqgtrack принимает, что r и y имеют ту же длину.

Примечание

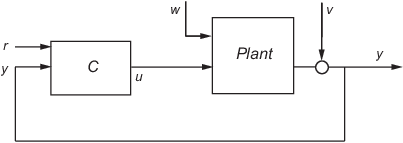
Всегда используйте положительную обратную связь, чтобы подключить контроллер сервомотора LQG C к объекту выход y.

C = lqgtrack(kest,k) формирует две степени свободы контроллер сервомотора LQG C путем соединения Оценки состояния фильтра Калмана kest и обратная связь состояния получает k, как показано в следующем рисунке. C имеет входные параметры $[r; y]$ и генерирует команду $u = - K [\hat{x}; x_{i}]$ , где $\hat{x}$ оценка Кальмана состояния объекта, и _xi является интегратором выход.

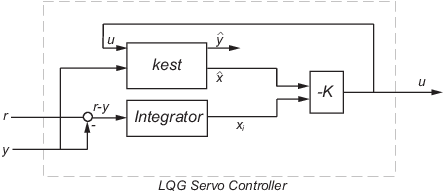
Размер матрицы усиления k определяет длину _xi. _xi, y и r у всех есть та же длина.

Две степени свободы контроллер сервомотора LQG уравнения пространства состояний

$\begin{array}{l} [\begin{matrix} \dot{\hat{x}} \\ {\dot{x}}_{i} \end{matrix}] = [\begin{matrix} A - B K_{x} - L C + L D K_{x} & - B K_{i} + L D K_{i} \\ 00 \end{matrix}] [\begin{matrix} \hat{x} \\ x_{i} \end{matrix}] + [\begin{matrix} 0 & L \\ I & - I \end{matrix}] [\begin{matrix} r \\ y \end{matrix}] \\ u = [\begin{matrix} - K_{x} & - K_{i} \end{matrix}] [\begin{matrix} \hat{x} \\ x_{i} \end{matrix}] \end{array}$

Примечание

Синтаксис C = lqgtrack(kest,k,'2dof') эквивалентно C = lqgtrack(kest,k).

C = lqgtrack(kest,k,'1dof') формирует одну степень свободы контроллер сервомотора LQG C это берет ошибку отслеживания e = r – y, как введено вместо [r; y], как показано в следующем рисунке.

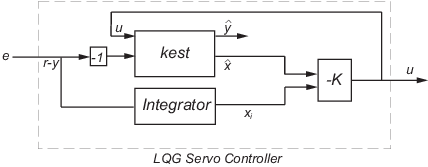
Одна степень свободы контроллер сервомотора LQG уравнения пространства состояний

$\begin{array}{l} [\begin{matrix} \dot{\hat{x}} \\ {\dot{x}}_{i} \end{matrix}] = [\begin{matrix} A - B K_{x} - L C + L D K_{x} & - B K_{i} + L D K_{i} \\ 00 \end{matrix}] [\begin{matrix} \hat{x} \\ x_{i} \end{matrix}] + [\begin{matrix} - L \\ I \end{matrix}] e \\ u = [\begin{matrix} - K_{x} & - K_{i} \end{matrix}] [\begin{matrix} \hat{x} \\ x_{i} \end{matrix}] \end{array}$

C = lqgtrack(kest,k,...CONTROLS) формирует контроллер сервомотора LQG C когда Оценка состояния фильтра Калмана kest имеет доступ к дополнительным известным (детерминированным) командам _Ud объекта. В векторе индекса CONTROLS, задайте который входные параметры kest каналы управления u. Получившийся компенсатор C имеет входные параметры

[_Ud; r; y] в двух случаях степени свободы
[_Ud; e] в одном случае степени свободы

Соответствующая структура компенсатора для двух случаев степени свободы появляется в следующем рисунке.

Примеры

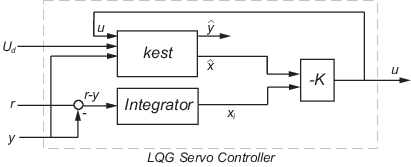
См. Проект в качестве примера Контроллер Сервомотора LQG.

Советы

Можно использовать lqgtrack и для непрерывного - и для системы дискретного времени.

В системах дискретного времени интеграторы основаны на прямом Эйлере (см. lqi для деталей). Оценка состояния $\hat{x}$ любой x [n |n] или x [n |n–1], в зависимости от типа средства оценки (см. kalman для деталей).

Для объекта дискретного времени уравнениями:

$\begin{matrix} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] {Измерения} \end{matrix}$

соединение "текущей" Оценки состояния фильтра Калмана к усилению LQR оптимально только когда $E (w [n] v {[n]}^{'}) = 0$ и y [n] не зависит от w [n] (H = 0). Если этим условиям не удовлетворяют, вычисляют оптимальный контроллер LQG, использующий lqg.

Документация

lqgtrack

Синтаксис

Описание

Примечание

Примечание

Примеры

Советы

Смотрите также

Представленный в R2008b

Документация Control System Toolbox

Поддержка