Документация

Анализ систем с задержками

Можно использовать аналитические команды, такие как step, bode, или margin анализировать системы с задержками. Программное обеспечение не делает приближений при выполнении такого анализа.

Например, рассмотрите следующий цикл управления, где объект моделируется как первый порядок плюс потеря времени:

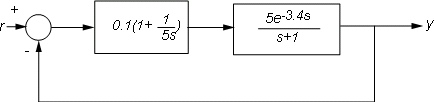
Можно смоделировать систему с обратной связью от r к y со следующими командами:

s = tf('s');
P = 5*exp(-3.4*s)/(s+1);
C = 0.1 * (1 + 1/(5*s));
T = feedback(P*C,1);

T модель в пространстве состояний с внутренней задержкой. Для получения дополнительной информации о моделях с внутренними задержками, смотрите закрывающуюся Обратную связь с Задержками.

Постройте переходной процесс T:

stepplot(T)

Для более сложных соединений можно назвать сигналы ввода и вывода каждого блока и использовать connect автоматически заботиться о проводном соединении. Предположим, например, что вы хотите добавить feedforward в цикл управления предыдущей модели.

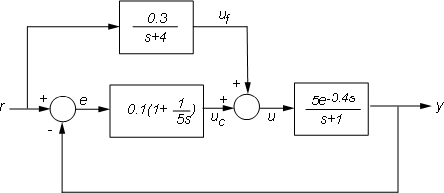
Можно вывести соответствующую модель Tff с обратной связью

F = 0.3/(s+4);
P.InputName = 'u';  
P.OutputName = 'y';
C.InputName = 'e';  
C.OutputName = 'uc';
F.InputName = 'r';  
F.OutputName = 'uf';
Sum1 = sumblk('e','r','y','+-');    % e = r-y
Sum2 = sumblk('u','uf','uc','++');  % u = uf+uc
Tff = connect(P,C,F,Sum1,Sum2,'r','y');

и сравните, его ответ с обратной связью только проектируют.

stepplot(T,Tff)
legend('No feedforward','Feedforward')

Представление пространства состояний отслеживает внутренние задержки обеих моделей.

s = tf('s');
G = exp(-5*s)/(s+1);
T = feedback(G,.5);
bodemag(T)

G = 1 + 0.5 * exp(-3*s);
bodemag(G)

G = exp(-s) * (0.8*s^2+s+2)/(s^2+s);
T = feedback(G,1);
stepplot(T)

G = 1/(s+1) + exp(-4*s);
T = feedback(1,G);
stepplot(T,150)

Связанные примеры

• Закрытие обратной связи с задержками

Больше о

• Задержки линейных систем
• Внутренние задержки