Линейные варьирующиеся по параметру модели

Что такое Линейные Варьирующиеся по параметру Модели?

linear parameter-varying (LPV), система является линейной моделью в пространстве состояний, движущие силы которой варьируются как функция определенных изменяющихся во времени параметров под названием scheduling parameters. В MATLAB^® модель LPV представлена в форме пространства состояний с помощью коэффициентов, которые являются зависимым параметра.

Математически, система LPV представлена как:

\begin{array}{l} d x (t) = A (p) x (t) + B (p) u (t) \\ y (t) = C (p) x (t) + D (p) u (t) \\ x (0) = x_{0} \end{array}

(1)

где

u(t) входные параметры
y(t) выходные параметры
x(t) состояния модели с начальным значением x0
$d x (t)$ производный вектор состояния $\dot{x}$ для систем непрерывного времени и вектора обновления состояния $x (t + Δ T)$ для систем дискретного времени. ΔT является шагом расчета.
A(p), B(p), C(p) и D(p) матрицы пространства состояний, параметризованные вектором параметра планирования p.
Параметры p = p(t) измеримые функции входных параметров и состояния модели. Они могут быть скаляром или вектором нескольких параметров. Набор планирования параметров задает пробел планирования, по которому задана модель LPV.

Основанная на сетке модель LPV

Распространенный способ представлять модели LPV как интерполированный массив линейных моделей в пространстве состояний. Определенное число точек на пробеле планирования выбрано, обычно формируя обычную сетку. Система LTI присвоена каждой точке, представляя динамику в локальной близости той точки. Динамика при планировании местоположений, промежуточных узлы решетки, получена интерполяцией систем LTI в соседних точках.

Например, аэродинамическое поведение самолета часто планируется по сетке угла установки (α) и скорость ветра (V) значения. Для каждого параметра планирования область значений значений выбрана, такие как α = 0:5:20 степени, V = 700:100:1400 м/с. Для каждой комбинации (α, V) значения, получена линейная аппроксимация поведения самолета. Локальные модели соединяются как показано в следующем рисунке:

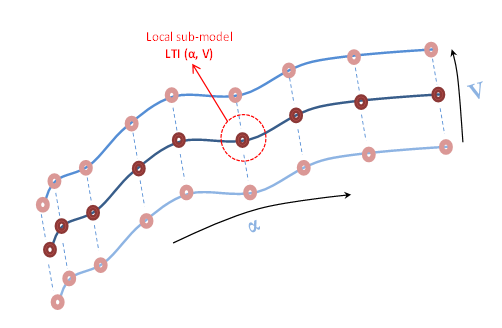
Каждый пончик представляет локальную модель LTI, и соединяющиеся кривые представляют правила интерполяции. Абсцисса и ордината поверхности являются параметрами планирования (α, V).

Эта форма иногда называется основанным на сетке представлением LPV. Это - форма, используемая блоком LPV System. Для значимых интерполяций системных матриц все локальные модели должны использовать то же основание состояния.

Аффинная форма модели LPV

Системное представление LPV может быть расширено, чтобы позволить смещения в dxXU и y переменные. Эта форма известна как affine form модели LPV. Математически, следующее представляет систему LPV:

\begin{array}{l} d x (t) = A (p) x (t) + B (p) u (t) + (\bar{d x} (p) - A (p) \bar{x} (p) - B (p) \bar{u} (p)) \\ y (t) = C (p) x (t) + D (p) u (t) + (\bar{y} (p) - C (p) \bar{x} (p) - D (p) \bar{u} (p)) \\ x (0) = x_{0} \end{array}

(2)

$\bar{d x} (p), \bar{x} (p), \bar{u} (p), \bar{y} (p)$ смещения в значениях dx(t)xt , u(t) и y(t) в данном значении параметров p = p(t).

Чтобы получить такие представления массива линейной системы, линеаризуйте модель Simulink^® по пакету рабочих точек (см. Пакетную Линеаризацию (Simulink Control Design).) Смещения соответствуют рабочим точкам, в которых вы линеаризовали модель.

Можно получить смещения путем возврата дополнительной информации о линеаризации при вызывании функций, таких как linearize или getIOTransfer. Можно затем извлечь смещения с помощью getOffsetsForLPV. Для примера см. Приближение LPV Модели Конвертера Повышения (Simulink Control Design).

В аффинном представлении, линейной модели в данной точке p = p* в планировании пробел:

$\begin{array}{l} d Δ x (t, p^{*}) = A (p^{*}) Δ x (t, p^{*}) + B (p^{*}) Δ u (t, p^{*}) \\ Δ y (t, p^{*}) = C (p^{*}) Δ x (t, p^{*}) + D (p^{*}) Δ u (t, p^{*}) \end{array}$

Состояния этой линейной модели связаны с состояниями полной модели LPV (уравнение 2) $Δ x (t, p^{*}) = x (t) - \bar{x} (p^{*})$ . Точно так же $Δ y (t, p^{*}) = y (t) - \bar{y} (p^{*})$ и $Δ u (t, p^{*}) = u (t) - \bar{u} (p^{*})$ .

Регулярный по сравнению с неправильными сетками

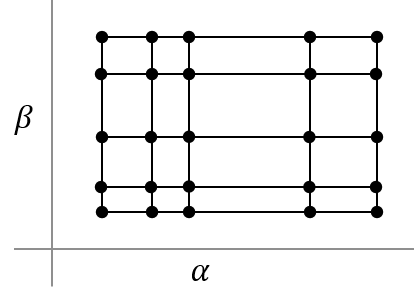
Рассмотрите систему, которая использует два параметра планирования, α и β. Когда α и β варьируются монотонно, обычная сетка формируется, как показано в следующей фигуре. Массив пространства состояний содержит значение в каждой комбинации значения β и α. Обычная сетка не подразумевает универсальный интервал между значениями.

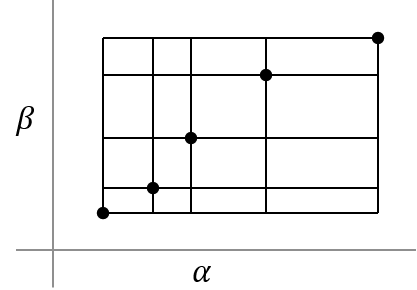
Когда параметры co-vary, то есть, α и β увеличиваются вместе, неправильная сетка формируется. Системные параметры массива доступны только по диагонали в плоскости параметра.

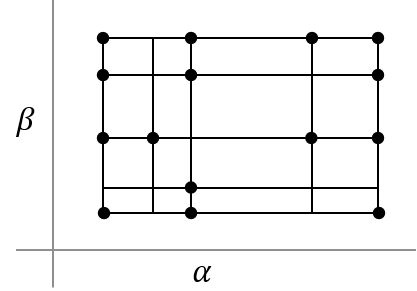
Если определенные выборки отсутствуют в в противном случае обычной сетке, сетка считается неправильной.

Используйте массивы моделей, чтобы создать линейные варьирующиеся по параметру модели

Массив линейных моделей состояния сопоставимых, которые задают модель LPV, представлен массивом объектов модели в пространстве состояний. Для получения дополнительной информации о массивах моделей смотрите Массивы моделей.

Системный размер массивов равен размеру сетки в планировании пробела. В примере самолета принимает α, 5 значений в области значений степеней 0–20 и V принимают 8 значений в области значений на 700-1400 м/с. Если вы задаете линейную модель в каждой комбинации (α, V) значения (т.е. сетка обычна), размер сетки 5 8. Поэтому размер массива моделей должен быть 5 8.

Информация о планировании параметров присоединена к линейному массиву моделей с помощью своего SamplingGrid свойство. Значение SamplingGrid свойство должно быть структурой со столькими же полей, сколько там планируют параметры. Для каждого поля значение должно быть установлено ко всем значениям, принятым соответствующей переменной на пробеле планирования.

Для примера самолета можно задать SamplingGrid свойство как:

Alpha = 0:5:20; 
V = 700:100:1400;
[Alpha_Grid,V_Grid] = ndgrid(Alpha, V);
linsysArray.SamplingGrid = struct('Alpha',Alpha_Grid,'V',V_Grid);

Аппроксимируйте Нелинейные Системы с помощью Моделей LPV

Таким же образом, когда линейная модель обеспечивает приближение поведения системы в данных условиях работы, модель LPV обеспечивает приближение поведения по промежутку на условиях работы. Общий подход для построения модели LPV пакетной обрезкой и линеаризацией, сопровождаемой путем укладки локальных моделей в массиве модели в пространстве состояний.

Примечание

При получении линейных моделей линеаризацией не уменьшайте или изменяйте переменные состояния, используемые моделями.

Операционная область обычно имеет высокую размерность, потому что она состоит из всех входных переменных и переменных состояния. Генерация или интерполяция локальных моделей в таких высоких мерных пространствах обычно неосуществимы. Более простой подход должен использовать маленький набор планирования параметров как прокси для операционных пространственных переменных. Параметры планирования выведены из входных параметров и переменных состояния исходной системы. Необходимо выбрать значения тщательно так, чтобы для фиксированного значения параметров планирования, поведение системы было приблизительно линейно. Этот подход не всегда возможен.

Считайте нелинейную систему описанной следующими уравнениями:

$\begin{array}{l} {\dot{x}}_{1} = x_{}^{12} + x_{}^{22} \\ {\dot{x}}_{2} = - 2 x_{1} - 3 x_{2} + 2 u \\ y = x_{1} + 2 \end{array}$

Предположим, что вы используете $p (t) = {\dot{x}}_{1}$ как переменная планирования. В установленный срок мгновенный t = t ₀, вы имеете:

$\begin{array}{l} {\dot{x}}_{1} \approx 2 x_{1} (t_{0}) x_{1} + 2 x_{2} (t_{0}) x_{2} - {\dot{x}}_{1} (t_{0}) \\ {\dot{x}}_{2} = - 2 x_{1} - 3 x_{2} + 2 u \\ y = x_{1} + 2 \end{array}$

Таким образом движущие силы линейны (аффинно) в окружении данного значения $\dot{x}$ . Приближение содержит навсегда промежутки и значения входа u как долго с $\dot{x}$ не отклоняет очень от его номинальной стоимости при выборке точки t ₀. Обратите внимание на то, что планируя на вход u или состояния x ₁ или x ₂ не помогает локально линеаризовать систему. Поэтому они не хорошие кандидаты на планирование параметров.

Для примера этого подхода смотрите, что Аппроксимирующее Нелинейное Поведение Использует Массив Систем LTI (Simulink Control Design).

Приложения линейных варьирующихся по параметру моделей

Моделирование многорежимной динамики

Можно использовать модели LPV, чтобы представлять системы, которые показывают несколько режимов (режимы) операции. Примеры таких систем включают сталкивающиеся тела, системы, которыми управляют переключатели оператора и приближения систем, воздействовавших сухим трением и гистерезисными эффектами. Для примера смотрите Используя Массивы LTI для Симуляции Многорежимной Динамики.

Моделирование прокси для более быстрых симуляций

Этот подход полезен для генерации суррогатных моделей, которые можно использовать вместо исходной системы во включении более быстрых симуляций, уменьшая объем потребляемой памяти кода целевого компьютера и симуляции оборудования в цикле (HIL). Можно также использовать суррогатные модели этого типа для разработки запланированных на усиление контроллеров и для инициализации задач оценки параметра в Simulink. Для примера аппроксимации общего нелинейного поведения системы моделью LPV смотрите, что Аппроксимирующее Нелинейное Поведение Использует Массив Систем LTI (Simulink Control Design).

Модели LPV могут помочь ускорить симуляцию физических компонентно-ориентированных систем, таких как те созданное программное обеспечение Simscape™ Multibody™ и Simscape Electrical™ Power Systems использования. Для примера этого подхода см. Приближение LPV Модели Конвертера Повышения (Simulink Control Design).

Смотрите также

LPV System | getOffsetsForLPV

Документация