Динамические нейронные сети способны к прогнозу timeseries. Чтобы видеть примеры использования сетей NARX, применяемых в форме разомкнутого цикла, форме с обратной связью и открытом / замкнутом цикле многоступенчатый прогноз, см. Многоступенчатый Прогноз Нейронной сети.
Для глубокого обучения для данных временных рядов смотрите вместо этого Классификацию Последовательностей Используя Глубокое обучение.
Предположим, например, что у вас есть данные из процесса нейтрализации pH. Вы хотите спроектировать сеть, которая может предсказать pH решения в баке от прошлых значений pH и прошлых значений кислотной и основной скорости потока жидкости в бак. У вас есть в общей сложности 2 001 временной шаг, для которых у вас есть те ряды.
Можно решить эту задачу двумя способами:
Используйте графический интерфейс пользователя, ntstool, как описано в Использовании Приложения Временных рядов Нейронной сети.
Используйте функции командной строки, как описано в Использовании Функций Командной строки.
Обычно лучше запуститься с графический интерфейса пользователя, и затем использовать графический интерфейс пользователя, чтобы автоматически сгенерировать скрипты командной строки. Перед использованием любого метода первый шаг должен описать задачу путем выбора набора данных. Каждый графический интерфейс пользователя имеет доступ ко многим наборам выборочных данных, которые можно использовать, чтобы экспериментировать с тулбоксом. Если у вас есть определенная задача, которую вы хотите решить, можно загрузить собственные данные в рабочую область. Следующий раздел описывает формат данных.
Чтобы описать задачу временных рядов для тулбокса, расположите набор входных векторов TS как столбцы в массиве ячеек. Затем расположите другой набор целевых векторов TS (правильные выходные векторы для каждого из входных векторов) во второй массив ячеек (см. “Структуры данных” для подробного описания форматирования данных для статического и данных временных рядов). Однако существуют случаи, в которых у вас только должен быть целевой набор данных. Например, можно описать следующую задачу временных рядов, в которой вы хотите использовать предыдущие значения ряда, чтобы предсказать следующее значение:
targets = {1 2 3 4 5};
Следующий раздел показывает, как обучить сеть, чтобы соответствовать набору данных временных рядов, с помощью приложения временных рядов нейронной сети, ntstool. Этот пример использует набор данных нейтрализации pH, которому предоставляют тулбокс.
В случае необходимости откройтесь, Нейронная сеть Запускают графический интерфейс пользователя с этой команды:
nnstart
Нажмите Time Series App, чтобы открыть Приложение Временных рядов Нейронной сети. (Можно также использовать команду ntstool.)
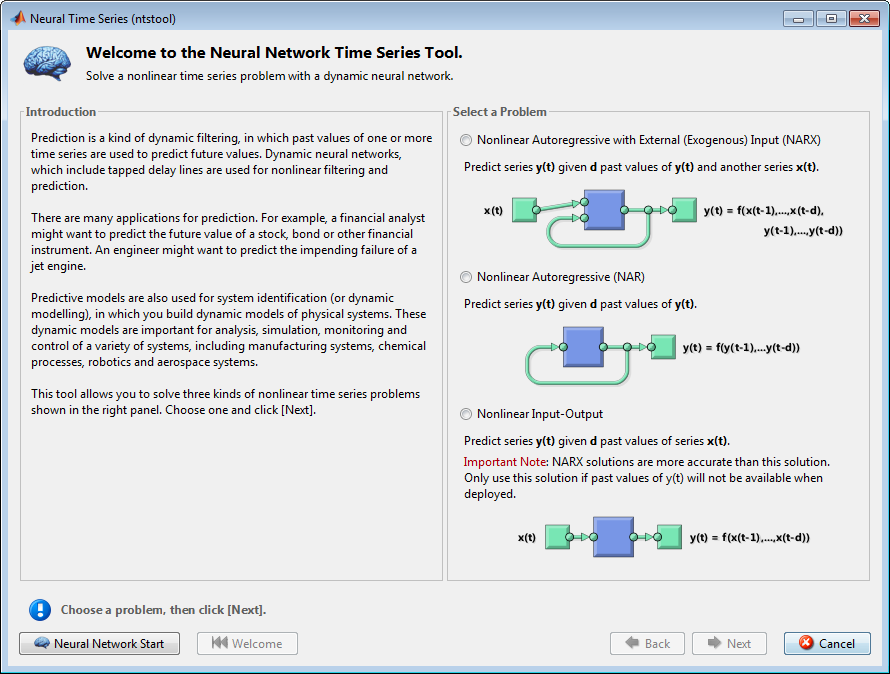
Заметьте, что эта вводная панель отличается, чем вводные панели для других графический интерфейсов пользователя. Это вызвано тем, что ntstool может использоваться, чтобы решить три различных видов проблем временных рядов.
В первом типе проблемы временных рядов требуется предсказать будущие значения временных рядов y (t) от прошлых значений тех временных рядов и прошлых значений серии x второго раза (t). Эта форма прогноза называется нелинейная авторегрессивный с внешним (внешним) входом или NARX (см. “Сеть NARX” (narxnet, closeloop)), и может быть записан можно следующим образом:
y (t) = f (y (t – 1)..., y (t – d), x (t – 1)..., (t – d))
Эта модель могла использоваться, чтобы предсказать будущие значения запаса или связи, на основе таких экономических переменных как показатели безработицы, GDP, и т.д. Это могло также использоваться в системе идентификации, в которой модели разрабатываются, чтобы представлять динамические системы, такие как химические процессы, производственные системы, робототехника, космические транспортные средства, и т.д.
Во втором типе проблемы временных рядов существует только один включенный ряд. Будущие значения временных рядов y (t) предсказаны только от прошлых значений того ряда. Эта форма прогноза называется нелинейная авторегрессивный, или NAR и может быть записана можно следующим образом:
y (t) = f (y (t – 1)..., y (t – d))
Эта модель могла также использоваться, чтобы предсказать финансовые инструменты, но без использования сопутствующего ряда.
Третья проблема временных рядов похожа на первый тип, в тех двух рядах включены, входная серия x (t) и серия y выхода/цели (t). Здесь вы хотите предсказать значения y (t) от предыдущих значений x (t), но без ведома предыдущих значений y (t). Эта модель ввода/вывода может быть записана можно следующим образом:
y (t) = f (x (t – 1)..., x (t – d))
Модель NARX предоставит лучшие прогнозы, чем эта модель ввода - вывода, потому что это использует дополнительную информацию, содержавшуюся в предыдущих значениях y (t). Однако могут быть некоторые приложения, в которых предыдущие значения y (t) не были бы доступны. Те - единственные случаи, где вы хотели бы использовать модель ввода - вывода вместо модели NARX.
В данном примере выберите модель NARX и нажмите Далее, чтобы продолжить.
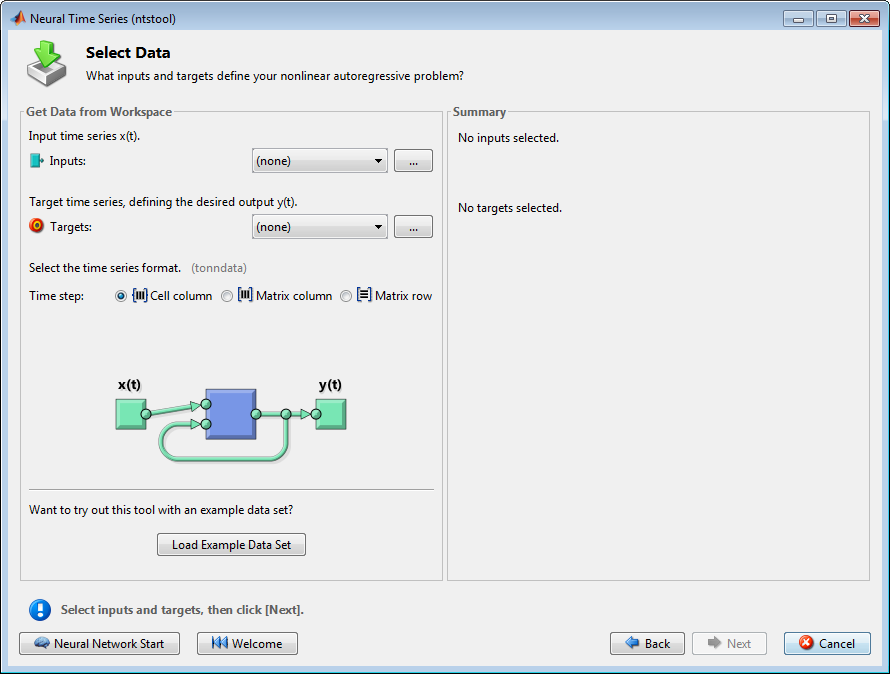
Нажмите Load Example Data Set в окне Select Data. Окно Time Series Data Set Chooser открывается.
Используйте Входные параметры и Целевые опции в окне Select Data, когда необходимо будет загрузить данные из рабочей области MATLAB®.
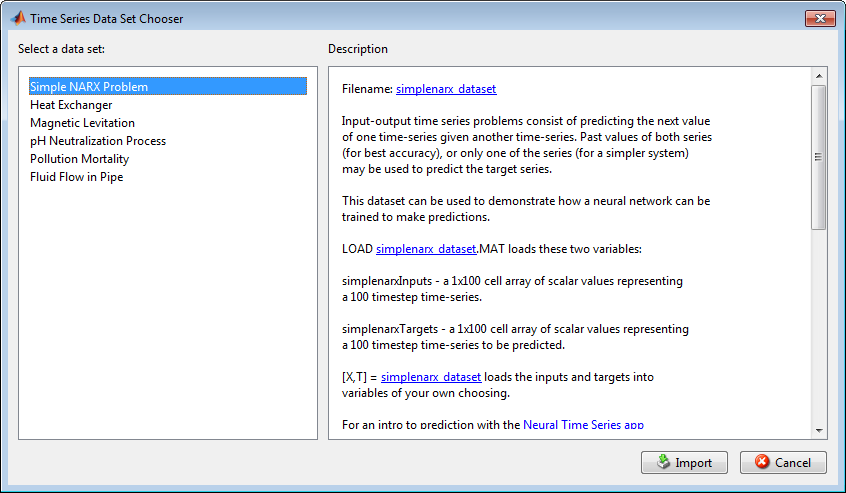
Выберите Процесс Нейтрализации pH и нажмите Import. Это возвращает вас в окно Select Data.
Нажмите Далее, чтобы открыть окно Validation и Test Data, показанное в следующем рисунке.
Валидация и наборы тестовых данных каждый установлены в 15% исходных данных.
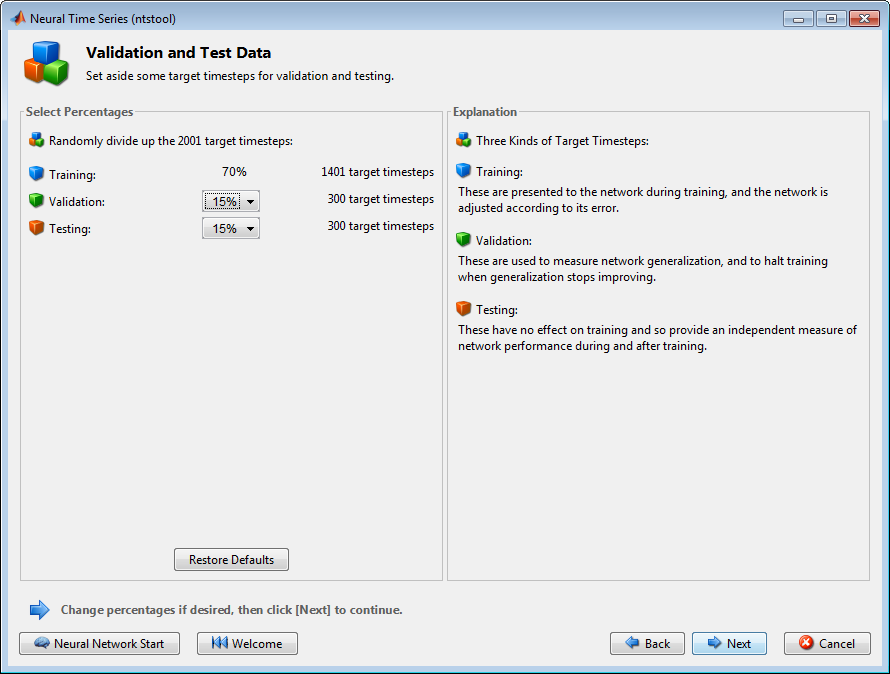
С этими настройками входные векторы и целевые векторы будут случайным образом разделены на три набора можно следующим образом:
70% будут использоваться в обучении.
15% будут использоваться, чтобы подтвердить это, сеть делает вывод и остановить обучение перед сверхподбором кривой.
Последние 15% будут использоваться в качестве абсолютно независимого теста сетевого обобщения.
(См. “Деление Данных” для большего количества обсуждения процесса деления данных.)
Нажать Далее.
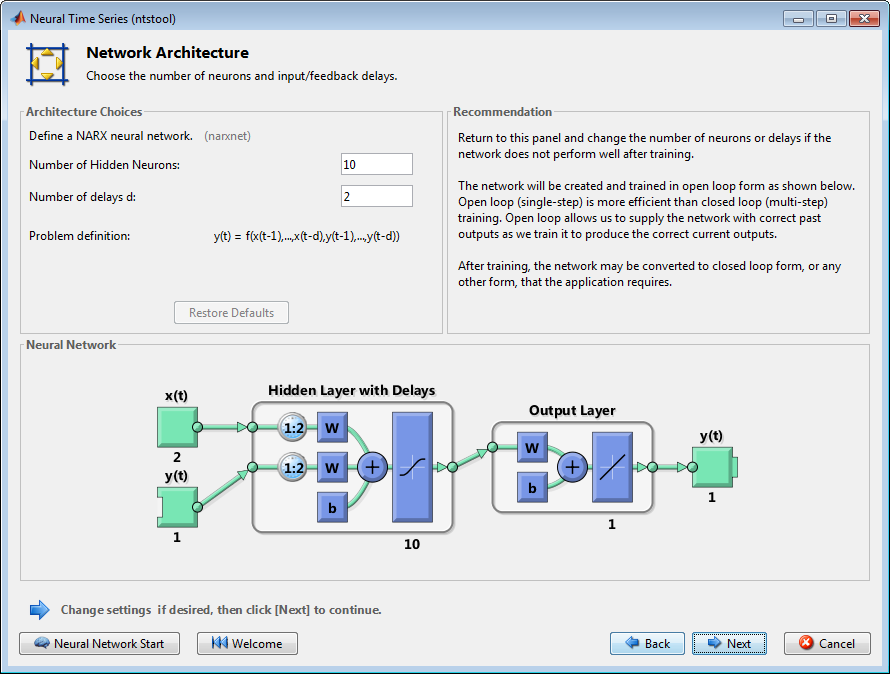
Стандартная сеть NARX является 2D слоем сеть feedforward с сигмоидальной передаточной функцией в скрытом слое и линейной передаточной функцией в выходном слое. Эта сеть также использует коснувшиеся линии задержки, чтобы сохранить предыдущие значения x (t) и y (t) последовательности. Обратите внимание на то, что выход сети NARX, y (t), возвращен к входу сети (через задержки), поскольку y (t) является функцией y (t – 1), y (t – 2)..., y (t – d). Однако для эффективного обучения эта обратная связь может быть открыта.
Поскольку истинный выход доступен во время обучения сети, можно использовать архитектуру разомкнутого цикла, показанную выше, в котором истинный выход используется вместо того, чтобы возвратить предполагаемый выход. Это имеет два преимущества. Прежде всего, вход к сети feedforward более точен. Второе - то, что получившаяся сеть имеет просто архитектура feedforward, и поэтому более эффективный алгоритм может использоваться в обучении. Эта сеть обсуждена более подробно в “Сети NARX” (narxnet, closeloop).
Номер по умолчанию скрытых нейронов определяется к 10. Количество по умолчанию задержек равняется 2. Измените это значение в 4. Вы можете хотеть настроить эти числа, если сетевая производительность обучения плоха.
Нажать Далее.
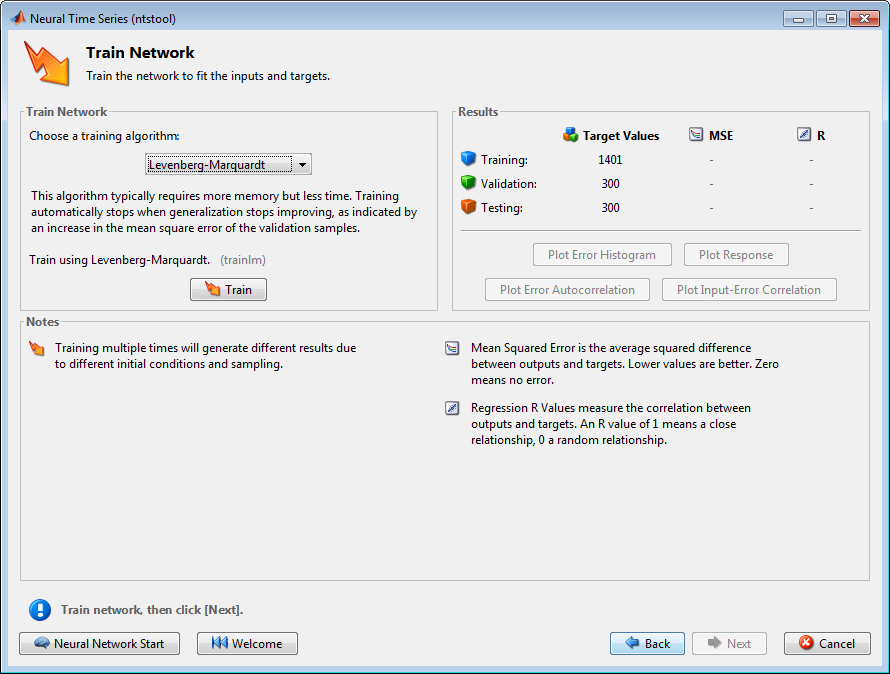
Выберите учебный алгоритм, затем нажмите Train. Levenberg-Marquardt (trainlm) рекомендуется для большинства проблем, но для некоторых шумных и небольших проблем Байесова Регуляризация (trainbr) может занять больше времени, но получить лучшее решение. Для больших проблем, однако, Масштабированный Метод сопряженных градиентов (trainscg) рекомендуется, когда это использует вычисления градиента, которые являются большей памятью, эффективной, чем якобиевские вычисления другие два использования алгоритмов. Этот пример использует Levenberg-Marquardt по умолчанию.
Обучению, продолженному до ошибки валидации, не удалось уменьшиться для шести итераций (остановка валидации).
В соответствии с Графиками, нажмите Error Autocorrelation. Это используется, чтобы подтвердить производительность сети.
Следующий график отображает ошибочную автокорреляционную функцию. Это описывает, как ошибки прогноза связаны вовремя. Для совершенной модели прогноза должно только быть одно ненулевое значение автокорреляционной функции, и это должно произойти в нулевой задержке. (Это - среднеквадратичная погрешность.) Это означало бы, что ошибки прогноза были абсолютно некоррелироваными друг с другом (белый шум). Если бы была значительная корреляция по ошибкам прогноза, то должно быть возможно улучшить прогноз - возможно, путем увеличения числа задержек коснувшихся линий задержки. В этом случае корреляции, за исключением той в нулевой задержке, падают приблизительно в 95% пределов достоверности вокруг нуля, таким образом, модель, кажется, соответствует. Если бы еще более точные результаты требовались, вы могли бы переобучить сеть путем нажатия на Retrain in ntstool. Это изменит начальные веса и смещения сети, и может произвести улучшенную сеть после переквалификации.
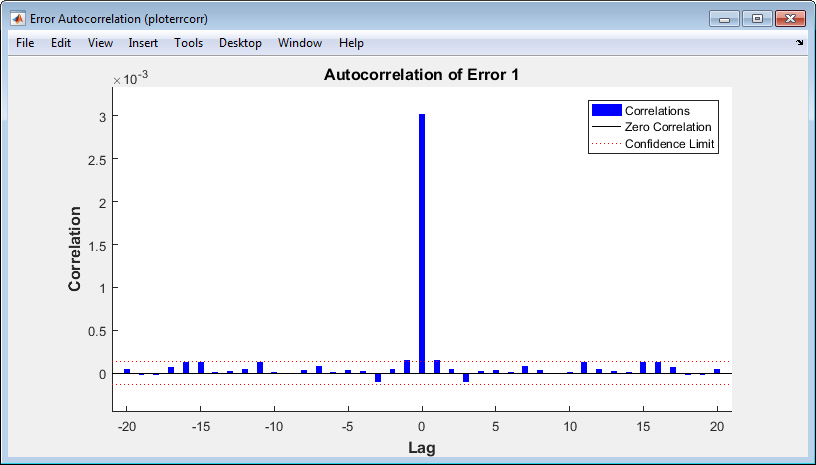
Просмотрите функцию взаимной корреляции входной ошибки, чтобы получить дополнительную верификацию производительности сети. Под панелью Графиков нажмите Input-Error Cross-correlation.
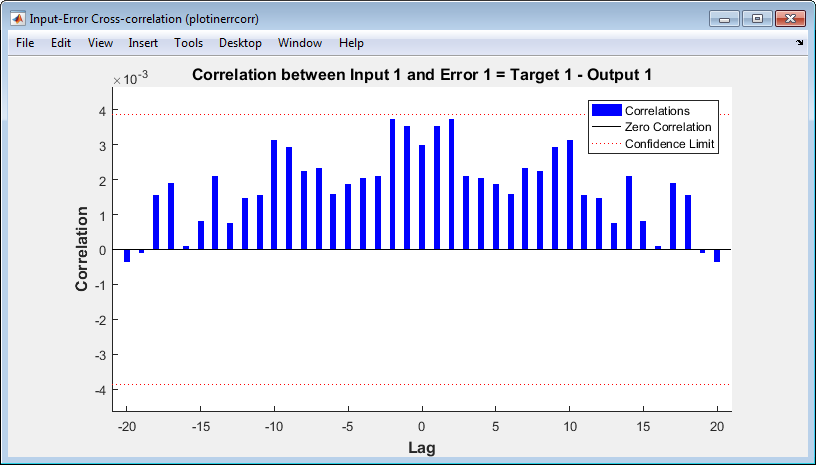
Эта функция взаимной корреляции входной ошибки иллюстрирует, как ошибки коррелируются с входной последовательностью x (t). Для совершенной модели прогноза все корреляции должны быть нулем. Если вход коррелируется с ошибкой, то должно быть возможно улучшить прогноз, возможно, путем увеличения числа задержек коснувшихся линий задержки. В этом случае все корреляции находятся в пределах доверительных границ вокруг нуля.
В соответствии с Графиками, нажмите Time Series Response. Это отображает входные параметры, цели и ошибки по сравнению со временем. Это также указывает, какие моменты времени были выбраны для обучения, тестирования и валидации.
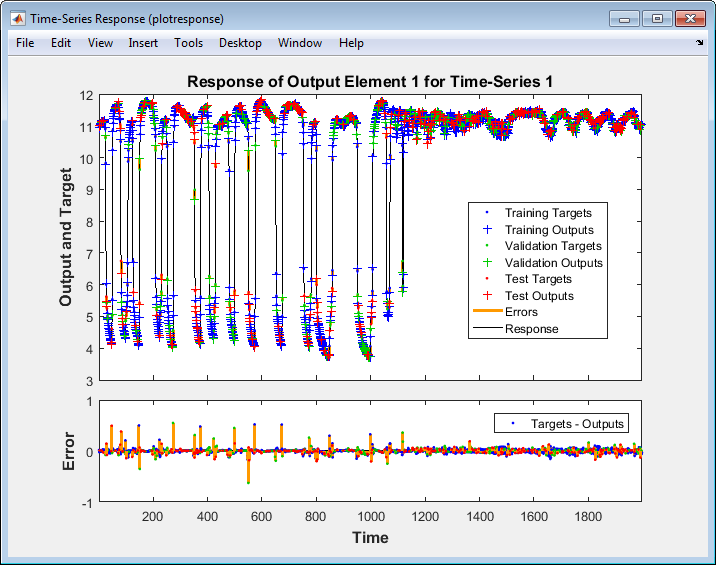
Нажмите Далее в Приложении Временных рядов Нейронной сети, чтобы оценить сеть.
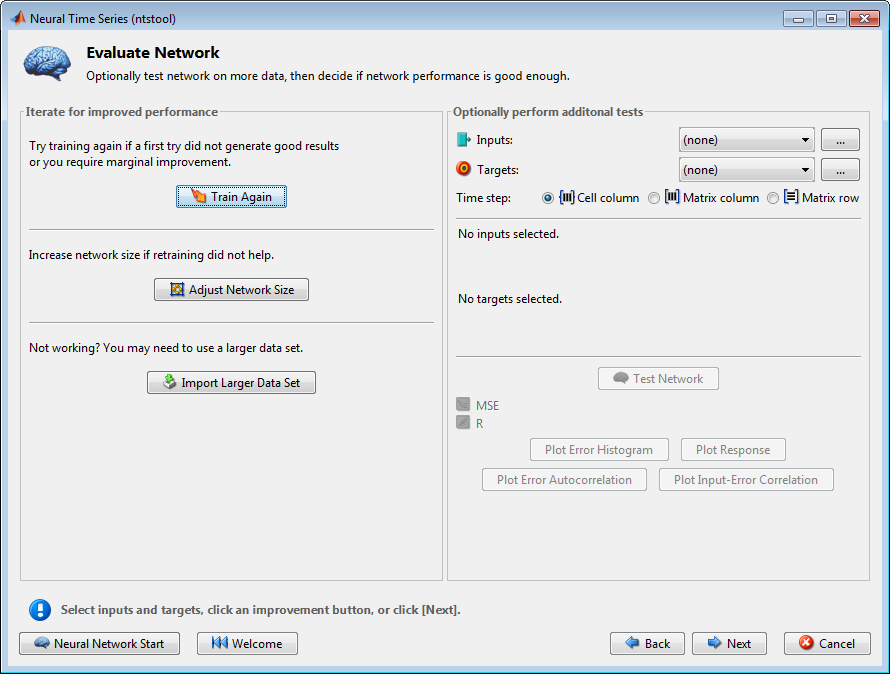
На данном этапе можно протестировать сеть против новых данных.
Если вы неудовлетворены производительностью сети на исходных или новых данных, можно сделать любое следующее:
Обучите его снова.
Увеличьте число нейронов и/или количество задержек.
Получите больший обучающий набор данных.
Если производительность на наборе обучающих данных хороша, но производительность набора тестов значительно хуже, который мог указать на сверхподбор кривой, то сокращение количества нейронов может улучшить ваши результаты.
Если вы удовлетворены производительностью сети, нажимаете Далее.
Используйте эту панель, чтобы сгенерировать функцию MATLAB или схему Simulink® для симуляции вашей нейронной сети. Можно использовать сгенерированный код или схематически изобразить, чтобы лучше изучить, как нейронная сеть вычисляет выходные параметры из входных параметров, или разверните сеть с инструментами MATLAB Compiler™ и другим MATLAB и инструментами генерации кода Simulink.
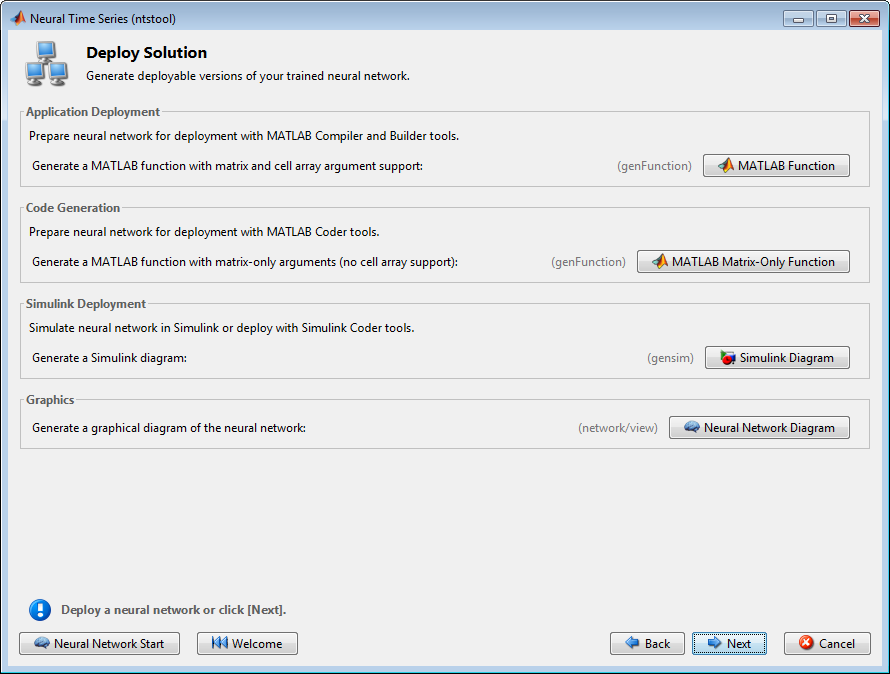
Используйте кнопки на этом экране, чтобы сгенерировать скрипты или сохранить ваши результаты.
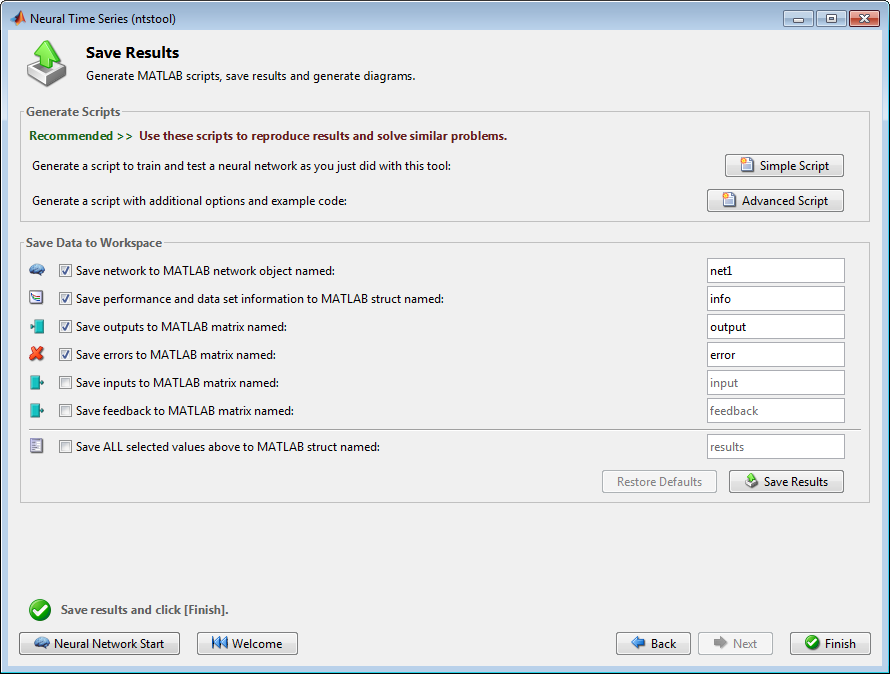
Можно нажать Simple Script или Advanced Script, чтобы создать код MATLAB, который может использоваться, чтобы воспроизвести все предыдущие шаги от командной строки. Создание кода MATLAB может быть полезным, если вы хотите изучить, как использовать функциональность командной строки тулбокса, чтобы настроить учебный процесс. В Использовании Функций Командной строки вы исследуете сгенерированные скрипты более подробно.
У вас может также быть сеть, сохраненная как net в рабочей области. Можно выполнить дополнительные тесты на нем или поместить его, чтобы работать над новыми входными параметрами.
После создания кода MATLAB и сохранения ваших результатов, нажмите Finish.
Самый легкий способ изучить, как использовать функциональность командной строки тулбокса, состоит в том, чтобы сгенерировать скрипты от графический интерфейсов пользователя, и затем изменить их, чтобы настроить сетевое обучение. Как пример, посмотрите на простой скрипт, который был создан на шаге 15 предыдущего раздела.
% Solve an Autoregression Problem with External % Input with a NARX Neural Network % Script generated by NTSTOOL % % This script assumes the variables on the right of % these equalities are defined: % % phInputs - input time series. % phTargets - feedback time series. inputSeries = phInputs; targetSeries = phTargets; % Create a Nonlinear Autoregressive Network with External Input inputDelays = 1:4; feedbackDelays = 1:4; hiddenLayerSize = 10; net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize); % Prepare the Data for Training and Simulation % The function PREPARETS prepares time series data % for a particular network, shifting time by the minimum % amount to fill input states and layer states. % Using PREPARETS allows you to keep your original % time series data unchanged, while easily customizing it % for networks with differing numbers of delays, with % open loop or closed loop feedback modes. [inputs,inputStates,layerStates,targets] = ... preparets(net,inputSeries,{},targetSeries); % Set up Division of Data for Training, Validation, Testing net.divideParam.trainRatio = 70/100; net.divideParam.valRatio = 15/100; net.divideParam.testRatio = 15/100; % Train the Network [net,tr] = train(net,inputs,targets,inputStates,layerStates); % Test the Network outputs = net(inputs,inputStates,layerStates); errors = gsubtract(targets,outputs); performance = perform(net,targets,outputs) % View the Network view(net) % Plots % Uncomment these lines to enable various plots. % figure, plotperform(tr) % figure, plottrainstate(tr) % figure, plotregression(targets,outputs) % figure, plotresponse(targets,outputs) % figure, ploterrcorr(errors) % figure, plotinerrcorr(inputs,errors) % Closed Loop Network % Use this network to do multi-step prediction. % The function CLOSELOOP replaces the feedback input with a direct % connection from the output layer. netc = closeloop(net); netc.name = [net.name ' - Closed Loop']; view(netc) [xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries); yc = netc(xc,xic,aic); closedLoopPerformance = perform(netc,tc,yc) % Early Prediction Network % For some applications it helps to get the prediction a % timestep early. % The original network returns predicted y(t+1) at the same % time it is given y(t+1). % For some applications such as decision making, it would % help to have predicted y(t+1) once y(t) is available, but % before the actual y(t+1) occurs. % The network can be made to return its output a timestep early % by removing one delay so that its minimal tap delay is now % 0 instead of 1. The new network returns the same outputs as % the original network, but outputs are shifted left one timestep. nets = removedelay(net); nets.name = [net.name ' - Predict One Step Ahead']; view(nets) [xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries); ys = nets(xs,xis,ais); earlyPredictPerformance = perform(nets,ts,ys)
Можно сохранить скрипт, и затем запустить его из командной строки, чтобы воспроизвести результаты предыдущего сеанса графический интерфейса пользователя. Можно также отредактировать скрипт, чтобы настроить учебный процесс. В этом случае выполните каждый из шагов в скрипте.
Скрипт принимает, что входные векторы и целевые векторы уже загружаются в рабочую область. Если данные не загружаются, можно загрузить их можно следующим образом:
load ph_dataset
inputSeries = phInputs;
targetSeries = phTargets;
Создайте сеть. Сеть NARX, narxnet, сеть feedforward с коричнево-сигмоидальной передаточной функцией по умолчанию в скрытом слое и линейной передаточной функцией в выходном слое. Эта сеть имеет два входных параметров. Каждый - внешний вход, и другой связь обратной связи от сетевого выхода. (После того, как сеть была обучена, эта связь обратной связи может быть закрыта, как вы будете видеть на более позднем шаге.) Для каждых из этих входных параметров, существует коснувшаяся линия задержки, чтобы сохранить предыдущие значения. Чтобы присвоить сетевую архитектуру для сети NARX, необходимо выбрать задержки, сопоставленные с каждой коснувшейся линией задержки, и также количеством нейронов скрытого слоя. В следующих шагах вы присваиваете входные задержки и задержки обратной связи, чтобы лежать в диапазоне от 1 до 4 и количество скрытых нейронов, чтобы быть 10.
inputDelays = 1:4; feedbackDelays = 1:4; hiddenLayerSize = 10; net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);
Увеличение числа нейронов и количества задержек требует большего количества расчета, и это имеет тенденцию сверхсоответствовать данным, когда номера определяются слишком высоко, но это позволяет сети решать более сложные задачи. Больше слоев требует большего количества расчета, но их использование может привести к сети, решающей комплексные задачи более эффективно. Чтобы использовать больше чем один скрытый слой, введите размеры скрытого слоя как элементы массива в fitnet команда.
Подготовьте данные к обучению. Когда обучение сеть, содержащая коснувшиеся линии задержки, необходимо заполнить задержки начальными значениями вводов и выводов сети. Существует команда тулбокса, которая упрощает этот процесс - preparets. Эта функция имеет три входных параметра: сеть, входная последовательность и целевая последовательность. Функция возвращает начальные условия, которые необходимы, чтобы заполнить коснувшиеся линии задержки в сети, и измененный вход и целевые последовательности, куда начальные условия были удалены. Можно вызвать функцию можно следующим образом:
[inputs,inputStates,layerStates,targets] = ...
preparets(net,inputSeries,{},targetSeries);
Создайте деление данных.
net.divideParam.trainRatio = 70/100; net.divideParam.valRatio = 15/100; net.divideParam.testRatio = 15/100;
С этими настройками входные векторы и целевые векторы будут случайным образом разделены, с 70%, используемыми в обучении, 15% для валидации и 15% для тестирования.
Обучите сеть. Сеть использует алгоритм Levenberg-Marquardt по умолчанию (trainlm) для обучения. Для проблем, в которых Levenberg-Marquardt не производит, когда точные результаты, как желаемый, или для больших проблем данных, рассматривают установку сетевой учебной функции к Байесовой Регуляризации (trainbr) или масштабированный метод сопряженных градиентов (trainscg), соответственно, с также
net.trainFcn = 'trainbr'; net.trainFcn = 'trainscg';
Обучать сеть, введите:
[net,tr] = train(net,inputs,targets,inputStates,layerStates);
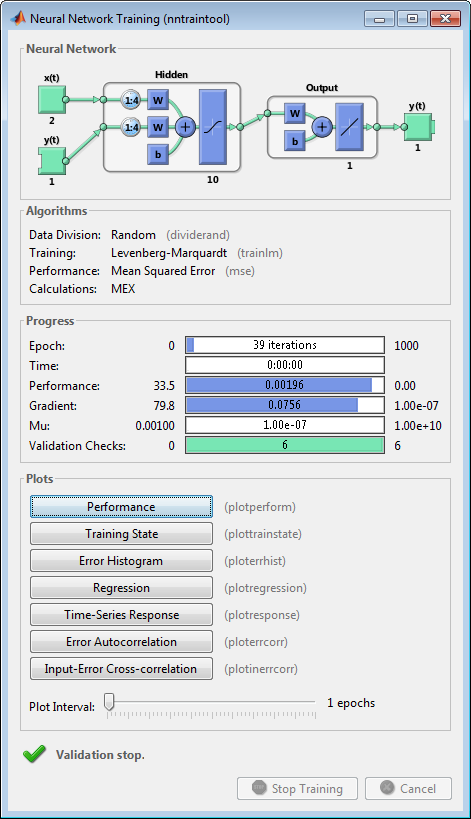
Во время обучения открывается следующее учебное окно. Это окно отображает прогресс обучения и позволяет вам прерывать обучение в любой точке путем нажатия на Stop Training.
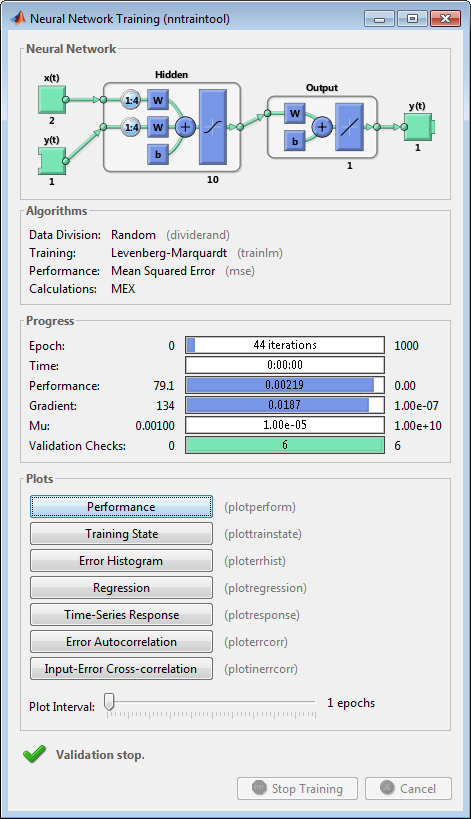
Это обучение остановилось, когда ошибка валидации увеличилась для шести итераций, которые произошли в итерации 44.
Протестируйте сеть. После того, как сеть была обучена, можно использовать ее, чтобы вычислить сетевые выходные параметры. Следующий код вычисляет сетевые выходные параметры, ошибки и общую производительность. Обратите внимание на то, что, чтобы симулировать сеть с коснувшимися линиями задержки, необходимо присвоить начальные значения для этих задержанных сигналов. Это сделано с inputStates и layerStates если preparets в более ранней стадии.
outputs = net(inputs,inputStates,layerStates); errors = gsubtract(targets,outputs); performance = perform(net,targets,outputs)
performance =
0.0042
Просмотрите сетевой график.
view(net)

Постройте запись обучения производительности, чтобы проверять на потенциальный сверхподбор кривой.
figure, plotperform(tr)

Этот рисунок показывает что обучение и ошибочное уменьшение валидации до подсвеченной эпохи. Не кажется, что любой сверхподбор кривой произошел, потому что ошибка валидации не увеличивается перед этой эпохой.
Все обучение сделано в разомкнутом цикле (также названный последовательно-параллельной архитектурой), включая валидацию и тестирующие шаги. Типичный рабочий процесс должен полностью создать сеть в разомкнутом цикле, и только когда это было обучено (который включает валидацию, и тестирующие шаги) преобразованный к замкнутому циклу для многоступенчатого вперед прогноза. Аналогично, R значения в графический интерфейсе пользователя вычисляются на основе результатов обучения разомкнутого цикла.
Замкните круг в сети NARX. Когда обратная связь открыта в сети NARX, она выполняет прогноз "один шаг вперед". Это предсказывает следующее значение y (t) от предыдущих значений y (t) и x (t). С закрытой обратной связью это может использоваться, чтобы выполнить многоступенчатые вперед прогнозы. Это вызвано тем, что прогнозы y (t) будут использоваться вместо фактических будущих значений y (t). Следующие команды могут использоваться, чтобы замкнуть круг и вычислить производительность с обратной связью
netc = closeloop(net);
netc.name = [net.name ' - Closed Loop'];
view(netc)
[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);
yc = netc(xc,xic,aic);
perfc = perform(netc,tc,yc)
perfc =
2.8744

Удалите задержку из сети, чтобы получить прогноз один временной шаг рано.
nets = removedelay(net);
nets.name = [net.name ' - Predict One Step Ahead'];
view(nets)
[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);
ys = nets(xs,xis,ais);
earlyPredictPerformance = perform(nets,ts,ys)
earlyPredictPerformance =
0.0042

От этого рисунка вы видите, что сеть идентична предыдущей сети разомкнутого цикла, за исключением того, что одна задержка была удалена из каждой из коснувшихся линий задержки. Выходом сети является затем y (t + 1) вместо y (t). Это может иногда быть полезно, когда сеть развертывается для определенных приложений.
Если производительность сети не является удовлетворительной, вы могли бы попробовать любой из этих подходов:
Сбросьте начальные сетевые веса и смещения к новым значениям с init и обучайтесь снова (см. “Веса Инициализации” (init)).
Увеличьте число скрытых нейронов или количество задержек.
Увеличьте число учебных векторов.
Увеличьте число входных значений, если более релевантная информация доступна.
Попробуйте различный учебный алгоритм (см. “Учебные Алгоритмы”).
Чтобы получить больше опыта в операциях командной строки, попробуйте некоторые из этих задач:
Во время обучения, открытого окно графика (такое как ошибочный график корреляции), и, смотрят, что он анимирует.
Постройте из командной строки с функциями, такими как plotresponse, ploterrcorr и plotperform. (Для получения дополнительной информации об использовании этих функций смотрите их страницы с описанием.)
Кроме того, см. усовершенствованный скрипт для большего количества опций, когда обучение из командной строки.
Каждый раз нейронная сеть обучена, может привести к различному решению из-за различного начального веса и сместить значения и различные деления данных в обучение, валидацию и наборы тестов. В результате различные нейронные сети, обученные на той же проблеме, могут дать различные выходные параметры для того же входа. Чтобы гарантировать, что нейронная сеть хорошей точности была найдена, переобучайтесь несколько раз.
Существует несколько других методов для того, чтобы улучшить начальные решения, если более высокая точность желаема. Для получения дополнительной информации смотрите, Улучшают Мелкое Обобщение Нейронной сети и Стараются не Сверхсоответствовать.