Оцените мультипликативную модель ARIMA Используя приложение Econometric Modeler

В этом примере показано, как оценить мультипликативную сезонную модель ARIMA при помощи приложения Econometric Modeler. Набор данных, который хранится в mlr/examples/econ/Data_Airline.mat, содержит ежемесячные количества авиапассажиров. Папка mlr значение matlabroot.

Импортируйте данные в Econometric Modeler

В командной строке загрузите Data_Airline.mat набор данных.

load(fullfile(matlabroot,'examples','econ','Data_Airline.mat'))

В командной строке откройте приложение Econometric Modeler.

econometricModeler

В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).

Импортируйте DataTable в приложение:

На вкладке Econometric Modeler, в разделе Import, нажатии кнопки.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для DataTable переменная.
Нажмите Import.

Переменная PSSG появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSG).

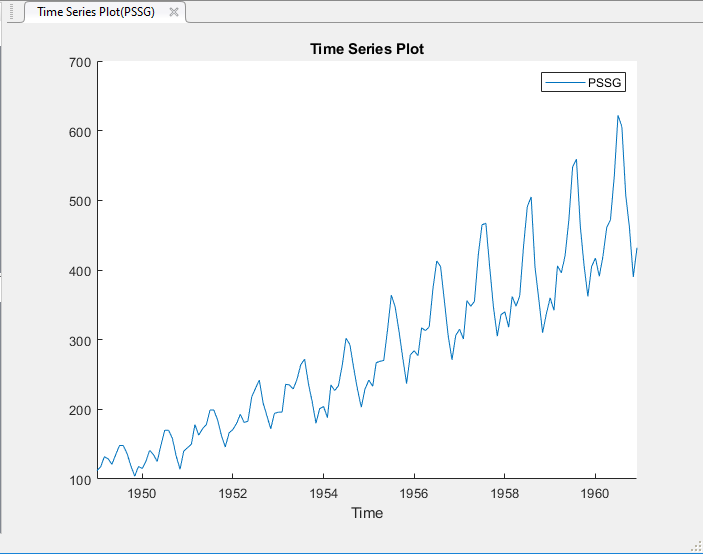
Ряд показывает сезонный тренд, последовательную корреляцию и возможный экспоненциальный рост. Для интерактивного анализа последовательной корреляции смотрите, Обнаруживают Последовательную Корреляцию Используя Приложение Econometric Modeler.

Стабилизируйте ряд

Обратитесь к экспоненциальному тренду путем применяния логарифмического преобразования к PSSG.

В Data Browser выберите PSSG.
На вкладке Econometric Modeler, в разделе Transforms, нажимают Log.

Преобразованная переменная PSSGLog появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSGLog).

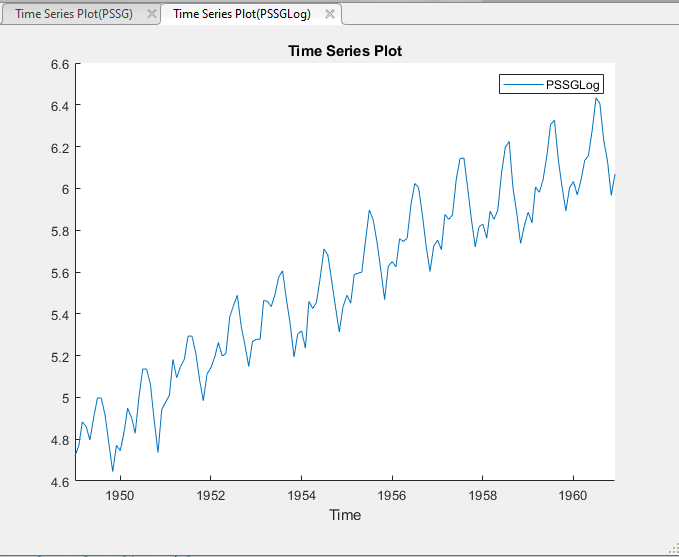
Экспоненциальный рост, кажется, удален из ряда.

Обратитесь к сезонному тренду путем применения 12-го порядка сезонное различие. С PSSGLog выбранный в Data Browser, на вкладке Econometric Modeler, в разделе Transforms, устанавливает Seasonal на 12. Затем нажмите Seasonal.

Преобразованная переменная PSSGLogSeasonalDiff появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSGLogSeasonalDiff).

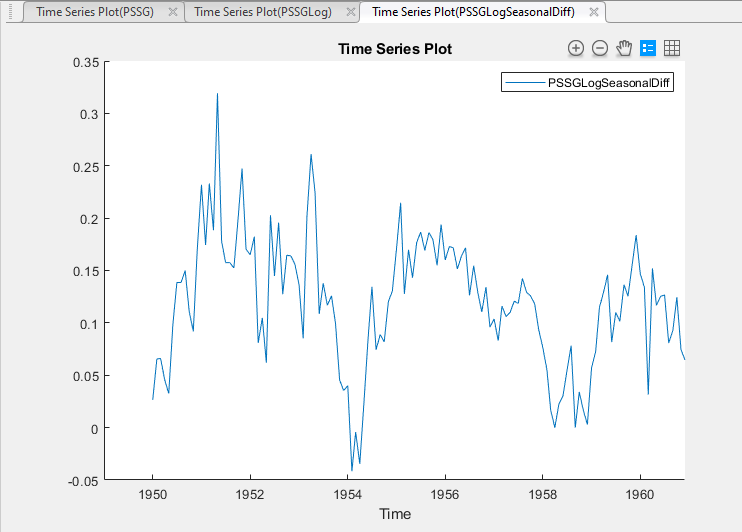
Преобразованный ряд, кажется, имеет модульный корень.

Протестируйте нулевую гипотезу что PSSGLogSeasonalDiff имеет модульный корень при помощи Увеличенного Более полного Дики теста. Укажите, что альтернатива является моделью AR (0), затем протестируйте снова определение модели AR (1). Настройте уровень значения к 0,025, чтобы обеспечить общий уровень значения 0,05.

С PSSGLogSeasonalDiff выбранный в Data Browser, на вкладке Econometric Modeler, в разделе Tests, нажимают New Test> Augmented Dickey-Fuller Test.
На вкладке ADF, в разделе Parameters, устанавливает Significance Level на 0.025.
В разделе Tests нажмите Run Test.
В разделе Parameters, набор Number of Lags к 1.
В разделе Tests нажмите Run Test.

Результаты испытаний появляются в таблице Results документа ADF(PSSGLogSeasonalDiff).

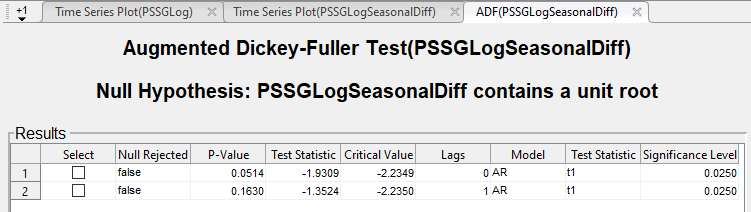
Обоим тестам не удается отклонить нулевую гипотезу, что ряд является модульным корневым процессом.

Обратитесь к модульному корню путем применения первого различия для PSSGLogSeasonalDiff. С PSSGLogSeasonalDiff выбранный в Data Browser, кликните по вкладке Econometric Modeler. Затем в разделе Transforms нажмите Difference.

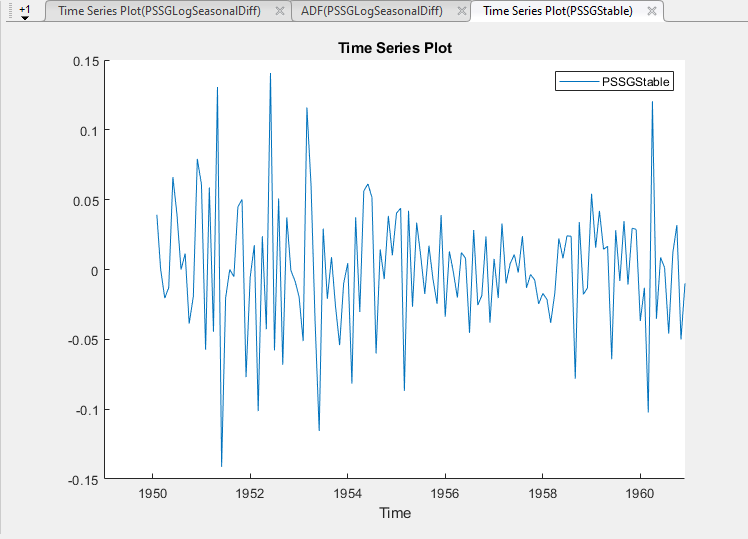
Преобразованная переменная PSSGLogSeasonalDiffDiff появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSGLogSeasonalDiffDiff).

Переименуйте PSSGLogSeasonalDiffDiff переменная к PSSGStable:

В Data Browser щелкните правой кнопкой по PSSGLogSeasonalDiffDiff.
В контекстном меню выберите Rename.
Введите PSSGStable.

Обновления приложения имена всех документов сопоставлены с преобразованным рядом.

Идентифицируйте модель для ряда

Определите структуру задержки для условной средней модели данных путем графического вывода демонстрационной автокорреляционной функции (ACF) и частичная автокорреляционная функция (PACF).

С PSSGStable выбранный в Data Browser, кликните по вкладке Plots, затем нажмите ACF.
Покажите первые 50 задержек ACF. На вкладке ACF, набор Number of Lags к 50.
Кликните по вкладке Plots, затем нажмите PACF.
Покажите первые 50 задержек PACF. На вкладке PACF, набор Number of Lags к 50.
Перетащите окно рисунка ACF(PSSGStable) выше окна рисунка PACF(PSSGStable).

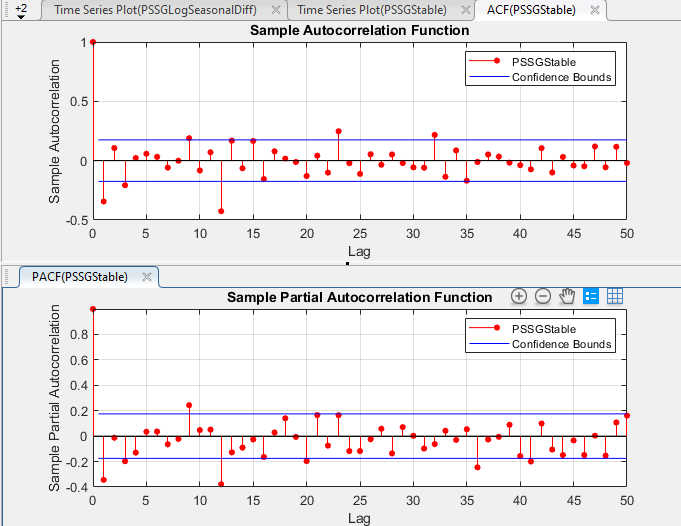
Согласно [1], автокорреляции в ACF и PACF предполагают, что следующий SARIMA (0,1,1) × (0,1,1) ₁₂ моделей подходит для PSSGLog.

$(1 - L) (1 - L^{12}) y_{t} = (1 + θ_{1} L) (1 + Θ_{12} L^{12}) ε_{t} .$

Закройте все окна рисунка.

Задайте и оцените модель SARIMA

Задайте SARIMA (0,1,1) × (0,1,1) ₁₂ моделей.

В Data Browser выберите PSSGLog временные ряды.
На вкладке Econometric Modeler, в разделе Models, кликают по стреле> SARIMA.
В диалоговом окне SARIMA Model Parameters, на вкладке Lag Order:
- Раздел Nonseasonal
  1. Установите Degrees of Integration на 1.
  2. Установите Moving Average Order на 1.
  3. Снимите флажок Include Constant Term.
- Раздел Seasonal
  1. Установите Period на 12 указать на ежемесячные данные.
  2. Установите Moving Average Order на 1.
  3. Установите флажок Include Seasonal Difference.
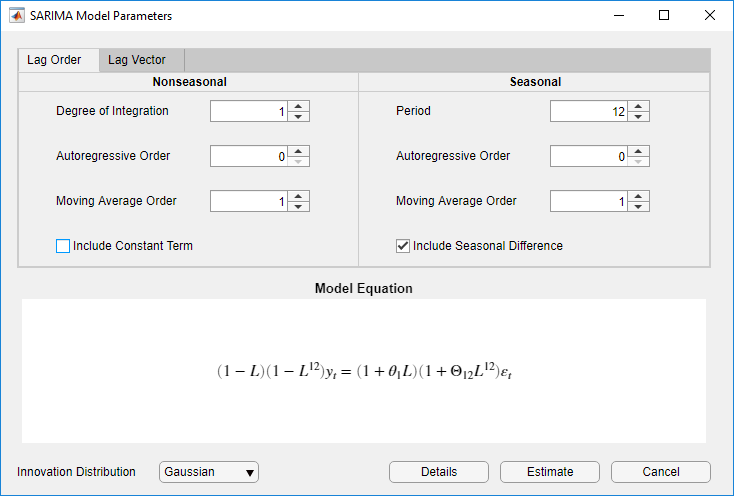
Нажмите Estimate.

Переменная SARIMA_PSSGLog модели появляется в Data Browser, и его сводные данные оценки появляются в документе Model Summary(SARIMA_PSSGLog).

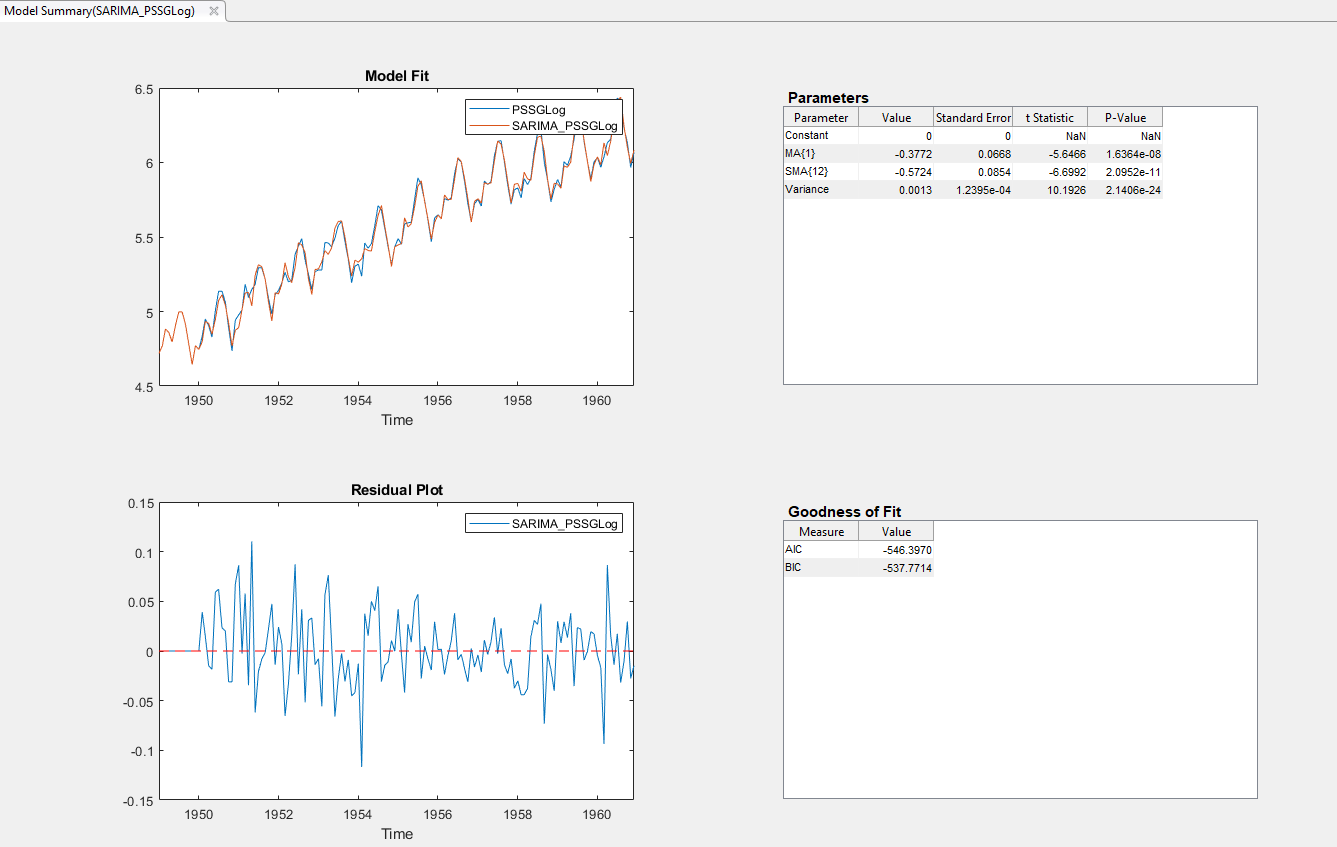
Результаты включают:

Model Fit — График временных рядов PSSGLog и подходящие значения от SARIMA_PSSGLog.
Residual Plot — График временных рядов остаточных значений SARIMA_PSSGLog.
Параметры Таблица предполагаемых параметров SARIMA_PSSGLog. Поскольку постоянный термин считался зафиксированный к 0 во время оценки, ее значение и стандартная погрешность 0.
Goodness of Fit — AIC и BIC соответствуют статистике SARIMA_PSSGLog.

Ссылки

[1] Поле, G. E. P. Г. М. Дженкинс и Г. К. Рейнсель. Анализ Временных Рядов: Прогнозирование и Управление. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1994.

Смотрите также

Документация