Годограф Найквиста частотной характеристики
nyquist(sys)
nyquist(sys,w)
nyquist(sys1,sys2,...,sysN)
nyquist(sys1,sys2,...,sysN,w)
nyquist(sys1,'PlotStyle1',...,sysN,'PlotStyleN')
[re,im,w] = nyquist(sys)
[re,im]
= nyquist(sys,w)
[re,im,w,sdre,sdim] = nyquist(sys)
nyquist создает годограф Найквиста частотной характеристики модели динамической системы. Когда вызвано без левых аргументов, nyquist производит годограф Найквиста на экране. Годографы Найквиста используются, чтобы анализировать системные свойства включая запас по амплитуде, запас по фазе и устойчивость.
nyquist(sys) создает годограф Найквиста динамической системы sys. Эта модель может быть непрерывной или дискретной, и SISO или MIMO. В случае MIMO, nyquist производит массив годографов Найквиста, каждый график, показывающий ответ одного конкретного канала ввода-вывода. Точки частоты выбраны автоматически на основе системных полюсов и нулей.
nyquist(sys,w) явным образом задает частотный диапазон или точки частоты, которые будут использоваться в графике. Чтобы фокусироваться на конкретном интервале частоты, установите w = {wmin,wmax}. Чтобы использовать конкретные точки частоты, установите w к вектору желаемых частот. Используйте logspace сгенерировать логарифмически распределенные векторы частоты. Частоты должны быть в rad/TimeUnit, где TimeUnit единицы измерения времени входной динамической системы, заданной в TimeUnit свойство sys.
nyquist(sys1,sys2,...,sysN) или nyquist(sys1,sys2,...,sysN,w) накладывает годографы Найквиста нескольких моделей LTI на одной фигуре. Все системы должны иметь то же количество вводов и выводов, но могут в противном случае быть соединением непрерывных - и системы дискретного времени. Можно также задать отличительный цвет, LineStyle и/или маркер для каждого системного графика с синтаксисом nyquist(sys1,'PlotStyle1',...,sysN,'PlotStyleN').
[re,im,w] = nyquist(sys) и [re,im]
= nyquist(sys,w) возвратите действительные и мнимые части частотной характеристики на частотах w (в rad/TimeUnit). re и im трехмерные массивы (см. "Аргументы" ниже для деталей).
[re,im,w,sdre,sdim] = nyquist(sys) также возвращает стандартные отклонения re и im для идентифицированной системы sys.
Выходные аргументы re и im трехмерные массивы с размерностями
Для систем SISO, скаляры re(1,1,k) и im(1,1,k) действительные и мнимые части ответа на частоте ωk = w (k).
Для систем MIMO с передаточной функцией H (s), re(:,:,k) и im(:,:,k) дайте действительные и мнимые части H (jωk) (оба массива со столькими же строк сколько выходные параметры и столько же столбцов сколько входные параметры). Таким образом,
где hij является передаточной функцией от входа j до выхода i.
Создайте следующую передаточную функцию и постройте ее ответ Найквиста.
.
H = tf([2 5 1],[1 2 3]); nyquist(H)
nyquist функция может отобразить сетку M-кругов, которые являются контурами постоянной величины с обратной связью. M-круги заданы как местоположение комплексных чисел, где следующее количество является постоянным значением через частоту.
.
Здесь, ω является частотой в radians/TimeUnit, где TimeUnit модули системного времени, и G является набором комплексных чисел, которые удовлетворяют постоянному требованию к величине.
Чтобы отобразить сетку M-кругов, щелкните правой кнопкой по графику и выберите Grid. В качестве альтернативы используйте grid команда.
grid on
Вычислите стандартные отклонения действительных и мнимых частей частотной характеристики идентифицированной модели. Используйте эти данные, чтобы создать 3σ график неопределенности ответа.
Загрузите данные об оценке z2.
load iddata2 z2;
Идентифицируйте модель передаточной функции использование данных.
sys_p = tfest(z2,2);
Получите стандартные отклонения для действительных и мнимых частей частотной характеристики для набора 512 частот, w.
w = linspace(-10*pi,10*pi,512); [re,im,wout,sdre,sdim] = nyquist(sys_p,w);
Здесь re и im действительные и мнимые части частотной характеристики и sdre и sdim их стандартные отклонения, соответственно. Частоты в wout совпадают с частотами, которые вы задали в w.
Создайте годограф Найквиста, показывающий ответ и 3σ неопределенность.
re = squeeze(re); im = squeeze(im); sdre = squeeze(sdre); sdim = squeeze(sdim); plot(re,im,'b',re+3*sdre,im+3*sdim,'k:',re-3*sdre,im-3*sdim,'k:') xlabel('Real Axis'); ylabel('Imaginary Axis');
Можно изменить свойства графика, например, модули. Для получения информации о способах изменить свойства ваших графиков, смотрите Способы Настроить Графики (Control System Toolbox). Для наибольшей гибкости в настройке свойств графика используйте nyquistplot команда вместо nyquist.
Существует две опции изменения масштаба, доступные из контекстного меню, которые применяются в частности к годографам Найквиста:
Full View — Отсекает неограниченные ветви годографа Найквиста, но все еще включает критическую точку (–1, 0).
Zoom on (-1,0) — Изменения масштаба вокруг критической точки (–1,0). (К изменению масштаба критической точки доступа программно, используйте nyquistplot вместо этого.)
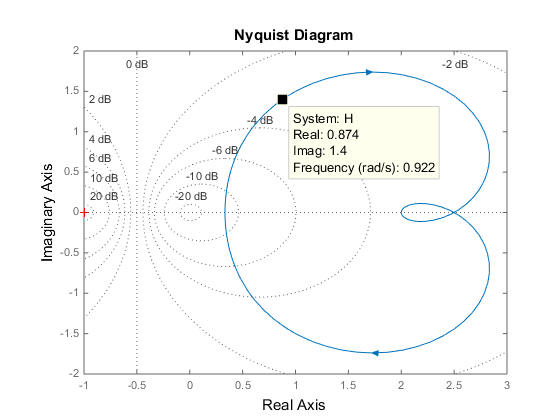
Чтобы активировать маркеры данных, которые отображают действительные и мнимые значения на данной частоте, щелкните где угодно на кривой. Следующий рисунок показывает nyquist постройте с маркером данных.
Смотрите bode.