Векторное произведение
C = cross( возвращает векторное произведение A,B)A и B.
Если A и B векторы, затем у них должна быть длина 3.
Если A и B матрицы или многомерные массивы, затем у них должен быть тот же размер. В этом случае, cross функционируйте обрабатывает A и B как наборы трехэлементных векторов. Функция вычисляет векторное произведение соответствующих векторов вдоль первого измерения массива, размер которого равняется 3.
Создайте два 3-D вектора.
A = [4 -2 1]; B = [1 -1 3];
Найдите векторное произведение A и B. Результат, C, вектор, который перпендикулярен обоим A и B.
C = cross(A,B)
C = 1×3
-5 -11 -2
Используйте скалярные произведения, чтобы проверить тот C перпендикулярно A и B.
dot(C,A)==0 & dot(C,B)==0
ans = logical
1
Результатом является логический 1 TRUE).
Создайте две матрицы, содержащие случайные целые числа.
A = randi(15,3,5)
A = 3×5
13 14 5 15 15
14 10 9 3 8
2 2 15 15 13
B = randi(25,3,5)
B = 3×5
4 20 1 17 10
11 24 22 19 17
23 17 24 19 5
Найдите векторное произведение A и B.
C = cross(A,B)
C = 3×5
300 122 -114 -228 -181
-291 -198 -105 -30 55
87 136 101 234 175
Результат, C, содержит пять независимых векторных произведений между столбцами A и B. Например, C(:,1) равно векторному произведению A(:,1) с B(:,1).
Создайте два 3 3х3 многомерными массивами случайных целых чисел.
A = randi(10,3,3,3); B = randi(25,3,3,3);
Найдите векторное произведение A и B, обработка строк как векторы.
C = cross(A,B,2)
C =
C(:,:,1) =
-34 12 62
15 72 -109
-49 8 9
C(:,:,2) =
198 -164 -170
45 0 -18
-55 190 -116
C(:,:,3) =
-109 -45 131
1 -74 82
-6 101 -121
Результатом является набор векторов-строк. Например, C(1,:,1) равно векторному произведению A(1,:,1) с B(1,:,1).
Найдите векторное произведение A и B по третьему измерению (dim = 3).
D = cross(A,B,3)
D =
D(:,:,1) =
-14 179 -106
-56 -4 -75
2 -37 10
D(:,:,2) =
-37 -162 -37
50 -124 -78
1 63 118
D(:,:,3) =
62 -170 56
46 72 105
-2 -53 -160
Результатом является набор векторов, ориентированных в третьей размерности. Например, D(1,1,:) равно векторному произведению A(1,1,:) с B(1,1,:).
A,B — Входные массивыВходные массивы, заданные как числовые массивы.
Типы данных: single | double
Поддержка комплексного числа: Да
dim — Размерность, которая задает направление расчетаВеличина для работы, заданная как положительный целый скаляр. Размер размерности dim должен быть 3. Если никакое значение не задано, значением по умолчанию является первое измерение массива, размер которого равняется 3.
Рассмотрите два 2D входных массива, A и B:
cross(A,B,1) обрабатывает столбцы A и B как векторы и возвращает векторные произведения соответствующих столбцов.
cross(A,B,2) обрабатывает строки A и B как векторы и возвращает векторные произведения соответствующих строк.

cross возвращает ошибку если dim больше ndims(A).
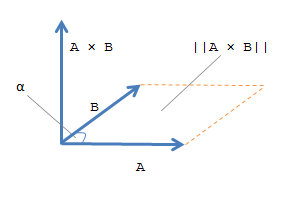
Векторное произведение между двумя 3-D векторами дает новый вектор, который перпендикулярен обоим.
Рассмотрите эти два вектора
В терминах определителя матрицы, включающего базисные векторы , , и , векторное произведение A и B
Геометрически, перпендикулярно и A и B. Величина векторного произведения, , равно области параллелограмма, сформированного с помощью A и B как стороны. Эта область связана с величинами A и B, а также угла между векторами
Таким образом, если A и B параллельны, то векторное произведение является нулем.
Указания и ограничения по применению:
Если предоставлено, dim должна быть константа.
Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.
Указания и ограничения по применению:
Если предоставлено, dim должна быть константа.
Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.
Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.