1D интерполяция данных (поиск по таблице)
vq = interp1(x,v,xq)x содержит точки выборки и v содержит соответствующие значения, v (x). Векторный xq содержит координаты точек запроса.
Если у вас есть несколько наборов данных, которые производятся в тех же координатах точки, то можно передать v как массив. Каждый столбец массива v содержит различный набор 1D демонстрационных значений.
vq = interp1(x,v,xq,method,extrapolation)x. Установите extrapolation к 'extrap' когда это необходимо, использовать method алгоритм для экстраполяции. В качестве альтернативы можно задать скалярное значение, в этом случае, interp1 возвращает то значение для всех точек вне области x.
vq = interp1(v,xq)1 к n, где n зависит от формы v:
Когда v является вектором, точками по умолчанию является 1:length(v).
Когда v является массивом, точками по умолчанию является 1:size(v,1).
Используйте этот синтаксис, когда вы не будете обеспокоены абсолютными расстояниями между точками.
vq = interp1(v,xq,method,extrapolation)
pp = interp1(x,v,method,'pp')method алгоритм.
Этот синтаксис не рекомендуется. Используйте griddedInterpolant вместо этого.
Задайте точки выборки, x, и соответствующие демонстрационные значения, v.
x = 0:pi/4:2*pi; v = sin(x);
Задайте точки запроса, чтобы быть более прекрасной выборкой в области значений x.
xq = 0:pi/16:2*pi;
Интерполируйте функцию в точках запроса и постройте результат.
figure vq1 = interp1(x,v,xq); plot(x,v,'o',xq,vq1,':.'); xlim([0 2*pi]); title('(Default) Linear Interpolation');

Теперь оцените v в тех же точках с помощью 'spline' метод.
figure vq2 = interp1(x,v,xq,'spline'); plot(x,v,'o',xq,vq2,':.'); xlim([0 2*pi]); title('Spline Interpolation');

Задайте набор значений функции.
v = [0 1.41 2 1.41 0 -1.41 -2 -1.41 0];
Задайте набор точек запроса, которые падают между точками по умолчанию, 1:9. В этом случае точками по умолчанию является 1:9 потому что v содержит 9 значения.
xq = 1.5:8.5;
Оцените v в xq.
vq = interp1(v,xq);
Постройте результат.
figure plot((1:9),v,'o',xq,vq,'*'); legend('v','vq');

Задайте набор точек выборки.
x = 1:10;
Задайте значения функции, , в точках выборки.
v = (5*x)+(x.^2*1i);
Задайте точки запроса, чтобы быть более прекрасной выборкой в области значений x.
xq = 1:0.25:10;
Интерполируйте v в точках запроса.
vq = interp1(x,v,xq);
Постройте действительную часть результата красного цвета и мнимой части синего цвета.
figure plot(x,real(v),'*r',xq,real(vq),'-r'); hold on plot(x,imag(v),'*b',xq,imag(vq),'-b');

Интерполируйте точки данных, к которым добавляют метку времени.
Рассмотрите набор данных, содержащий температурные показания, которые измеряются каждые четыре часа. Составьте таблицу с ценностью одного дня данных и отобразите данные на графике.
x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))'; x.Format = 'MMM dd, HH:mm'; T = [31 25 24 41 43 33 31]'; WeatherData = table(x,T,'VariableNames',{'Time','Temperature'})
WeatherData=7×2 table
Time Temperature
_____________ ___________
Jan 01, 00:00 31
Jan 01, 04:00 25
Jan 01, 08:00 24
Jan 01, 12:00 41
Jan 01, 16:00 43
Jan 01, 20:00 33
Jan 02, 00:00 31
plot(WeatherData.Time, WeatherData.Temperature, 'o')
Интерполируйте набор данных, чтобы предсказать температуру, читающую в течение каждой минуты дня. Поскольку данные являются периодическими, используйте 'spline' метод интерполяции.
xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';
V = interp1(WeatherData.Time, WeatherData.Temperature, xq, 'spline');Постройте интерполированные точки.
hold on plot(xq,V,'r')

Задайте точки выборки, x, и соответствующие демонстрационные значения, v.
x = [1 2 3 4 5]; v = [12 16 31 10 6];
Задайте точки запроса, xq, это расширяет вне области x.
xq = [0 0.5 1.5 5.5 6];
Оцените v в xq использование 'pchip' метод.
vq1 = interp1(x,v,xq,'pchip')vq1 = 1×5
19.3684 13.6316 13.2105 7.4800 12.5600
Затем оцените v в xq использование 'linear' метод.
vq2 = interp1(x,v,xq,'linear')vq2 = 1×5
NaN NaN 14 NaN NaN
Теперь используйте 'linear' метод с 'extrap' опция.
vq3 = interp1(x,v,xq,'linear','extrap')
vq3 = 1×5
8 10 14 4 2
'pchip' экстраполирует по умолчанию, но 'linear' не делает.
Задайте точки выборки, x, и соответствующие демонстрационные значения, v.
x = [-3 -2 -1 0 1 2 3]; v = 3*x.^2;
Задайте точки запроса, xq, это расширяет вне области x.
xq = [-4 -2.5 -0.5 0.5 2.5 4];
Теперь оцените v в xq использование 'pchip' метод и присвоение любые значения вне области x к значению, 27.
vq = interp1(x,v,xq,'pchip',27)vq = 1×6
27.0000 18.6562 0.9375 0.9375 18.6562 27.0000
Задайте точки выборки.
x = (-5:5)';
Демонстрационные три различных параболических функции в точках заданы в x.
v1 = x.^2; v2 = 2*x.^2 + 2; v3 = 3*x.^2 + 4;
Создайте матричный v, чьи столбцы являются векторами, v1, v2, и v3.
v = [v1 v2 v3];
Задайте набор точек запроса, xq, быть более прекрасной выборкой в области значений x.
xq = -5:0.1:5;
Выполните все три функции в xq и постройте результаты.
vq = interp1(x,v,xq,'pchip'); figure plot(x,v,'o',xq,vq); h = gca; h.XTick = -5:5;

Круги в графике представляют v, и сплошные линии представляют vq.
x 'SamplePoints' Точки выборки, заданные как строка или вектор-столбец вещественных чисел. Значения в x должно быть отличным. Длина x должен соответствовать одному из следующих требований:
Если v вектор, затем length(x) должен равняться length(v).
Если v массив, затем length(x) должен равняться size(v,1).
Пример: [1 2 3 4 5 6 7 8 9 10]
Пример: 1:10
Пример: [3 7 11 15 19 23 27 31]'
Типы данных: single | double | duration | datetime
v — Демонстрационные значенияДемонстрационные значения, заданные как вектор, матрица или массив вещественных или комплексных чисел. Если v матрица или массив, затем каждый столбец содержит отдельный набор 1D значений.
Если v содержит комплексные числа, затем interp1 интерполирует действительные и мнимые части отдельно.
Пример: rand(1,10)
Пример: rand(10,1)
Пример: rand(10,3)
Типы данных: single | double | duration | datetime
Поддержка комплексного числа: Да
xq — Точки запросаТочки запроса, заданные как скаляр, вектор, матрица или массив вещественных чисел.
Пример 5
Пример: 1:0.05:10
Пример: (1:0.05:10)'
Пример: [0 1 2 7.5 10]
Типы данных: single | double | duration | datetime
method метод интерполяции'linear' (значение по умолчанию) | 'nearest' | 'next' | 'previous' | 'pchip' | 'cubic' | 'v5cubic' | 'makima' | 'spline'Метод интерполяции, заданный как одна из опций в этой таблице.
|
Метод |
Описание |
Непрерывность |
Комментарии |
|---|---|---|---|
|
|
Линейная интерполяция. Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. Это - метод интерполяции по умолчанию. |
C0 |
|
|
|
Самая близкая соседняя интерполяция. Интерполированное значение в точке запроса является значением в самом близком демонстрационном узле решетки. |
Прерывистый |
|
|
|
Следующая соседняя интерполяция. Интерполированное значение в точке запроса является значением в следующем демонстрационном узле решетки. |
Прерывистый |
|
|
|
Предыдущая соседняя интерполяция. Интерполированное значение в точке запроса является значением в предыдущем демонстрационном узле решетки. |
Прерывистый |
|
|
|
Сохраняющая форму кусочная кубичная интерполяция. Интерполированное значение в точке запроса основано на сохраняющей форму кусочной кубичной интерполяции значений в соседних узлах решетки. |
C1 |
|
ПримечаниеПоведение
|
То же самое как |
C1 |
Этот метод в настоящее время возвращает тот же результат как |
|
|
Кубическая свертка используется в MATLAB® 5. |
C1 |
Точки должны быть расположены равными интервалами. |
|
|
Модифицированный Акима кубическая интерполяция Эрмита. Интерполированное значение в точке запроса основано на кусочно-линейной функции полиномов со степенью самое большее три. Формула Акима изменяется, чтобы избежать перерегулирований. |
C1 |
|
|
|
Интерполяция сплайна с помощью граничных условий не-узла. Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. |
C2 |
|
extrapolation — Стратегия экстраполяции'extrap' | скалярное значениеСтратегия экстраполяции, заданная как 'extrap' или действительное скалярное значение.
Задайте 'extrap' когда это необходимо, interp1 чтобы оценить точки вне области с помощью того же метода, это использует в интерполяции.
Задайте скалярное значение, когда это необходимо, interp1 возвращать определенное постоянное значение для точек вне области.
Поведение по умолчанию зависит от входных параметров:
Если вы задаете 'pchip'сплайн, или 'makima' методы интерполяции, затем поведением по умолчанию является 'extrap'.
Все другие методы интерполяции возвращают NaN по умолчанию для точек запроса вне области.
Пример: 'extrap'
Пример 5
Типы данных: char | string | single | double
vq — Интерполированные значенияИнтерполированные значения, возвращенные как скаляр, вектор, матрица или массив. Размер vq зависит от формы v и xq.
| Форма v | Форма xq | Размер Vq | Пример |
|---|---|---|---|
| Вектор | Вектор | size(xq) | Если size(v) = [1 100]и size(xq) = [1 500], затем size(vq) = [1 500]. |
| Вектор | Матрица или массив N-D | size(xq) | Если size(v) = [1 100]и size(xq) = [50 30], затем size(vq) = [50 30]. |
| Матрица или массив N-D | Вектор | [length(xq) size(v,2),...,size(v,n)] | Если size(v) = [100 3]и size(xq) = [1 500], затем size(vq) = [500 3]. |
| Матрица или массив N-D | Матрица или массив N-D | [size(xq,1),...,size(xq,n),... size(v,2),...,size(v,m)] | Если size(v) = [4 5 6]и size(xq) = [2 3 7], затем size(vq) = [2 3 7 5 6]. |
pp — Кусочный полиномКусочный полином, возвращенный как структура, которую можно передать ppval функция для оценки.
Алгоритм Акима для одномерной интерполяции, описанной в [1] и [2], выполняет кубичную интерполяцию, чтобы произвести кусочные полиномы с непрерывными производными первого порядка (C1). Алгоритм сохраняет наклон и избегает волнистостей в плоских областях. Плоская область происходит каждый раз, когда существует три или больше последовательных коллинеарных точки, которые алгоритм соединяет прямой линией. Чтобы гарантировать, что область между двумя точками данных является плоской, вставьте дополнительную точку данных между теми двумя точками.
Когда две плоских области с различными наклонами встречаются, модификация, сделанная к исходному алгоритму Акима, дает больше веса стороне, где наклон ближе к нулю. Эта модификация уделяет первостепенное значение стороне, которая ближе к горизонтали, которая более интуитивна и избегает перерегулирования. (Исходный алгоритм Акима дает равные веса точкам с обеих сторон, таким образом равномерно деля волнистость.)
Алгоритм сплайна, с другой стороны, выполняет кубичную интерполяцию, чтобы произвести кусочные полиномы с непрерывными производными второго порядка (C2). Результат сопоставим с регулярной полиномиальной интерполяцией, но менее восприимчив к тяжелому колебанию между точками данных для высоких степеней. Однако, этот метод может быть восприимчив к перерегулированиям и колебаниям между точками данных.
По сравнению с алгоритмом сплайна алгоритм Акима производит меньше волнистостей и лучше подходит для соглашения с быстрыми изменениями между плоскими областями. Это различие проиллюстрировано ниже использования тестовых данных, который соединяет несколько плоских областей.
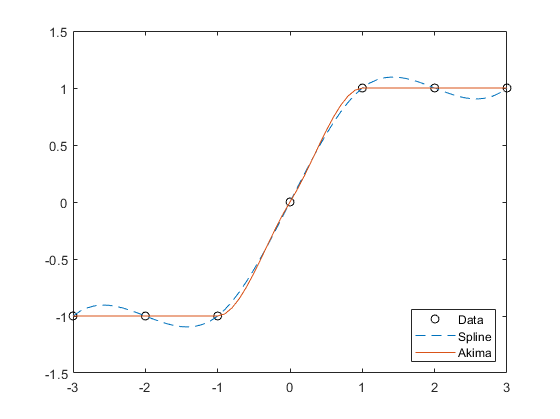
[1] Акима, Хироши. "Новый метод интерполяции и плавной кривой, соответствующей на основе локальных процедур". Журнал ACM (JACM), 17.4, 1970, стр 589-602.
[2] Акима, Хироши. "Метод двумерной интерполяции и сглаженной поверхности, соответствующей на основе локальных процедур". Коммуникации ACM, 17.1, 1974, стр 18-20.
Указания и ограничения по применению:
Генерация кода не поддерживает 'cubic' или 'makima' методы интерполяции.
Входной параметр x (точки выборки) должны строго увеличиваться или строго уменьшаться. Индексы не переупорядочиваются.
Если входной параметр v (демонстрационные значения), вектор переменной длины (1 : или :- 1), затем форма выхода vq совпадает с формой в MATLAB.
Если входной параметр v переменный размер, не вектор переменной длины и становится вектором-строкой во время выполнения, затем ошибка происходит.
Если входной параметр xq (точки запроса) являются переменным размером, не являются вектором переменной длины и становятся строкой или вектор-столбцом во время выполнения, затем ошибка происходит.
Указания и ограничения по применению:
x должен быть конечный, увеличивающийся вектор, не повторяя элементы. x должно быть двойным или одним.
v должен быть массив типа double или один. Размер первой неодноэлементной размерности v должен совпасть с длиной xV может быть комплексным.
xq должен быть массив типа double или один.
method должен быть 'linear'самый близкий, 'v5cubic', или 'spline'.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.