Ориентация от показаний магнитометра и акселерометра
orientation = ecompass(accelerometerReading,magnetometerReading)quaternion это может вращать количества от родительского элемента (NED) система координат дочернему элементу (датчик) система координат.
orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat)quaternion или матрица вращения.
orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat,'ReferenceFrame',RF)RF из orientation вывод . Задайте RF как 'NED' (Северо-восток вниз) или 'ENU' (Восточный Север). Значением по умолчанию является 'NED'.
Используйте известную силу магнитного поля, и соответствующее ускорение устройства указало истинный север в Бостоне, чтобы определить магнитный наклон Бостона.
Задайте известное ускорение и силу магнитного поля в Бостоне.
magneticFieldStrength = [19.535 -5.109 47.930]; properAcceleration = [0 0 9.8];
Передайте силу магнитного поля и ускорение к ecompass функция. ecompass функция возвращает оператор вращения кватерниона. Преобразуйте кватернион в Углы Эйлера в градусах.
q = ecompass(properAcceleration,magneticFieldStrength); e = eulerd(q,'ZYX','frame');
Угол, e, представляет угол между истинным северным и магнитным севером в Бостоне. Условно, магнитный наклон отрицателен, когда магнитный север к западу от истинного севера. Инвертируйте угол, чтобы определить магнитный наклон.
magneticDeclinationOfBoston = -e(1)
magneticDeclinationOfBoston = -14.6563
ecompass функционируйте магнитометр предохранителей и данные об акселерометре, чтобы возвратить кватернион, который, когда используется в операторе вращения кватерниона, может вращать количества от родительского элемента (NED) система координат к дочерней системе координат. ecompass функция может также возвратить матрицы вращения, которые выполняют эквивалентные вращения как оператор кватерниона.
Задайте вращение, которое может взять родительскую систему координат, указывающую на магнитный север к дочерней системе координат, указывающей на географический север. Задайте вращение и как кватернион и как матрицу вращения. Затем преобразуйте кватернион и матрицу вращения к Углам Эйлера в градусах для сравнения.
Задайте силу магнитного поля в микротесла в Бостоне, MA, когда указано истинный север.
m = [19.535 -5.109 47.930]; a = [0 0 9.8];
Определите кватернион и матрицу вращения, которая способна к вращению системы координат с магнитного севера на истинный север. Отобразите результаты для сравнения.
q = ecompass(a,m); quaterionEulerAngles = eulerd(q,'ZYX','frame')
quaterionEulerAngles = 1×3
14.6563 0 0
r = ecompass(a,m,'rotmat');
theta = -asin(r(1,3));
psi = atan2(r(2,3)/cos(theta),r(3,3)/cos(theta));
rho = atan2(r(1,2)/cos(theta),r(1,1)/cos(theta));
rotmatEulerAngles = rad2deg([rho,theta,psi])rotmatEulerAngles = 1×3
14.6563 0 0
Используйте ecompass определить вектор силы тяжести на основе данных из вращения IMU.
Загрузите данные об инерционном модуле измерения (IMU).
load 'rpy_9axis.mat' sensorData Fs
Определите ориентацию корпуса датчика относительно локальной системы координат NED в зависимости от времени.
orientation = ecompass(sensorData.Acceleration,sensorData.MagneticField);
Чтобы оценить вектор силы тяжести, сначала вращайте показания акселерометра от системы координат тела датчика до системы координат NED с помощью orientation вектор кватерниона.
gravityVectors = rotatepoint(orientation,sensorData.Acceleration);
Определите вектор силы тяжести как в среднем восстановленные векторы силы тяжести в зависимости от времени.
gravityVectorEstimate = mean(gravityVectors,1)
gravityVectorEstimate = 1×3
0.0000 -0.0000 10.2102
Плавьте смоделированный акселерометр и данные о гироскопе, чтобы отследить вращающуюся платформу с помощью и идеализированных и реалистических данных.
Сгенерируйте траекторию основной истины
Опишите ориентацию основной истины платформы в зависимости от времени. Используйте kinematicTrajectory Система object™, чтобы создать траекторию для платформы, которая не имеет никакого перевода и вращений о его оси z.
duration = 12;
fs = 100;
numSamples = fs*duration;
accelerationBody = zeros(numSamples,3);
angularVelocityBody = zeros(numSamples,3);
zAxisAngularVelocity = [linspace(0,4*pi,4*fs),4*pi*ones(1,4*fs),linspace(4*pi,0,4*fs)]';
angularVelocityBody(:,3) = zAxisAngularVelocity;
trajectory = kinematicTrajectory('SampleRate',fs);
[~,orientationNED,~,accelerationNED,angularVelocityNED] = trajectory(accelerationBody,angularVelocityBody);Модель, получающая данные IMU
Используйте imuSensor Системный объект, чтобы подражать данным получил от IMU, который содержит идеальный магнитометр и идеальный акселерометр.
IMU = imuSensor('accel-mag','SampleRate',fs); [accelerometerData,magnetometerData] = IMU(accelerationNED, ... angularVelocityNED, ... orientationNED);
Объедините данные IMU, чтобы оценить ориентацию
Передайте данные об акселерометре и данные о магнитометре к ecompass функционируйте, чтобы оценивать ориентацию в зависимости от времени. Преобразуйте ориентацию в Углы Эйлера в градусах и постройте результат.
orientation = ecompass(accelerometerData,magnetometerData); orientationEuler = eulerd(orientation,'ZYX','frame'); timeVector = (0:numSamples-1).'/fs; figure(1) plot(timeVector,orientationEuler) legend('z-axis','y-axis','x-axis') xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation from Ideal IMU')
Повторите эксперимент с реалистической моделью датчика IMU
Измените параметры IMU Системный объект, чтобы аппроксимировать реалистические данные о датчике IMU. Сбросьте IMU и затем вызовите его с тем же ускорением основной истины, скоростью вращения и ориентацией. Используйте ecompass объединять данные IMU и строить результаты.
IMU.Accelerometer = accelparams( ... 'MeasurementRange',20, ... 'Resolution',0.0006, ... 'ConstantBias',0.5, ... 'AxesMisalignment',2, ... 'NoiseDensity',0.004, ... 'BiasInstability',0.5); IMU.Magnetometer = magparams( ... 'MeasurementRange',200, ... 'Resolution',0.01); reset(IMU) [accelerometerData,magnetometerData] = IMU(accelerationNED,angularVelocityNED,orientationNED); orientation = ecompass(accelerometerData,magnetometerData); orientationEuler = eulerd(orientation,'ZYX','frame'); figure(2) plot(timeVector,orientationEuler) legend('z-axis','y-axis','x-axis') xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation from Realistic IMU')
ecompass функция возвращает кватернион или матрицу вращения, которая может вращать количества от родительского элемента (NED, например) система координат дочернему элементу (датчик) система координат. Для обоих выходных форматов ориентации оператор вращения определяется путем вычисления матрицы вращения.
Матрица вращения сначала вычисляется с посредником:
и затем нормированный по столбцам. a и m является accelerometerReading введите и magnetometerReading введите, соответственно.
Чтобы изучить матричное вычисление вращения, рассмотрите произвольную точку на Земле и ее соответствующей локальной системе координат NED. Примите систему координат тела датчика, [x, y, z], с тем же источником.
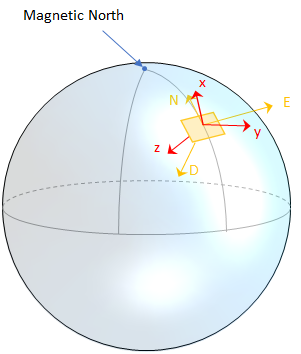
Вспомните, что ориентация корпуса датчика задана как оператор вращения (матрица вращения или кватернион) требуемый вращать количество от родительского элемента (NED) система координат дочернему элементу (корпус датчика) система координат:
где
R является 3х3 матрицей вращения, которая может быть интерпретирована как ориентация дочерней системы координат.
Родительский элемент p является вектором 3 на 1 в родительской системе координат.
Дочерний элемент p является вектором 3 на 1 в дочерней системе координат.
Для устойчивого корпуса датчика акселерометр возвращает ускорение из-за силы тяжести. Если корпус датчика отлично выравнивается с системой координат NED, все ускорение из-за силы тяжести приезжает z - ось и чтения акселерометра [0 0 1]. Считайте матрицу вращения требуемой вращать количество от системы координат NED до количества, обозначенного акселерометром.
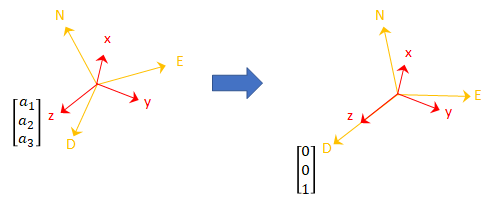
Третий столбец матрицы вращения соответствует чтению акселерометра:
Магнитометр, читая точки к магнитному северу и находится в N-D плоскость. Снова, считайте систему координат тела датчика выровненной с системой координат NED.
По определению E - ось перпендикулярна N-D плоскость, поэтому N ⨯ D = E, в рамках некоторого амплитудного масштабирования. Если система координат тела датчика выравнивается с NED, и ускоряющий вектор от акселерометра и вектор магнитного поля от магнитометра лежат в N-D плоскость. Поэтому m ⨯ a = y, снова с некоторым амплитудным масштабированием.
Считайте матрицу вращения требуемой вращать NED к дочерней системе координат, [x y z].
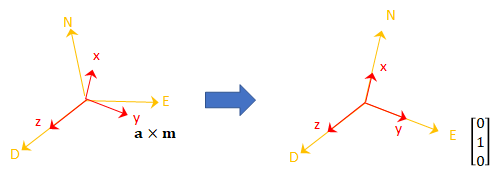
Второй столбец матрицы вращения соответствует векторному произведению чтения акселерометра и чтения магнитометра:
По определению матрицы вращения, столбец 1 является векторным произведением столбцов 2 и 3:
Наконец, матрица вращения нормирована по столбцам:
ecompass алгоритм использует магнитный север, не истинный север, для системы координат NED.
[1] Fusion датчика с открытым исходным кодом. https://github.com/memsindustrygroup/Open-Source-Sensor-Fusion/tree/master/docs