Минимизация с шаблоном разреженности градиента и гессиана

В этом примере показано, как решить нелинейную задачу минимизации с трехдиагональной матрицей Гессиана, аппроксимированной разреженными конечными разностями вместо явного расчета.

Проблема состоит в том, чтобы найти, что x минимизирует

$f (x) = \sum_{i = 1}^{n - 1} ({(x_{i}^{2})}^{(x_{i + 1}^{2} + 1)} + {(x_{i + 1}^{2})}^{(x_{i}^{2} + 1)}),$

где n = 1000.

Использовать trust-region метод в fminunc, необходимо вычислить градиент в fun; это не является дополнительным как в quasi-newton метод.

brownfg файл вычисляет целевую функцию и градиент.

Шаг 1: Запишите файл brownfg.m, который вычисляет целевую функцию и градиент цели.

Этот файл функции поставляется с вашим программным обеспечением.

function [f,g] = brownfg(x)
% BROWNFG Nonlinear minimization test problem
% 
% Evaluate the function
n=length(x); y=zeros(n,1);
i=1:(n-1);
y(i)=(x(i).^2).^(x(i+1).^2+1) + ...
        (x(i+1).^2).^(x(i).^2+1);
  f=sum(y);
% Evaluate the gradient if nargout > 1
  if nargout > 1
     i=1:(n-1); g = zeros(n,1);
     g(i) = 2*(x(i+1).^2+1).*x(i).* ...
              ((x(i).^2).^(x(i+1).^2))+ ...
              2*x(i).*((x(i+1).^2).^(x(i).^2+1)).* ...
              log(x(i+1).^2);
     g(i+1) = g(i+1) + ...
              2*x(i+1).*((x(i).^2).^(x(i+1).^2+1)).* ...
              log(x(i).^2) + ...
              2*(x(i).^2+1).*x(i+1).* ...
              ((x(i+1).^2).^(x(i).^2));
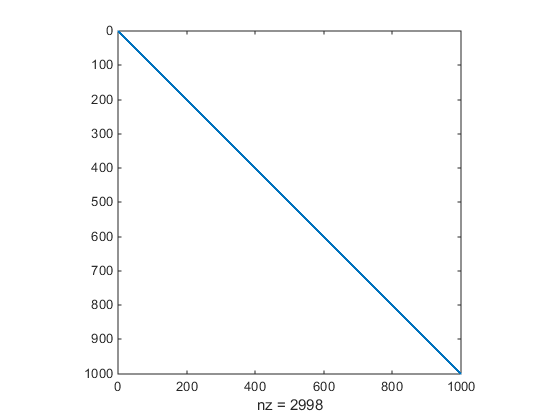
  end

Чтобы позволить эффективный расчет разреженного приближения конечной разности матрицы Гессиана H (x), структура разреженности H должна быть предопределена. В этом случае примите эту структуру, Hstr, разреженная матрица, доступно в файле brownhstr.mat. Используя spy команда вы видите тот Hstr действительно разреженно (только 2 998 ненулей). Используйте optimoptions установить HessPattern опция к Hstr. Когда проблема, столь большая, как это имеет очевидную структуру разреженности, не устанавливая HessPattern опция требует огромной суммы ненужной памяти и расчета потому что fminunc попытки использовать конечное дифференцирование на полной матрице Гессиана одного миллиона ненулевых записей.

Необходимо также установить SpecifyObjectiveGradient опция к true использование optimoptions, поскольку градиент вычисляется в brownfg.m. Затем выполните fminunc как показано на Шаге 2.

Шаг 2: Вызовите нелинейную стандартную программу минимизации с начальной точкой xstart.

fun = @brownfg;
load brownhstr % Get Hstr, structure of the Hessian
spy(Hstr) % View the sparsity structure of Hstr

n = 1000;
xstart = -ones(n,1); 
xstart(2:2:n,1) = 1;
options = optimoptions(@fminunc,'Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true,'HessPattern',Hstr);
[x,fval,exitflag,output] = fminunc(fun,xstart,options);

Эта задача с 1000 переменными решена в семи итерациях и семи итерациях метода сопряженных градиентов с положительным exitflag указание на сходимость. Итоговое значение функции и мера оптимальности в решении x оба близко к нулю (для fminunc, оптимальность первого порядка является нормой по бесконечности градиента функции, которая является нулем в локальном минимуме):

exitflag,fval,output.firstorderopt

exitflag =

     1


fval =

   7.4738e-17


ans =

   7.9822e-10

Документация