Symbolic Math Toolbox вычисляет градиенты и гессианы

Если у вас есть лицензия Symbolic Math Toolbox™, можно легко вычислить аналитические градиенты и Гессианы для ограничительных функций и цели. Существует две соответствующих функции Symbolic Math Toolbox:

jacobian генерирует градиент скалярной функции и генерирует матрицу частных производных вектор-функции. Так, например, можно получить матрицу Гессиана, вторые производные целевой функции, путем применения jacobian к градиенту. Часть этого примера показывает, как использовать jacobian сгенерировать символьные градиенты и Гессианы ограничительных функций и цели.
matlabFunction генерирует или анонимную функцию или файл, который вычисляет значения символьного выражения. В этом примере показано, как использовать matlabFunction сгенерировать файлы, которые оценивают цель и ограничительную функцию и их производные в произвольных точках.

Рассмотрите проблему электростатики размещения 10 электронов в органе по проведению. Электроны расположат себя, чтобы минимизировать их общую потенциальную энергию согласно ограничению лжи в теле. Известно, что все электроны будут на контуре тела как минимум. Электроны неразличимы, таким образом, нет никакого уникального минимума для этой проблемы (переставляющий электроны в одном решении, дает другое допустимое решение). Этот пример был вдохновлен Доланом, Море и Мансоном [58].

Этим примером является орган по проведению, заданный следующими неравенствами:

z \leq - | x | - | y |

(1)

x^{2} + y^{2} + {(z + 1)}^{2} \leq 1.

(2)

Это тело похоже на пирамиду на сфере.

Код для генерации фигуры

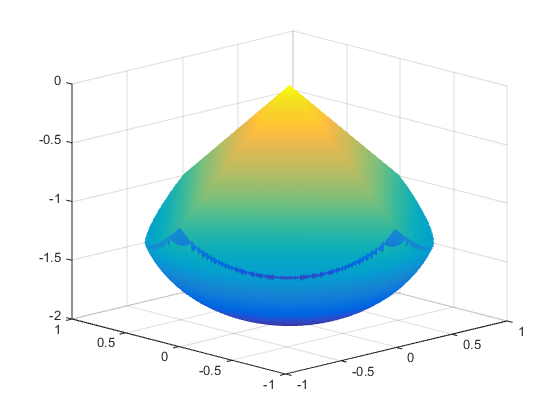
Существует небольшой разрыв между верхними и более низкими поверхностями фигуры. Это - артефакт общей стандартной программы графического вывода, используемой, чтобы создать фигуру. Эта стандартная программа стирает любую прямоугольную закрашенную фигуру на одной поверхности, которая касается другой поверхности.

Синтаксис и структуры двух наборов функций тулбокса отличаются. В частности, символьные переменные являются действительными или комплексными скалярами, но функции Optimization Toolbox™ передают аргументы вектора. Таким образом, существует несколько шагов, чтобы взять, чтобы сгенерировать символически целевую функцию, ограничения и все их необходимые производные, в форме, подходящей для алгоритма внутренней точки fmincon:

Чтобы видеть КПД в использовании градиентов и Гессианов, смотрите, Выдерживают сравнение с Оптимизацией Без Градиентов и Гессианов. Для подхода, основанного на проблеме к этой проблеме, не используя производную информацию, смотрите Ограниченную Электростатическую Нелинейную Оптимизацию, Основанную на проблеме.

Создайте переменные

Сгенерируйте символьный векторный x как 30 1 вектор, состоявший из действительных символьных переменных xiji между 1 и 10, и j между 1 и 3. Эти переменные представляют три координаты электронного i: xi1 соответствует координате x, xi2 соответствует координате y и xi3 соответствует координате z.

x = cell(3, 10);
for i = 1:10
    for j = 1:3
        x{j,i} = sprintf('x%d%d',i,j);
    end
end
x = x(:); % now x is a 30-by-1 vector
x = sym(x, 'real');

Векторный x :

Включайте линейные ограничения

Напишите линейные ограничения в уравнении 1,

z ≤ – |x | – |y |,

как набор четырех линейных неравенств для каждого электрона:

xi3 – xi1 – xi2 ≤ 0
xi3 – xi1 + xi2 ≤ 0
xi3 + xi1 – xi2 ≤ 0
xi3 + xi1 + xi2 ≤ 0

Поэтому существует в общей сложности 40 линейных неравенств для этой проблемы.

Запишите неравенства структурированным способом:

B = [1,1,1;-1,1,1;1,-1,1;-1,-1,1];

A = zeros(40,30);
for i=1:10
    A(4*i-3:4*i,3*i-2:3*i) = B;
end

b = zeros(40,1);

Вы видите тот A*x ≤ b представляет неравенства:

A*x
 
ans = 
    x11 + x12 + x13
    x12 - x11 + x13
    x11 - x12 + x13
    x13 - x12 - x11
    x21 + x22 + x23
    x22 - x21 + x23
    x21 - x22 + x23
    x23 - x22 - x21
    x31 + x32 + x33
    x32 - x31 + x33
    x31 - x32 + x33
    x33 - x32 - x31
    x41 + x42 + x43
    x42 - x41 + x43
    x41 - x42 + x43
    x43 - x42 - x41
    x51 + x52 + x53
    x52 - x51 + x53
    x51 - x52 + x53
    x53 - x52 - x51
    x61 + x62 + x63
    x62 - x61 + x63
    x61 - x62 + x63
    x63 - x62 - x61
    x71 + x72 + x73
    x72 - x71 + x73
    x71 - x72 + x73
    x73 - x72 - x71
    x81 + x82 + x83
    x82 - x81 + x83
    x81 - x82 + x83
    x83 - x82 - x81
    x91 + x92 + x93
    x92 - x91 + x93
    x91 - x92 + x93
    x93 - x92 - x91
 x101 + x102 + x103
 x102 - x101 + x103
 x101 - x102 + x103
 x103 - x102 - x101

Создайте нелинейные ограничения, их градиенты и гессианы

Нелинейные ограничения в уравнении 2,

$x^{2} + y^{2} + {(z + 1)}^{2} \leq 1,$

также структурированы. Сгенерируйте ограничения, их градиенты и Гессианы можно следующим образом:

c = sym(zeros(1,10));
i = 1:10;
c = (x(3*i-2).^2 + x(3*i-1).^2 + (x(3*i)+1).^2 - 1).';

gradc = jacobian(c,x).'; % .' performs transpose

hessc = cell(1, 10);
for i = 1:10
    hessc{i} = jacobian(gradc(:,i),x);
end

Ограничительный вектор c вектор-строка и градиент c(i) представлен в iстолбец th матричного gradc. Это - правильная форма, как описано в Нелинейных Ограничениях.

Матрицы Гессиана, hessc{1}... hessc{10}, являются квадратными и симметричными. Лучше сохранить их в массиве ячеек, как сделан здесь, чем в отдельных переменных, таких как hessc1, ..., hesssc10.

Используйте .' синтаксис, чтобы транспонировать. ' синтаксис означает сопряженное транспонирование, которое имеет различные символьные производные.

Создайте целевую функцию, ее градиент и гессиан

Целевая функция, потенциальная энергия, является суммой инверсий расстояний между каждой электронной парой:

$энергия = \sum_{i < j} \frac{1}{| x_{i} - x_{j} |} .$

Расстояние является квадратным корнем из суммы квадратов различий в компонентах векторов.

Вычислите энергию, ее градиент и ее Гессиан можно следующим образом:

energy = sym(0);
for i = 1:3:25
    for j = i+3:3:28
        dist = x(i:i+2) - x(j:j+2);
        energy = energy + 1/sqrt(dist.'*dist);
    end
end

gradenergy = jacobian(energy,x).';

hessenergy = jacobian(gradenergy,x);

Создайте файл целевой функции

Целевая функция должна иметь два выходных параметров, energy и gradenergy. Поместите обе функции в один вектор при вызове matlabFunction сокращать количество подвыражений что matlabFunction генерирует, и возвратить градиент только когда функция вызова (fmincon в этом случае), запрашивает оба выходных параметров. Этот пример показывает размещение получившихся файлов в вашей текущей папке. Конечно, можно разместить их куда угодно, вам нравится, пока папка находится на пути MATLAB.

currdir = [pwd filesep]; % You may need to use currdir = pwd 
filename = [currdir,'demoenergy.m'];
matlabFunction(energy,gradenergy,'file',filename,'vars',{x});

Этот синтаксис вызывает matlabFunction возвратить energy как первый выход и gradenergy как второе. Это также берет одному входному вектору {x} вместо списка входных параметров x11..., x103.

Получившийся файл demoenergy.m содержит, частично, следующие линии или подобные единицы:

function [energy,gradenergy] = demoenergy(in1)
%DEMOENERGY
%   [ENERGY,GRADENERGY] = DEMOENERGY(IN1)
...
x101 = in1(28,:);
...
energy = 1./t140.^(1./2) + ...;
if nargout > 1
    ...
    gradenergy = [(t174.*(t185 - 2.*x11))./2 - ...];
end

Эта функция имеет правильную форму для целевой функции с градиентом; смотрите Пишущие Скалярные Целевые функции.

Создайте ограничительный файл функции

Сгенерируйте нелинейную ограничительную функцию и поместите ее в правильный формат.

filename = [currdir,'democonstr.m'];
matlabFunction(c,[],gradc,[],'file',filename,'vars',{x},...
    'outputs',{'c','ceq','gradc','gradceq'});

Получившийся файл democonstr.m содержит, частично, следующие линии или подобные единицы:

function [c,ceq,gradc,gradceq] = democonstr(in1)
%DEMOCONSTR
%    [C,CEQ,GRADC,GRADCEQ] = DEMOCONSTR(IN1)
...
x101 = in1(28,:);
...
c = [t417.^2 + ...];
if nargout > 1
    ceq = [];
end
if nargout > 2
    gradc = [2.*x11,...];
end
if nargout > 3
    gradceq = [];
end

Эта функция имеет правильную форму для ограничительной функции с градиентом; смотрите Нелинейные Ограничения.

Сгенерируйте файлы гессиана

Чтобы сгенерировать Гессиан функции Лагранжа для проблемы, сначала сгенерируйте файлы для энергетического Гессиана и для ограничительных Гессианов.

Гессиан целевой функции, hessenergy, очень большое символьное выражение, содержа более чем 150 000 символов, как оценка size(char(hessenergy)) показывает. Таким образом, требуется значительное количество времени, чтобы запустить matlabFunction(hessenergy).

Сгенерировать файл hessenergy.m, запустите следующие две линии:

filename = [currdir,'hessenergy.m'];
matlabFunction(hessenergy,'file',filename,'vars',{x});

В отличие от этого Гессианы ограничительных функций малы, и быстро вычислить:

for i = 1:10
    ii = num2str(i);
    thename = ['hessc',ii];
    filename = [currdir,thename,'.m'];
    matlabFunction(hessc{i},'file',filename,'vars',{x});
end

После генерации всех файлов для цели и ограничений, помещает их вместе с соответствующими множителями Лагранжа в файле hessfinal.m можно следующим образом:

function H = hessfinal(X,lambda)
%
% Call the function hessenergy to start
H = hessenergy(X);

% Add the Lagrange multipliers * the constraint Hessians
H = H + hessc1(X) * lambda.ineqnonlin(1);
H = H + hessc2(X) * lambda.ineqnonlin(2);
H = H + hessc3(X) * lambda.ineqnonlin(3);
H = H + hessc4(X) * lambda.ineqnonlin(4);
H = H + hessc5(X) * lambda.ineqnonlin(5);
H = H + hessc6(X) * lambda.ineqnonlin(6);
H = H + hessc7(X) * lambda.ineqnonlin(7);
H = H + hessc8(X) * lambda.ineqnonlin(8);
H = H + hessc9(X) * lambda.ineqnonlin(9);
H = H + hessc10(X) * lambda.ineqnonlin(10);

Запустите оптимизацию

Запустите оптимизацию с электронов, распределенных случайным образом на сфере радиуса 1/2 сосредоточенный в [0,0, –1]:

rng default % for reproducibility
Xinitial = randn(3,10); % columns are normal 3-D vectors
for j=1:10
    Xinitial(:,j) = Xinitial(:,j)/norm(Xinitial(:,j))/2;
    % this normalizes to a 1/2-sphere
end
Xinitial(3,:) = Xinitial(3,:) - 1; % center at [0,0,-1]
Xinitial = Xinitial(:); % Convert to a column vector

Установите опции использовать алгоритм внутренней точки и использовать градиенты и Гессиан:

options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true,'HessianFcn',@hessfinal,'Display','final');

Вызовите fmincon:

[xfinal fval exitflag output] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Решение берет 19 итераций и только 28 функциональных оценок:

xfinal,fval,exitflag,output.iterations,output.funcCount

xfinal =

   -0.0317
    0.0317
   -1.9990
    0.6356
   -0.6356
   -1.4381
    0.0000
   -0.0000
   -0.0000
    0.0000
   -1.0000
   -1.0000
    1.0000
   -0.0000
   -1.0000
   -1.0000
   -0.0000
   -1.0000
    0.6689
    0.6644
   -1.3333
   -0.6667
    0.6667
   -1.3333
    0.0000
    1.0000
   -1.0000
   -0.6644
   -0.6689
   -1.3333


fval =

   34.1365


exitflag =

     1


ans =

    19


ans =

    28

Даже при том, что исходные положения электронов были случайны, конечные положения почти симметричны:

Код для генерации фигуры

Сравните с оптимизацией без градиентов и гессианов

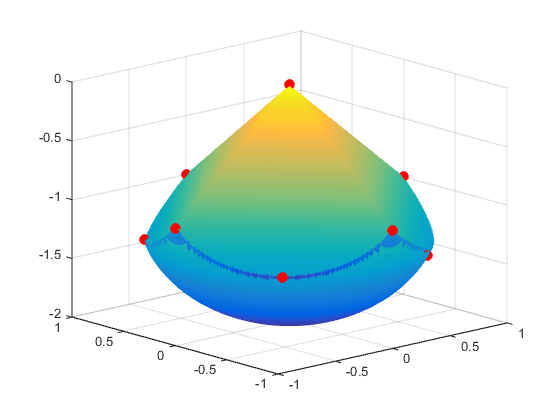
Использование градиентов и Гессианов делает оптимизацию запущенной быстрее и более точно. Чтобы соответствовать той же оптимизации, не используя градиента или информации о Гессиане, установите опции не использовать градиенты и Гессианы:

options = optimoptions(@fmincon,'Algorithm','interior-point',...
    'Display','final');
[xfinal2 fval2 exitflag2 output2] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Выход показывает тот fmincon найденный эквивалентным минимумом, но взял больше итераций и намного больше функциональных оценок, чтобы сделать так.

xfinal2,fval2,exitflag2,output2.iterations,output2.funcCount

xfinal2 =

    0.0000
    1.0000
   -1.0000
    0.6689
   -0.6644
   -1.3334
   -0.6644
    0.6689
   -1.3334
    0.0000
   -1.0000
   -1.0000
    0.6357
    0.6357
   -1.4380
   -0.0317
   -0.0317
   -1.9990
    1.0000
    0.0000
   -1.0000
   -1.0000
    0.0000
   -1.0000
    0.0000
    0.0000
   -0.0000
   -0.6667
   -0.6667
   -1.3334


fval2 =

   34.1365


exitflag2 =

     1


ans =

    75


ans =

    2372

В этом запуске количество функциональных оценок (в output2.funcCount) 2372 по сравнению с 28 (в output.funcCount) при использовании градиентов и Гессиана.

Очистите символьные переменные предположения

Символьные переменные в этом примере имеют предположение в символьной рабочей области механизма, что они действительны. Чтобы очистить это предположение от символьной рабочей области механизма, не достаточно удалить переменные. Очистите переменные предположения при помощи syms:

syms x

Проверьте, что предположения пусты.

assumptions(x)

ans =
 
Empty sym: 1-by-0

Документация