Постройте решение или поверхностную mesh для 3-D проблемы
pdeplot3D( строит решение в узловых местоположениях как цвета на поверхности 3-D геометрии, заданной в model,'ColorMapData',results.NodalSolution)model.
pdeplot3D( строит температуру в узловых местоположениях для 3-D тепловой аналитической модели.model,'ColorMapData',results.Temperature)
pdeplot3D(___, строит поверхностную mesh, данные в узловых местоположениях, или и mesh и данные, в зависимости от Name,Value)Name,Value парные аргументы. Используйте любые аргументы от предыдущих синтаксисов.
h = pdeplot3D(___)
Постройте решение для УЧП на поверхности геометрии. Во-первых, создайте модель PDE и импортируйте 3-D файл геометрии. Задайте граничные условия и коэффициенты. Поймайте в сети геометрию и решите задачу.
model = createpde; importGeometry(model,'Block.stl'); applyBoundaryCondition(model,'dirichlet','Face',[1:4],'u',0); specifyCoefficients(model,'m',0,'d',0,'c',1,'a',0,'f',2); generateMesh(model); results = solvepde(model)
results =
StationaryResults with properties:
NodalSolution: [12691x1 double]
XGradients: [12691x1 double]
YGradients: [12691x1 double]
ZGradients: [12691x1 double]
Mesh: [1x1 FEMesh]
Доступ к решению в узловых местоположениях.
u = results.NodalSolution;
Постройте решение u на поверхности геометрии.
pdeplot3D(model,'ColorMapData',u)
Решите 3-D установившуюся тепловую задачу.
Создайте тепловую модель для этой проблемы.
thermalmodel = createpde('thermal');Импортируйте и постройте геометрию блока.
importGeometry(thermalmodel,'Block.stl'); pdegplot(thermalmodel,'FaceLabel','on','FaceAlpha',0.5) axis equal
Присвойте свойства материала.
thermalProperties(thermalmodel,'ThermalConductivity',80);Примените постоянную температуру к левой стороне блока (стоят 1), и постоянная температура к правой стороне блока (стоят 3). Все другие поверхности изолируются по умолчанию.
thermalBC(thermalmodel,'Face',1,'Temperature',100); thermalBC(thermalmodel,'Face',3,'Temperature',300);
Поймайте в сети геометрию и решите задачу.
generateMesh(thermalmodel); thermalresults = solve(thermalmodel)
thermalresults =
SteadyStateThermalResults with properties:
Temperature: [12691x1 double]
XGradients: [12691x1 double]
YGradients: [12691x1 double]
ZGradients: [12691x1 double]
Mesh: [1x1 FEMesh]
Решатель находит температуры и градиенты температуры в узловых местоположениях. Чтобы получить доступ к этим значениям, используйте thermalresults.Temperature, thermalresults.XGradients, и так далее. Например, постройте температуры в узловых местоположениях.
pdeplot3D(thermalmodel,'ColorMapData',thermalresults.Temperature)
Для 3-D установившейся тепловой модели оцените поток тепла в узловых местоположениях и в точках, заданных xY, и z координаты.
Создайте тепловую модель для установившегося анализа.
thermalmodel = createpde('thermal');Создайте следующую 3-D геометрию и включайте ее в модель.
importGeometry(thermalmodel,'Block.stl'); pdegplot(thermalmodel,'FaceLabels','on','FaceAlpha',0.5) title('Copper block, cm') axis equal
Предположение, что это - медный блок, теплопроводность блока приблизительно .
thermalProperties(thermalmodel,'ThermalConductivity',4);Применяйтесь постоянная температура 373 K к левой стороне блока (столкнитесь 1), и постоянная температура 573 K к правой стороне блока (столкнитесь 3).
thermalBC(thermalmodel,'Face',1,'Temperature',373); thermalBC(thermalmodel,'Face',3,'Temperature',573);
Примените граничное условие потока тепла к нижней части блока.
thermalBC(thermalmodel,'Face',4,'HeatFlux',-20);
Поймайте в сети геометрию и решите задачу.
generateMesh(thermalmodel); thermalresults = solve(thermalmodel)
thermalresults =
SteadyStateThermalResults with properties:
Temperature: [12691x1 double]
XGradients: [12691x1 double]
YGradients: [12691x1 double]
ZGradients: [12691x1 double]
Mesh: [1x1 FEMesh]
Оцените поток тепла в узловых местоположениях.
[qx,qy,qz] = evaluateHeatFlux(thermalresults);
figure
pdeplot3D(thermalmodel,'FlowData',[qx qy qz])
Создайте сетку, заданную xY, и z координаты, и оценивают поток тепла к сетке.
[X,Y,Z] = meshgrid(1:26:100,1:6:20,1:11:50); [qx,qy,qz] = evaluateHeatFlux(thermalresults,X,Y,Z);
Измените qxqy , и qz векторы и график получившийся поток тепла.
qx = reshape(qx,size(X)); qy = reshape(qy,size(Y)); qz = reshape(qz,size(Z)); figure quiver3(X,Y,Z,qx,qy,qz)
В качестве альтернативы можно задать сетку при помощи матрицы точек запроса.
querypoints = [X(:) Y(:) Z(:)]'; [qx,qy,qz] = evaluateHeatFlux(thermalresults,querypoints); qx = reshape(qx,size(X)); qy = reshape(qy,size(Y)); qz = reshape(qz,size(Z)); figure quiver3(X,Y,Z,qx,qy,qz)
Создайте модель структурного анализа для 3-D проблемы.
structuralmodel = createpde('structural','static-solid');
Импортируйте геометрию и постройте ее.
importGeometry(structuralmodel,'SquareBeam.STL'); pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.5)
Задайте модуль Молодежи и отношение Пуассона.
structuralProperties(structuralmodel,'PoissonsRatio',0.3, ... 'YoungsModulus',210E3);
Укажите, что стоят 6, фиксированный контур.
structuralBC(structuralmodel,'Face',6,'Constraint','fixed');
Задайте поверхностную тягу для поверхности 5.
structuralBoundaryLoad(structuralmodel,'Face',5,'SurfaceTraction',[0;0;-2]);
Сгенерируйте mesh и решите задачу.
generateMesh(structuralmodel); structuralresults = solve(structuralmodel);
Постройте деформированную форму с напряжением фон Мизеса с помощью масштабного коэффициента по умолчанию. По умолчанию, pdeplot3D внутренне определяет масштабный коэффициент на основе размерностей геометрии и величины деформации.
figure pdeplot3D(structuralmodel,'ColorMapData',structuralresults.VonMisesStress, ... 'Deformation',structuralresults.Displacement)
Постройте те же результаты с масштабным коэффициентом 500.
figure pdeplot3D(structuralmodel,'ColorMapData',structuralresults.VonMisesStress, ... 'Deformation',structuralresults.Displacement, ... 'DeformationScaleFactor',500)
Постройте те же результаты без масштабирования.
figure
pdeplot3D(structuralmodel,'ColorMapData',structuralresults.VonMisesStress)
Оцените напряжение фон Мизеса в луче при гармоническом возбуждении.
Создайте переходную динамическую модель для 3-D проблемы.
structuralmodel = createpde('structural','transient-solid');
Создайте геометрию и включайте ее в модель. Постройте геометрию.
gm = multicuboid(0.06,0.005,0.01); structuralmodel.Geometry = gm; pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.5) view(50,20)
Задайте модуль Молодежи, отношение Пуассона и массовую плотность материала.
structuralProperties(structuralmodel,'YoungsModulus',210E9, ... 'PoissonsRatio',0.3, ... 'MassDensity',7800);
Зафиксируйте один конец луча.
structuralBC(structuralmodel,'Face',5,'Constraint','fixed');
Примените синусоидальное смещение вдоль направления Y на конце напротив фиксированного конца луча.
structuralBC(structuralmodel,'Face',3,'YDisplacement',1E-4,'Frequency',50);
Сгенерируйте mesh.
generateMesh(structuralmodel,'Hmax',0.01);Определите нулевое начальное перемещение и скорость.
structuralIC(structuralmodel,'Displacement',[0;0;0],'Velocity',[0;0;0]);
Решите модель.
tlist = 0:0.002:0.2; structuralresults = solve(structuralmodel,tlist);
Оцените напряжение фон Мизеса в луче.
vmStress = evaluateVonMisesStress(structuralresults);
Постройте напряжение фон Мизеса в течение прошлого такта.
figure pdeplot3D(structuralmodel,'ColorMapData',vmStress(:,end)) title('von Mises Stress in the Beam for the Last Time-Step')
Создайте модель PDE, включайте геометрию и сгенерируйте mesh.
model = createpde; importGeometry(model,'Tetrahedron.stl'); mesh = generateMesh(model,'Hmax',20,'GeometricOrder','linear');
Постройте поверхностную mesh.
pdeplot3D(model)
В качестве альтернативы можно построить mesh при помощи mesh как входной параметр.
pdeplot3D(mesh)
Другой подход должен использовать узлы и элементы mesh как входные параметры для pdeplot3D.
pdeplot3D(mesh.Nodes,mesh.Elements)
Отобразите метки узла на поверхности простой mesh.
pdeplot3D(model,'NodeLabels','on') view(101,12)
Отобразите метки элемента.
pdeplot3D(model,'ElementLabels','on') view(101,12)
model — Объект моделиPDEModel возразите | ThermalModel возразите | StructuralModel объектОбъект модели, заданный как PDEModel объект, ThermalModel объект или StructuralModel объект.
Пример: model = createpde(1)
Пример: thermalmodel = createpde('thermal','steadystate')
Пример: structuralmodel = createpde('structural','static-solid')
mesh — Объект ячейкиMesh свойство PDEModel возразите | выход generateMeshОбъект ячейки, заданный как Mesh свойство PDEModel возразите или как выход generateMesh.
Пример: model.Mesh
nodes — Узловые координатыУзловые координаты, заданные как 3 NumNodes матрицей. NumNodes является количеством узлов.
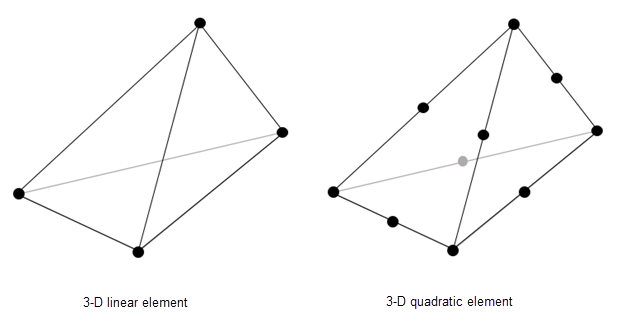
elements — Матрица смежности элемента в терминах идентификаторов узлаМатрица смежности элемента в терминах идентификаторов узла, заданных как 4 NumElements или 10 NumElements матрицей. Линейные сетки содержат только угловые узлы. Для линейных сеток матрица смежности имеет четыре узла на 3-D элемент. Квадратичные сетки содержат угловые узлы и узлы посреди каждого ребра элемента. Для квадратичных сеток матрица смежности имеет 10 узлов на 3-D элемент.
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
pdeplot3D(model,'NodeLabels','on')