Это содержимое характерно для программного обеспечения Simscape™ Multibody™ First Generation. Функции первого поколения намечают, чтобы быть удержанными от использования и нужно избежать.
Машины состоят из тел, которые имеют относительные степени свободы (число степеней свободы). Тела имеют положения, ориентации, массовые свойства и наборы систем координат Тела. Соединения представляют движения тел.
Геометрия машины состоит из своих статических функций тела прежде, чем запустить симуляцию: положения, ориентации и системы координат Тела.
Кинематика машины состоит из всех степеней свободы (число степеней свободы) всех тел: положения/ориентации и их производные в любой момент во время движения машины.
Полное описание движения машины включает не только свою кинематику, но также и спецификацию его наблюдателей, которые задают системы координат (RFs) и системы координат (CSS) для измерения движения машины.
Все векторы и тензоры, если не указано иное, представлены Декартовыми матрицами с три и девять, соответственно, пространственные компоненты, измеренные осями прямоугольной координаты.
Система координат наблюдателя является состоянием наблюдателя движения, которое должно быть измерено другими наблюдателями. Модель Simscape Multibody симулирует движение машины с помощью своей ньютоновой динамики, которая принимает его самую простую форму в наборе инерционного RFs, наборе всех систем координат, неускоренных относительно инерциального пространства. В РФ можно выбрать любую точку как источник системы координат, затем настроить Декартовы (ортогональные) оси там.
Основной Simscape Multibody инерционная РФ называется Миром. Источник CS и триада оси также заданы в Мире. Мир может означать или РФ или CS, несмотря на то, что в большинстве контекстов, это означает систему Мировой координаты. Мир задает абсолютный отдых и универсальный координатный источник и оси, независимые от любых тел и территории в машине.
Общий синоним для системы координат работает система координат.
Теперь добавьте второй CS, названный O, источник которого переводит относительно Мирового источника и чьи оси вращаются относительно Мировых осей. Позже в этом разделе, этот второй CS идентифицирован с CS, зафиксированным в движущемся теле. (См. Переводы Органа по Представлению и Вращения.)
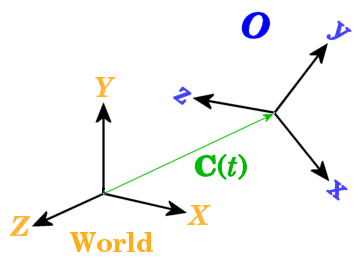
Векторный C представляет источник O. Его голова в начале координат O, и его хвост в Мировом начале координат. Источник O перемещается как произвольная функция времени C (t).
Ортогональные единичные векторы {u (x), u (y), u (z)} задают оси координат O.
Этот набор ориентирован относительно осей Мировой координаты на X, Y, Z, с единичными векторами {e (x), e (y), e (z)}. Ориентация изменяется со временем.
Можно выразить набор {u (x), u (y), u (z)} как линейная комбинация основания {e (x), e (y), e (z)} в терминах девяти коэффициентов. Они - отношения между векторами (не векторные компоненты) и независимы от системы координат и системы координат.
Вы получаете компоненты u в Мире путем проектирования u на e скалярными произведениями. Зависящие от времени коэффициенты R представляют ориентацию u относительно e. Можно использовать метки (1,2,3) в качестве эквивалентов для (x,y,z).
Компонентами любого векторного v, измеренного в Мире, является e (i) ·v. Представляйте их вектор-столбцом, Миром v. Компонентами v в O является u (i) ·v. Представляйте их вектор-столбцом, v O. Два набора компонентов связаны матричным преобразованием Мир v = R WO·vO. Содействующий R формирует матрицу, столбцы которой являются компонентами u в Мире:
Ортогональность и единичная длина гарантии u, что R является ортогональной матрицей вращения удовлетворяющий RR T = R TR = I, единичная матрица. R T является транспонированием R (строки и столбцы переключателя). Таким образом R-1 = R T.
Вращения всегда следуют за правилом правой руки, так, чтобы det (R) = +1.
Вы используете матрицы вращения в целом, чтобы преобразовать компоненты любого вектора от одного представления CS до другого, вращаемого представления CS.
К двум CSS наблюдателя, Миру и O, теперь добавляют третью точку p в произвольном движении. p мог представлять массу точки, центр тяжести (CG) расширенного тела или точка, зафиксированная в движущемся твердом теле, например. Эти два наблюдателя описывают движение этой точки по-разному, связанный друг с другом зависящими от времени преобразованиями координаты World-to-O.
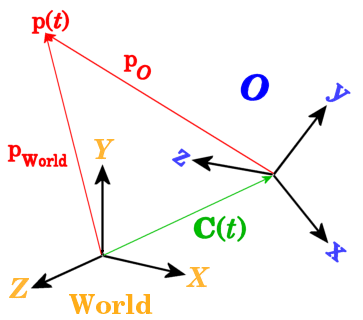
Компоненты p даны путем проектирования его на некоторых осях CS. Компоненты p, как измерено в Мире являются вектор-столбцом Мир p и, измеренные в O, являются вектор-столбцом p O. Эти два описания связаны
Таким образом движение, как измерено Миром p, когда преобразовано и наблюдается O как p O, имеет дополнительную временную зависимость, являющуюся результатом движения C и R.
Дифференцируйте отношение между Миром p и p O однажды относительно времени. Результат связывает скорость p, как измерено O к скорости, как измерено в Мире.
Раздел The Angular Velocity Тела из Его Матрицы Вращения объясняет, как выразить третий срок в более простой форме.
Затем считайте особый случай важным для описания движений твердого тела: движущаяся точка p фиксируется в самом теле. Позвольте O быть системой координат центра тяжести (CS CG) расширенного твердого тела (источник O в самом CG) и позволить p быть точкой, зафиксированной где-нибудь в том же теле. Эта фиксированная точка тела обозначается b в этом особом случае. Поскольку движущееся тело в целом ускоряется и с точки зрения перевода и вращательно, CS CG является неинерционным.
Матрица вращения R теперь описывает вращательное движение тела в терминах вращения осей CS CG относительно Мировых осей. Кроме того, потому что b теперь фиксируется в самом теле, это не перемещается в O: d b O/dt = 0. Все его движение, как замечено Миром должно неявно к движению R и C.
Продолжите идентифицировать O с CS CG тела и b как точка, зафиксированная в теле. Векторные компоненты b наблюдаются Миром как Мир b и CS CG как Тело b. В теле точка неподвижна: d b Body/dt = 0. Его скорость, наблюдаемая Миром, состоит из поступательного и вращательного движения целого твердого тела.
Поскольку RR T = I, (dR/dt) * R T + R (*dR T/dt) = 0. Вставьте R TR = I слева от Тела b и задайте антисимметричную матрицу Ω = +(dR/dt)*RT =-R* (dR T/dt). Его компоненты являются Ωik = + Σj ɛijkωj.
где ω является скоростью вращения тела в Мировом CS.
Движение Тела b разлагается в движение CG тела плюс угловое вращение Тела b относительно CG, все измеренные в Мире.
Отношение между производными времени вектора, измеренного в Мире и измеренного в теле, обычно содержит. Для любого вектора V,
Производная скорости вращения ω является угловым ускорением. Это - то же самое, ли измеренный в Мире или в теле, потому что = 0.
Символ сочетания ɛijk задан
ɛijk = +1, если ijk является ровным сочетанием (123 или каким-либо циклическим сочетанием этого)
ɛijk =-1, если ijk является нечетной подстановкой (321 или какое-либо циклическое сочетание этого)
ɛijk изменяет знак после переключения любых двух индексов и исчезает, если какие-либо два индекса равны. Компоненты перекрестного (векторного) продукта c = a X b двух векторов a и b
c i = Σjk ɛijkajbk