Exponenta Banner

PMSM

Постоянный магнит синхронный двигатель с синусоидальным распределением потока

расширьте все на странице
  • Библиотека:

  • Simscape / Электрический / Электромеханический / Постоянный магнит

Описание

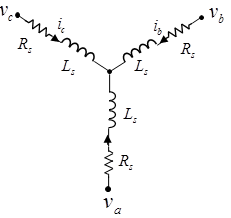
Блок PMSM моделирует постоянный магнит синхронный двигатель с трехфазным wye - статор раны. Рисунок показывает эквивалентную электрическую схему для обмоток статора.

Моторная конструкция

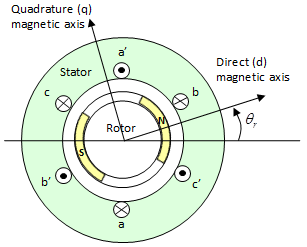
Этот рисунок показывает моторную конструкцию с однополюсно-парным на роторе.

Постоянные магниты генерируют магнитное поле ротора, которое создает синусоидальную скорость изменения потока с углом ротора.

Для соглашения осей в предыдущей фигуре a - выравниваются фаза и потоки постоянного магнита, когда угол механического устройства ротора, θr, является нулем. Блок поддерживает второе определение оси ротора, в котором угол механического устройства ротора задан как угол между a - фазой магнитная ось и ротором q - ось.

Уравнения

Напряжения через обмотки статора заданы:

[vavbvc]=[Rs000Rs000Rs][iaibic]+[dψadtdψbdtdψcdt],

где:

  • va, vb и vc являются отдельными напряжениями фазы через обмотки статора.

  • Rs является эквивалентным сопротивлением каждой обмотки статора.

  • ia, ib и ic являются токами, текущими в обмотках статора.

  • dψadt,dψbdt, и dψcdt скорости изменения магнитного потока в каждой обмотке статора.

Постоянный магнит и эти три обмотки способствуют общему потоку, соединяющему каждую обмотку. Общий поток задан:

[ψaψbψc]=[LaaLabLacLbaLbbLbcLcaLcbLcc][iaibic]+[ψamψbmψcm],

где:

  • ψa, ψb и ψc являются общими потоками, соединяющими каждую обмотку статора.

  • Laa, Lbb и Lcc являются самоиндукциями обмоток статора.

  • Lab, Lac, Lba, и так далее, является взаимной индуктивностью обмоток статора.

  • ψam, ψbm и ψcm являются потоками постоянного магнита, соединяющими обмотки статора.

Индуктивность в обмотках статора является функциями ротора электрический угол, заданный:

θe=Nθr,

Laa=Ls+Lmпотому что(2θe),

Lbb=Ls+Lmпотому что(2(θe−2π/3)),

Lcc=Ls+Lmпотому что(2(θe+2π/3)),

Lab=Lba=−Ms−Lmпотому что(2(θe+π/6)),

Lbc=Lcb=−Ms−Lmпотому что(2(θe+π/6−2π/3)),

и

Lca=Lac=−Ms−Lmпотому что(2(θe+π/6+2π/3)),

где:

  • θr является углом механического устройства ротора.

  • θe является ротором электрический угол.

  • Ls является самоиндукцией статора на фазу. Это значение является средней самоиндукцией каждой из обмоток статора.

  • Lm является колебанием индуктивности статора. Это значение является амплитудой колебания самоиндукции и взаимной индуктивности с изменяющимся углом ротора.

  • Ms является статором взаимная индуктивность. Это значение является средней взаимной индуктивностью между обмотками статора.

Поток постоянного магнита, соединяющий извилистый a, является максимумом когда θe = 0 ° и нуль когда θe = 90 °. Поэтому соединенный моторный поток задан:

[ψamψbmψcm]=[ψmпотому чтоθeψmпотому что(θe−2π/3)ψmпотому что(θe+2π/3)].

где ψm является потокосцеплением постоянного магнита.

Упрощенные электрические уравнения

Применение преобразования Парка с блоком, электрические уравнения производят выражение для крутящего момента, который независим от угла ротора.

Преобразование парка задано:

P=2/3[потому чтоθeпотому что(θe−2π/3)потому что(θe+2π/3)−sinθe−sin(θe−2π/3)−sin(θe+2π/3)0.50.50.5].

где θe является электрическим углом, заданным как Nθr. N является количеством пар полюса.

Используя преобразование Парка на статоре извилистые напряжения и токи преобразовывают их к системе координат dq0, которая независима от угла ротора:

[vdvqv0]=P[vavbvc]

и

[idiqi0]=P[iaibic].

Применение преобразования Парка к первым двум электрическим уравнениям производит следующие уравнения, которые задают поведение блока:

vd=Rsid+Lddiddt−NωiqLq,

vq=Rsiq+Lqdiqdt+Nω(idLd+ψm),

v0=Rsi0+L0di0dt,

и

T=32N(iq(idLd+ψm)−idiqLq),


где:

  • Ld = Ls + Ms + 3/2 Lm. Ld является статором d - индуктивность оси.

  • Lq = Ls + Ms − 3/2 Lm. Lq является статором q - индуктивность оси.

  • L0 = Ls – 2Ms. L0 является индуктивностью нулевой последовательности статора.

  • ω является скоростью вращательного механического устройства ротора.

  • N является количеством пар полюса постоянного магнита ротора.

  • T является крутящим моментом ротора. Крутящий момент течет из моторного случая (блокируйте физический порт C) к моторному ротору (блокируют физический порт R).

Использование блока PMSM исходная, неортогональная реализация Парка преобразовывает. При попытке применить альтернативную реализацию, вы получаете различные результаты для dq0 напряжения и токов.

Альтернативная параметризация потокосцепления

Можно параметризовать двигатель с помощью обратной эдс или закрутить константы, которые чаще всего даются на моторных таблицах данных при помощи опции Permanent magnet flux linkage.

Постоянная обратная эдс задана как пиковое напряжение, вызванное постоянным магнитом в каждой из фаз на модульную скорость вращения. Это связано с пиковым потокосцеплением постоянного магнита:

ke=Nψm.

Из этого определения, из этого следует, что обратной эдс eph для одной фазы дают:

eph=keω.

Постоянный крутящий момент задан как пиковый крутящий момент, вызванный каждой из фаз на текущий модуль. Это численно идентично в значении обратной эдс, постоянной, когда оба выражаются в единицах СИ:

kt=Nψm.

Когда Ld =Lq, и когда токи во всех трех фазах сбалансированы, из этого следует, что объединенным крутящим моментом T дают:

T=32ktiq=32ktIpk,

где Ipk является максимальным током в любой из этих трех обмоток.

Фактор 3/2 следует из этого являющегося установившейся суммой крутящих моментов от всех фаз. Поэтому крутящий момент постоянный kt мог также быть задан как:

kt=23(TIpk),

где T является измеренным общим крутящим моментом при тестировании со сбалансированным трехфазным током с пиковым линейным напряжением Ipk. Запись в терминах линейного напряжения RMS:

kt=23(Tiline,rms).

Переменные

Используйте настройки Variables, чтобы задать приоритет и начальные целевые значения для переменных в блоках перед симуляцией. Для получения дополнительной информации смотрите Приоритет Набора и Начальную Цель для Переменных в блоках (Simscape).

Порты

Сохранение

развернуть все

Расширяемый трехфазный порт.

Электрический порт сохранения сопоставлен с нейтральной фазой.

Порт сохранения вращательного механического устройства сопоставлен с моторным ротором.

Порт сохранения вращательного механического устройства сопоставлен с моторным случаем.

Параметры

развернуть все

Основной

Выберите настройку для обмоток:

  • Wye-wound — Обмотками является wye - рана.

  • Delta-wound — Обмотки являются раной дельты. a - фаза соединяется между портами a и b, b - фазой между портами b и c и c - фаза между портами c и a.

Количество постоянного магнита подпирает пары шестами на роторе.

Выберите Specify flux linkage, Specify torque constant, или Specify back EMF constant.

Пиковое потокосцепление постоянного магнита с любой из обмоток статора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Permanent magnet flux linkage на Specify flux linkage.

Крутящий момент, постоянный с любой из обмоток статора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Permanent magnet flux linkage на Specify torque constant.

Обратная эдс, постоянная с любой из обмоток статора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Permanent magnet flux linkage на Specify back EMF constant.

Выберите Specify Ld, Lq, and L0 или Specify Ls, Lm, and Ms.

Индуктивность D-оси.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ld, Lq, and L0.

Индуктивность Q-оси.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ld, Lq, and L0.

Индуктивность нулевой последовательности.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ld, Lq, and L0.

Средняя самоиндукция каждой из трех обмоток статора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ls, Lm, and Ms.

Амплитуда колебания самоиндукции и взаимной индуктивности обмоток статора с углом ротора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ls, Lm, and Ms.

Средняя взаимная индуктивность между обмотками статора.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Stator parameterization на Specify Ls, Lm, and Ms.

Сопротивление каждой из обмоток статора.

Опция, чтобы включать или исключить условия нулевой последовательности.

  • Include — Включайте условия нулевой последовательности. Чтобы приоритизировать точность модели, используйте эту настройку по умолчанию. Используя эту опцию:

  • Exclude — Исключите условия нулевой последовательности. Чтобы приоритизировать скорость симуляции для настольной симуляции или развертывания приложений, выберите эту опцию.

Контрольная точка для углового измерения ротора. Значением по умолчанию является Angle between the a-phase magnetic axis and the d-axis. Это определение показывают в Моторной фигуре Конструкции. Когда вы выбираете это значение, ротор и a - потоки фазы выравниваются, когда угол ротора является нулем.

Другим значением, которое можно выбрать для этого параметра, является Angle between the a-phase magnetic axis and the q-axis. Когда вы выбираете это значение, a - текущая фаза генерирует максимальный крутящий момент, когда угол ротора является нулем.

Механическое устройство

Инерция ротора присоединяется к механическому поступательному порту R. Значение может быть нулем.

Ротационное затухание.

Примеры модели

Electric Power Assisted Steering

Электроэнергия помогла регулированию

Используйте Постоянный магнит синхронный двигатель (PMSM), чтобы усилить приложенную силу драйвера в автомобильной руководящей системе с усилителем.

Открытая модель
Three-Phase PMSM Drive

Трехфазный диск PMSM

Постоянный магнит синхронная машина (PMSM) и инвертор измерены для использования в типичном гибридном автомобиле. Здесь инвертор соединяется непосредственно с батареей транспортного средства, но часто существует также промежуточный этап конвертера DC-DC. Модель может использоваться, чтобы спроектировать контроллер PMSM, выбирая архитектуру и усиления, чтобы достигнуть желаемой производительности. Чтобы проверять синхронизацию поворота IGBT - на и выключить, устройства IGBT могут быть непосредственно заменены более подробным блоком N-Channel IGBT. Для полного моделирования транспортного средства блок Servomotor может использоваться, чтобы абстрагировать PMSM, инвертор и контроллер с основанной на энергии моделью. Резистор Gmin обеспечивает очень маленькую проводимость, чтобы основываться, который улучшает числовые свойства модели при использовании решателя переменного шага.

Открытая модель
Parameterize a Permanent Magnet Synchronous Motor

Параметризуйте постоянный магнит синхронный двигатель

Оцените обратную эдс и закрутите константы постоянного магнита синхронного двигателя (PMSM) черного ящика с неизвестным потокосцеплением. Можно использовать или обратную эдс или закрутить постоянный, чтобы описать потокосцепление и параметризовать блок Simscape™ Electrical™ PMSM. Эта параметризация позволяет вам точно реплицировать поведение двигателя черного ящика в симуляцию.

Открыть скрипт

Ссылки

[1] Kundur, P. Устойчивость энергосистемы и управление. Нью-Йорк, Нью-Йорк: Макгроу Хилл, 1993.

[2] Андерсон, пополудни анализ неработающих энергосистем. Хобокен, NJ: нажатие Wiley-IEEE, 1995.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Блоки Simscape

Блоки

Темы

Введенный в R2013b

Документация Simscape Electrical
Поддержка