Создание КИХ-фильтра линейной фазы наименьших квадратов
b = firls(n,f,a)
b = firls(n,f,a,w)
b = firls(n,f,a,'ftype')
b = firls(n,f,a,w,'ftype')
firls проектирует КИХ-фильтр линейной фазы, который минимизирует взвешенную, интегрированную квадратичную невязку между идеальной кусочной линейной функцией и ответом величины фильтра по набору желаемых диапазонов частот.
b = firls(n,f,a) возвращает вектор-строку b содержа n+1 коэффициенты порядка n КИХ-фильтр, амплитудные частотой характеристики которого приблизительно совпадают с данными векторами f и a. Выходные коэффициенты фильтра или “касания”, в b повинуйтесь отношению симметрии.
Это тип I (n нечетный) и тип II (n даже) фильтры линейной фазы. Векторы f и a задайте амплитудные частотой характеристики фильтра:
f вектор пар точек частоты, заданных в области значений между 0 и 1, где 1 соответствует частоте Найквиста. Частоты должны быть в увеличивающемся порядке. Дублирующиеся точки частоты позволены и, на самом деле, могут использоваться, чтобы спроектировать фильтр точно то же самое как возвращенные fir1 и fir2 функции с прямоугольным (rectwin) окно.
a вектор, содержащий желаемую амплитуду в точках, заданных в f.
Желаемая амплитудная функция на частотах между парами точек (f (k), f (k +1)) для нечетного k является линейным сегментом, соединяющим точки (f (k), a (k)) и (f (k +1), a (k +1)).
Желаемая амплитудная функция на частотах между парами точек (f (k), f (k +1)) для k даже не задана. Это переход, или “не заботятся” об областях.
f и a та же длина. Эта длина должна быть четным числом.
firls всегда использует ровного порядка фильтра в настройках с полосой пропускания на частоте Найквиста. Это вызвано тем, что для нечетных порядков, частотная характеристика на частоте Найквиста обязательно 0. Если вы задаете n с нечетным знаком, firls шаг это 1.
Фигура ниже иллюстрирует отношение между f и a векторы в определении желаемого амплитудного ответа.
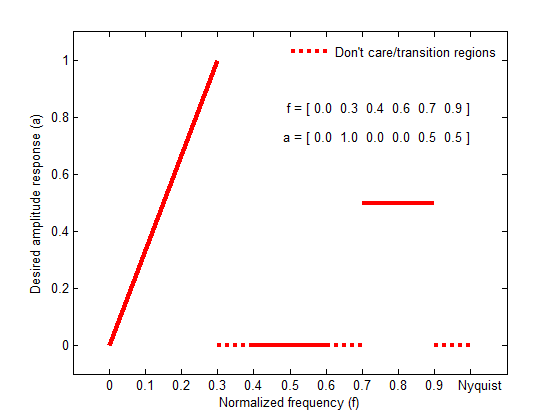
b = firls(n,f,a,w) использует веса в векторном w взвешивать подгонку в каждом диапазоне частот. Длина w половина длины f и a, таким образом, существует точно один вес на полосу.
b = firls(n,f,a, и'ftype')
b = firls(n,f,a,w, задайте тип фильтра, где 'ftype')'ftype' :
'hilbert' поскольку линейная фаза фильтрует с нечетной симметрией (тип III и IV типа). Выходные коэффициенты в b повинуйтесь отношению
Этот класс фильтров включает Гильбертов преобразователь, который имеет желаемую амплитуду 1 через целую полосу.
'differentiator' для типа III и фильтров IV типа, с помощью специального метода взвешивания. Для ненулевых амплитудных полос интегрированная квадратичная невязка имеет вес (1/f) 2 так, чтобы ошибка в низких частотах была намного меньше, чем в высоких частотах. Для КИХ-дифференциаторов, которые имеют амплитудную характеристику, пропорциональную частоте, фильтры минимизируют интегрированную квадратичную невязку родственника (интеграл квадрата отношения ошибки к желаемой амплитуде).
Спроектируйте КИХ фильтр lowpass порядка 255 с полосой перехода между и . Используйте fvtool отобразить величину и фазовые отклики фильтра.
b = firls(255,[0 0.25 0.3 1],[1 1 0 0]); fvtool(b,1,'OverlayedAnalysis','phase')
Идеальному дифференциатору дали частотную характеристику . Спроектируйте дифференциатор порядка 30, который ослабляет частоты выше . Включайте фактор в амплитуде, потому что частоты нормированы . Отобразите нулевой фазовый отклик фильтра.
b = firls(30,[0 0.9],[0 0.9*pi],'differentiator'); fvtool(b,1,'MagnitudeDisplay','zero-phase')
Спроектируйте 24-й порядок антисимметричный фильтр с кусочными линейными полосами пропускания.
F = [0 0.3 0.4 0.6 0.7 0.9];
A = [0 1.0 0.0 0.0 0.5 0.5];
b = firls(24,F,A,'hilbert');Постройте желаемые и фактические частотные характеристики.
[H,f] = freqz(b,1,512,2); plot(f,abs(H)) hold on for i = 1:2:6, plot([F(i) F(i+1)],[A(i) A(i+1)],'r--') end legend('firls design','Ideal') grid on xlabel('Normalized Frequency (\times\pi rad/sample)') ylabel('Magnitude')
Спроектируйте КИХ фильтр lowpass. Полоса пропускания лежит в диапазоне от DC до рад/выборка. Полоса задерживания располагается от рад/выборка к частоте Найквиста. Произведите три различных проекта, изменив веса полос в подгонке наименьших квадратов.
В первом проекте сделайте вес полосы задерживания выше, чем вес полосы пропускания фактором 100. Используйте эту спецификацию, когда очень важно, что ответ величины в полосе задерживания является плоским и близко к 0. Неравномерность в полосе пропускания приблизительно в 100 раз выше, чем пульсация полосы задерживания.
bhi = firls(18,[0 0.45 0.55 1],[1 1 0 0],[1 100]);
Во втором проекте инвертируйте веса так, чтобы вес полосы пропускания был 100 раз весом полосы задерживания. Используйте эту спецификацию, когда очень важно, что ответ величины в полосе пропускания является плоским и близко к 1. Пульсация полосы задерживания приблизительно в 100 раз выше, чем неравномерность в полосе пропускания.
blo = firls(18,[0 0.45 0.55 1],[1 1 0 0],[100 1]);
В третьем проекте дайте тот же вес обеим полосам. Результатом является фильтр с подобной пульсацией в полосе пропускания и полосе задерживания.
b = firls(18,[0 0.45 0.55 1],[1 1 0 0],[1 1]);
Визуализируйте ответы величины трех фильтров.
hfvt = fvtool(bhi,1,blo,1,b,1,'MagnitudeDisplay','Zero-phase'); legend(hfvt,'bhi: w = [1 100]','blo: w = [100 1]','b: w = [1 1]')
Одно из следующих диагностических сообщений отображено, когда неправильный аргумент используется:
F must be even length. F and A must be equal lengths. Requires symmetry to be 'hilbert' or 'differentiator'. Requires one weight per band. Frequencies in F must be nondecreasing. Frequencies in F must be in range [0,1].
Более серьезное предупреждающее сообщение
Warning: Matrix is close to singular or badly scaled.
Это имеет тенденцию происходить, когда продукт длины фильтра и ширины перехода становится большим. В этом случае коэффициенты фильтра b не могут представлять желаемый фильтр. Можно проверять фильтр путем рассмотрения его частотной характеристики.
Ссылка [1] описывает теоретический подход позади firls. Функция решает систему линейных уравнений, включающих матрицу скалярного произведения размера примерно n/2 использование MATLAB® \ оператор.
Эта функция проектирует тип I, II, III и фильтры линейной фазы IV. Тип I и II является значениями по умолчанию для n, четного и нечетного соответственно, в то время как 'hilbert' и 'differentiator' флаги производят тип III (n даже) и IV (n нечетный) фильтры. Различные типы фильтра имеют различные симметрии и ограничения на их частотные характеристики (см. [2] для деталей).
| Линейный тип фильтра фазы | Порядок фильтра | Симметрия коэффициентов | Ответ H (f), f = 0 | Ответ H (f), f = 1 (Найквист) |
|---|---|---|---|---|
Тип I | Даже | Никакое ограничение | Никакое ограничение | |
Тип II | Нечетный | Никакое ограничение | H (1) = 0 | |
Тип III | Даже | H (0) = 0 | H (1) = 0 | |
Введите IV | Нечетный | H (0) = 0 | Никакое ограничение |
[1] Парки, Томас В. и К. Сидни Беррус. Создание цифровых фильтров. Нью-Йорк: John Wiley & Sons, 1987, стр 54–83.
[2] Оппенхейм, Алан V, Рональд В. Шафер и Джон Р. Бак. Обработка сигналов дискретного времени. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1999.
fir1 | fir2 | firpm | rcosdesign