Обратное кратковременное преобразование Фурье
x = istft(___,Name,Value)
Сгенерируйте сигнал с тремя каналами, состоящий из трех различных щебетов, произведенных на уровне 1 кГц в течение 1 секунды.
Первый канал состоит из вогнутого квадратичного щебета с мгновенной частотой 100 Гц в t = 0 и пересекает 300 Гц в t = 1 секунда. Это имеет начальную фазу, равную 45 градусам.
Второй канал состоит из выпуклого квадратичного щебета с мгновенной частотой 200 Гц в t = 0 и пересекает 600 Гц в t = 1 секунда.
Третий канал состоит из логарифмического щебета с мгновенной частотой 300 Гц в t = 0 и пересекает 500 Гц в t = 1 секунда.
Вычислите STFT многоканального сигнала с помощью периодического Окна Хэмминга длины 256 и продолжительности перекрытия 15 выборок.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,'quadratic',45,'concave'); chirp(t,200,1,600,'quadratic',[],'convex'); chirp(t,300,1,500,'logarithmic')]'; [S,F,T] = stft(x,fs,'Window',hamming(256,'periodic'),'OverlapLength',15);
Постройте исходные и восстановленные версии первых и вторых каналов.
[ix,ti] = istft(S,fs,'Window',hamming(256,'periodic'),'OverlapLength',15); plot(t,x(:,1)','LineWidth',1.5) hold on plot(ti,ix(:,1)','r--') hold off legend('Original Channel 1','Reconstructed Channel 1')

plot(t,x(:,2)','LineWidth',1.5) hold on plot(ti,ix(:,2)','r--') legend('Original Channel 2','Reconstructed Channel 2')

Вокодер фазы выполняет время, простираясь и подачу, масштабирующуюся путем преобразования аудио в частотный диапазон. Эта схема показывает операции, вовлеченные в реализацию вокодера фазы.

Вокодер фазы берет STFT сигнала с аналитическим окном размера транзитного участка и затем выполняет ISTFT с окном синтеза размера транзитного участка . Вокодер таким образом использует в своих интересах метод ВОЛИ. К фрагменту времени сигнал аналитическое окно использует большее число выборок перекрытия, чем синтез. В результате существует больше выборок при выходе, чем во входе (), несмотря на то, что содержимое частоты остается то же самое. Теперь можно передать шкалу этот сигнал путем воспроизведения его на уровне более высокой частоты дискретизации, которая производит сигнал с исходной продолжительностью, но более высокой подачей.
Загрузите звуковой файл, содержащий фрагмент "Хора Аллилуйи Генделя", произведенного на уровне 8 192 Гц.
load handelСпроектируйте корневое-Hann окно длины 512. Установите аналитическую длину перекрытия как 192 и длину перекрытия синтеза как 166.
wlen = 512;
win = sqrt(hann(wlen,'periodic'));
noverlapA = 192;
noverlapS = 166;Реализуйте вокодер фазы при помощи аналитического окна перекрытия 192 и окна синтеза перекрытия 166.
S = stft(y,Fs,'Window',win,'OverlapLength',noverlapA); iy = istft(S,Fs,'Window',win,'OverlapLength',noverlapS); %To hear, type soundsc(w,Fs), pause(10), soundsc(iw,Fs);
Если окна анализа и синтеза будут тем же самым, но длина перекрытия изменяется, будет дополнительное усиление/потеря, которое необходимо будет настроить. Это - общий подход к реализации вокодера фазы.
Вычислите отношение транзитного участка и используйте его, чтобы настроить усиление восстановленного сигнала. Также вычислите частоту переключенных подачей данных с помощью отношения транзитного участка.
hopRatio = (wlen-noverlapS)/(wlen-noverlapA);
iyg = iy*hopRatio;
Fp = Fs*hopRatio;
%To hear, type soundsc(iwg,Fs), pause(15), soundsc(iwg,Fp);Постройте исходный сигнал и время расширенный сигнал с фиксированным усилением.
plot((0:length(iyg)-1)/Fs,iyg,(0:length(y)-1)/Fs,y) xlabel('Time (s)') xlim([0 (length(iyg)-1)/Fs]) legend('Time Stretched Signal with Fixed Gain','Original Signal','Location','best')

Сравните растянутый во времени сигнал и подачу переключенный сигнал на том же графике.
plot((0:length(iy)-1)/Fs,iy,(0:length(iy)-1)/Fp,iy) xlabel('Time (s)') xlim([0 (length(iyg)-1)/Fs]) legend('Time Stretched Signal','Pitch Shifted Signal','Location','best')

Чтобы лучше изучить эффект данных о сдвигающем подачи, считайте следующую синусоиду частоты Fs более чем 2 секунды.
t = 0:1/Fs:2; x = sin(2*pi*10*t);
Вычислите кратковременное преобразование Фурье и обратное кратковременное преобразование Фурье с длинами перекрытия 192 и 166 соответственно.
Sx = stft(x,Fs,'Window',win,'OverlapLength',noverlapA); ix = istft(Sx,Fs,'Window',win,'OverlapLength',noverlapS);
Постройте исходный сигнал на одном графике и растянутом во времени и подаче переключенный сигнал на другом.
subplot(2,1,1) plot((0:length(ix)-1)/Fs,ix,'LineWidth',2) xlabel('Time (s)') ylabel('Signal Amplitude') xlim([0 (length(ix)-1)/Fs]) legend('Time Stretched Signal') subplot(2,1,2) hold on plot((0:length(x)-1)/Fs,x) plot((0:length(ix)-1)/Fp,ix,'--','LineWidth',2) legend('Original Signal','Pitch Shifted Signal','Location','best') hold off xlabel('Time (s)') ylabel('Signal Amplitude') xlim([0 (length(ix)-1)/Fs])

Сгенерируйте комплексную синусоиду частоты 1 кГц и длительности 2 секунды.
fs = 1e3; ts = 0:1/fs:2-1/fs; x = exp(2j*pi*100*cos(2*pi*2*ts));
Спроектируйте периодическое окно Hann длины 100 и определите номер выборок перекрытия к 75. Проверяйте окно и длину перекрытия для податливости COLA.
nwin = 100;
win = hann(100,'periodic');
noverlap = 75;
tf = iscola(win,noverlap)tf = logical
1
Нулевая клавиатура сигнал удалить краевые эффекты. Чтобы избежать усечения, заполните входной сигнал нулями, таким образом что целое число. Установите длину БПФ на 128. Вычислите кратковременное преобразование Фурье комплексного сигнала.
xZero = [zeros(1,nwin) x zeros(1,nwin)]; fftlen = 128; s = stft(xZero,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);
Вычислите обратное кратковременное преобразование Фурье и удалите нули для совершенной реконструкции.
[is,ti] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen); is(1:nwin) = []; is(end-nwin+1:end) = []; ti = ti(1:end-2*nwin);
Постройте действительные части исходных и восстановленных сигналов. Мнимая часть сигнала также восстановлена отлично.
plot(ts,real(x)) hold on plot(ti,real(is),'--') xlim([0 0.5]) xlabel('Time (s)') ylabel('Amplitude (V)') legend('Original Signal','Reconstructed Signal') hold off

Сгенерируйте синусоиду, произведенную на уровне 2 кГц в течение 1 секунды.
fs = 2e3; t = 0:1/fs:1-1/fs; x = 5*sin(2*pi*10*t);
Спроектируйте периодическое Окно Хэмминга длины 120. Проверяйте ограничение COLA на окно с перекрытием 80 выборок. Комбинацией перекрытия окна является совместимый COLA.
win = hamming(120,'periodic');
noverlap = 80;
tf = iscola(win,noverlap)tf = logical
1
Установите длину БПФ на 512. Вычислите кратковременное преобразование Фурье.
fftlen = 512; s = stft(x,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);
Вычислите обратное кратковременное преобразование Фурье.
[X,T] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen,'Method','ola','ConjugateSymmetric',true);
Постройте исходные и восстановленные сигналы.
plot(t,x,'b') hold on plot(T,X,'-.r') xlabel('Time (s)') ylabel('Amplitude (V)') title('Original and Reconstructed Signal') legend('Original Signal','Reconstructed Signal') hold off

s — Кратковременное преобразование ФурьеКратковременное преобразование Фурье, заданное как матрица или трехмерный массив. Для одноканальных сигналов задайте s как матрица со временем, увеличиваясь через столбцы и частоту, увеличивающую вниз строки. Для многоканальных сигналов задайте s как трехмерный массив с третьей размерностью, соответствующей каналам. Частота и временные векторы получены как выходные параметры stft.
Если вы инвертируете s использование istft и хочу результат быть той же длиной как x, значение (length(x)-noverlap)/(length(window)-noverlap) должно быть целое число.
Типы данных: double | single
Поддержка комплексного числа: Да
fs — Частота дискретизацииЧастота дискретизации в герц, заданном как положительная скалярная величина.
Типы данных: double | single
ts 'SampleTime' Шаг расчета, заданный как duration скаляр.
Пример: seconds(1) duration
Типы данных: duration
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
istft(s,'Window',win,'OverlapLength',50,'FFTLength',128) окна данные с помощью окна win, с 50 выборками накладываются между смежными сегментами и 128 БПФ точки.'Window' — Функция работы с окнамиhann(128,'periodic') (значение по умолчанию) | векторФункция работы с окнами, заданная как разделенная запятой пара, состоящая из 'Window' и вектор. Если вы не задаете окно или задаете его как пустой, функция использует периодическое окно Hann длины 128. Длина Window должен быть больше или быть равен 2.
Для списка доступных окон смотрите Windows.
Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Hann длины N + 1.
Типы данных: double | single
'OverlapLength' — Количество перекрытых выборокКоличество перекрытых выборок, заданных как разделенная запятой пара, состоящая из OverlapLength и положительное целое число, меньшее, чем длина window. Если вы не используете 'OverlapLength' или задайте его как пустой, это установлено в самое большое целое число меньше чем 75% длины окна, которая оказывается 96 выборками для окна Hann по умолчанию.
Типы данных: double | single
'FFTLength' — Количество точек ДПФКоличество точек ДПФ, заданных как разделенная запятой пара, состоящая из FFTLength и положительное целое число. Чтобы достигнуть совершенной реконструкции временного интервала, необходимо установить FFTLength совпадать с используемым в stft.
Типы данных: double | single
'Method' — Метод перекрытия - добавляет'wola' (значение по умолчанию) | 'ola'Метод перекрытия - добавляет, заданный как разделенная запятой пара, состоящая из Method и одно из следующего:
'wola' — Взвешенное перекрытие - добавляет
'ola' — Перекрытие - добавляет
'ConjugateSymmetric' — Сопряженная симметрия исходного сигналаfalse (значение по умолчанию) | trueСопряженная симметрия исходного сигнала, заданного как разделенная запятой пара, состоящая из ConjugateSymmetric и true или false. Если эта опция установлена в true, istft принимает что вход s симметрично, в противном случае никакое симметричное предположение не сделано. Когда s не точно сопряжен симметричный из-за ошибки округления, устанавливая пару "имя-значение" на true гарантирует, что STFT обработан, как будто это было сопряжено симметричный. Если s сопряжен симметричный, затем обратный расчет преобразования быстрее, и выход действителен.
'Centered' — Частотный диапазонtrue (значение по умолчанию) | falseЧастотный диапазон, заданный как разделенная запятой пара, состоящая из Centered и true или false. Если эта опция установлена в true, затем спектр сосредоточен и вычисляется на интервале-π к π. В противном случае спектр вычисляется на интервале 0 к 2π.
'InputTimeDimension' — Введите измерение времениВведите измерение времени, заданное как разделенная запятой пара, состоящая из InputTimeDimension и acrosscolumns или downrows. Если это значение установлено к downrows, istft принимает что измерение времени s снижается на строки, и частота через столбцы. Если это значение установлено к acrosscolumns, функциональный istft принимает что измерение времени s через столбцы, и размерность частоты снижается на строки.
x — Восстановленный сигналВосстановленный сигнал во временном интервале, возвращенном как вектор или матрица.
Типы данных: single | double
t — Моменты времениМоменты времени, возвращенные как вектор.
Если частота дискретизации fs обеспечивается, затем t содержит временные стоимости в секундах.
Если длительность ts обеспечивается, затем t имеет тот же формат времени как входная длительность и массив длительности.
Если никакая информация времени не предоставляется, то t содержит демонстрационные числа.
Типы данных: double | single
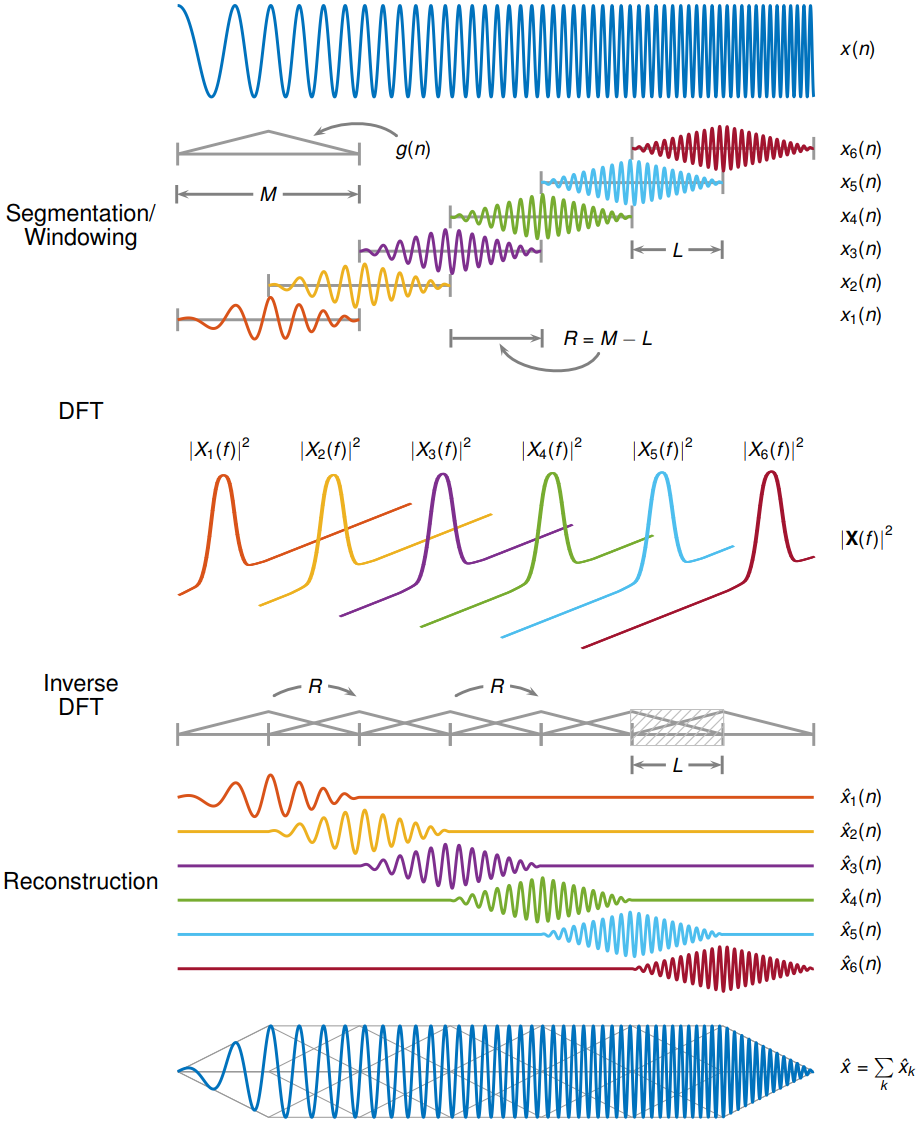
Обратное кратковременное преобразование Фурье вычисляется путем взятия ОБПФ каждого вектора ДПФ STFT и добавления перекрытия инвертированные сигналы. ISTFT вычисляется можно следующим образом:
где размер транзитного участка между последовательными ДПФ, ДПФ оконных данных, сосредоточенных во время и . Обратный STFT является совершенной реконструкцией исходного сигнала пока где analysis window использовался к окну исходный сигнал и константа. Следующая фигура изображает шаги, выполненные в восстановлении исходного сигнала.
Чтобы гарантировать успешную реконструкцию немодифицированных спектров, аналитическое окно должно удовлетворить ограничению COLA. В общем случае, если аналитическое окно удовлетворяет условию , окно считается совместимым КОЛОЙ. Кроме того, податливость COLA может быть описана или как слабая или как сильная.
Слабая податливость COLA подразумевает, что преобразование Фурье аналитического окна имеет нули в гармониках частоты кадров, таким образом что
Отмена псевдонима нарушена спектральными модификациями. Слабый COLA использует отмену псевдонима в частотном диапазоне. Поэтому совершенная реконструкция является возможным использованием слабо совместимых КОЛОЙ окон, пока сигнал не подвергся никаким спектральным модификациям.
Для сильной податливости COLA преобразование Фурье окна должно последовательно быть bandlimited с субдискретизацией частотой кадров, таким образом что
Это уравнение показывает, что никакое искажение не позволено сильным ограничением COLA. Кроме того, для сильной податливости COLA, значения константы должен равняться 1. В общем случае, если кратковременный спектр изменяется в каком-либо случае, более сильный COLA, совместимое окно предпочтено.
Можно использовать iscola функционируйте, чтобы проверять на слабую податливость COLA. Количество суммирования, используемого, чтобы проверить соответствие COLA, диктуют длина окна и размер транзитного участка. В общем случае распространено использовать \in для взвешенного перекрытия - добавляют (ВОЛЯ), и для перекрытия - добавляют (OLA). По умолчанию, istft использует метод ВОЛИ, путем применения synthesis window прежде, чем выполнить метод перекрытия-суммы.
В общем случае окно синтеза совпадает с аналитическим окном. Можно создать полезные окна ВОЛИ путем пущения квадратного корня из сильного окна OLA. Можно использовать этот метод во всех неотрицательных окнах OLA. Например, корневое-Hann окно является хорошим примером окна ВОЛИ.
В общем случае вычисление STFT входного сигнала и инвертирование его не приводят к совершенной реконструкции. Если вы хотите, чтобы выход ISTFT совпадал с исходным входным сигналом максимально тесно, сигнал и окно должны удовлетворить следующим условиям:
Введите размер — Если вы инвертируете выход stft использование istft и хочу результат быть той же длиной как входной сигнал x, значение должно быть целое число.
Податливость COLA — Использование совместимые КОЛОЙ окна, принимая, что вы не изменили кратковременное преобразование Фурье сигнала.
Дополнение — Если длина входного сигнала такова, что значение k не является целым числом, нулевая клавиатура сигнал прежде, чем вычислить кратковременное преобразование Фурье. Удалите дополнительные нули после инвертирования сигнала.
[1] Crochiere, R. E. “Взвешенный Метод перекрытия-суммы Кратковременного Анализа/Синтеза Фурье”. Транзакции IEEE на Акустике, Речи и Обработке сигналов. Издание 28, № 1, февраль 1980, стр 99–102.
[2] Гриффин, D. W. и Дж. С. Лим. “Оценка сигнала от Модифицированного Кратковременного преобразования Фурье”. Транзакции IEEE на Акустике, Речи и Обработке сигналов. Издание 32, № 2, апрель 1984, стр 236–243.
[3] Портнофф, M. R. “Представление частоты времени Цифровых сигналов и Систем На основе Кратковременного анализа Фурье”. Транзакции IEEE на Акустике, Речи и Обработке сигналов. Издание 28, № 1, февраль 1980, стр 55–69.
[4] Смит, Обработка Звукового сигнала Дж. О. Спектрэла. https://ccrma.stanford.edu / ~ jos/sasp/, онлайновая книга, 2 011 выпусков, получил доступ к ноябрю 2018.
[5] А. Д. Гоцен, Н. Бернардини и Д. Арфиб, “Традиционные реализации вокодера фазы: приемы торговли”, продолжения COST G-6 конференция по эффектам цифрового аудио (DAFX-00), Вероне, Италия, 7-9 декабря 2000.
[6] Шарп, Брюс. Обратимость Перекрытия - Добавляет Обработку. https://gauss256.github.io/blog/cola.html, июль 2019, к которому получают доступ.
Указания и ограничения по применению:
'ConjugateSymmetric' аргумент не поддержан для генерации кода.
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.