Постройте неявное символьное уравнение или функцию
fimplicit( строит неявное символьное уравнение или функциональный f)f на интервале по умолчанию [-5 5] для x и y.
fimplicit( графики f,[xmin xmax
ymin ymax])f на интервале xmin <x <xmax и ymin <y <ymax. fimplicit функционируйте использует symvar заказать интервалы присвоения и переменные.
fimplicit(___, использование LineSpec)LineSpec установить стиль линии, символ маркера и цвет линии.
fimplicit(___, задает свойства линии с помощью одного или нескольких Name,Value)Name,Value парные аргументы. Используйте эту опцию с любыми комбинациями входных аргументов в предыдущих синтаксисах. Name,Value парные настройки применяются ко всем построенным графикам. Чтобы установить опции для отдельных линий, используйте объекты, возвращенные fimplicit.
fimplicit( графики в оси заданы ax,___)ax вместо текущей системы координат gca.
fi = fimplicit(___)
Постройте гиперболу при помощи fimplicit. fimplicit функционируйте использует интервал по умолчанию для и .
syms x y fimplicit(x^2 - y^2 == 1)

Постройте гиперболу, описанную функцией первым объявлением символьного функционального f(x,y) использование syms. fimplicit функционируйте использует интервал по умолчанию для и .
syms f(x,y)
f(x,y) = x^2 - y^2 - 1;
fimplicit(f)
Постройте половину круга при помощи интервалов и . Задайте интервал графического вывода в качестве второго аргумента fimplicit.
syms x y circle = x^2 + y^2 == 3; fimplicit(circle, [-4 0 -2 2])

Можно построить несколько уравнений или путем передачи входных параметров как вектора или при помощи hold on последовательно построить на той же фигуре. Если вы задаете LineSpec и аргументы Name-Value, они применяются ко всем линиям. Чтобы установить опции для индивидуальных участков, используйте указатели на функцию, возвращенные fimplicit.
Разделите фигуру на два подграфика при помощи subplot. На первом подграфике, графике и использование векторного входа. На втором подграфике постройте те же входные параметры при помощи hold on.
syms x y circle1 = x^2 + y^2 == 1; circle2 = x^2 + y^2 == 3; subplot(2,1,1) fimplicit([circle1 circle2]) title('Multiple Equations Using Vector Input') subplot(2,1,2) fimplicit(circle1) hold on fimplicit(circle2) title('Multiple Equations Using hold on Command') hold off

Постройте три концентрических круга увеличивающегося диаметра. Для первой линии используйте linewidth 2. Для второго задайте пунктирный стиль красной линии с круговыми маркерами. Для третьего задайте голубой стиль штрихпунктирной линии с маркерами звездочки. Отобразите легенду.
syms x y circle = x^2 + y^2; fimplicit(circle == 1, 'Linewidth', 2) hold on fimplicit(circle == 2, '--or') fimplicit(circle == 3, '-.*c') legend('show','Location','best') hold off

График . Задайте выход, чтобы сделать fimplicit возвратите объект графика.
syms x y eqn = y*sin(x) + x*cos(y) == 1; fi = fimplicit(eqn)

fi =
ImplicitFunctionLine with properties:
Function: [1x1 sym]
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Show all properties
Измените нанесенное на график уравнение в при помощи записи через точку, чтобы установить свойства. Точно так же измените цвет линии в красный и стиль линии к штрихпунктирной линии. Горизонтальные и вертикальные линии в выходе являются артефактами, которые должны быть проигнорированы.
fi.Function = x/cos(y) + y/sin(x) == 0; fi.Color = 'r'; fi.LineStyle = '-.';

График на интервале и . Добавьте заголовок и подписи по осям. Создайте метки деления оси X путем охвата пределов оси X с промежутками в pi/2. Отобразите эти метки деления при помощи XTick свойство. Создайте метки оси X при помощи arrayfun применять texlabel к S. Отобразите эти метки при помощи XTickLabel свойство. Повторите эти шаги для оси Y.
Чтобы использовать LATEX в графиках, смотрите latex.
syms x y eqn = x*cos(y) + y*sin(x) == 1; fimplicit(eqn, [-2*pi 2*pi]) grid on title('x cos(y) + y sin(x) for -2\pi < x < 2\pi and -2\pi < y < 2\pi') xlabel('x') ylabel('y') ax = gca; S = sym(ax.XLim(1):pi/2:ax.XLim(2)); ax.XTick = double(S); ax.XTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false); S = sym(ax.YLim(1):pi/2:ax.YLim(2)); ax.YTick = double(S); ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

Когда вы масштабируете в график, fimplicit переоценивает график автоматически. Эта переоценка на изменении масштаба может показать скрытую деталь в меньших масштабах.
Разделите фигуру на два при помощи subplotграфик и в первых и во вторых подграфиках. Масштабируйте во второй подграфик при помощи zoom. Масштабируемый подграфик показывает деталь, которая не отображается в первом подграфике.
syms x y eqn = x*cos(y) + y*sin(1/x) == 0; subplot(2,1,1) fimplicit(eqn) subplot(2,1,2) fimplicit(eqn) zoom(2)

f — Неявное уравнение или функция, чтобы построитьНеявное уравнение или функция, чтобы построить, заданный как символьное уравнение, выражение или функция. Если правая сторона не задана, то она принята, чтобы быть 0.
[min max] — Графический вывод области значений для x и yГрафический вывод области значений для x и y, заданный как вектор двух чисел. Областью значений по умолчанию является [-5 5].
[xmin xmax ymin ymax] — Графический вывод области значений для x и yГрафический вывод области значений для x и y, заданный как вектор четырех чисел. Областью значений по умолчанию является [-5 5 -5 5].
ax Объект осейОбъект осей. Если вы не задаете объект осей, то fimplicit использует текущую систему координат gca.
LineSpec — Спецификация линииСпецификация линии, заданная как вектор символов или строка со стилем линии, маркером и цветом. Элементы могут появиться в любом порядке, и можно не использовать одну или несколько опций. Чтобы показать только маркеры без соединительных линий, задайте маркер и не используйте стиль линии.
Пример: 'r--o' задает красный цвет, пунктирную линию и круговые маркеры
| Спецификатор стиля линии | Описание |
|---|---|
- | Сплошная линия (значение по умолчанию) |
-- | Пунктирная линия |
: | Пунктирная линия |
-. | Штрихпунктирная линия |
| Спецификатор маркера | Описание |
|---|---|
o | Круг |
+ | Знак «плюс» |
* | Звездочка |
. | Точка |
x | Крест |
s | Квадрат |
d | Ромб |
^ | Треугольник, направленный вверх |
v | Нисходящий треугольник |
> | Треугольник, указывающий вправо |
< | Треугольник, указывающий влево |
p | Пентаграмма |
h | Гексаграмма |
| \color{specifier} | Описание |
|---|---|
| желтый |
| пурпурный |
| голубой |
| красный |
| зеленый |
| синий |
| белый |
| черный |
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'Marker','o','MarkerFaceColor','red'Функциональные свойства линии, перечисленные здесь, являются только подмножеством. Для полного списка смотрите ImplicitFunctionLine Properties.
'MeshDensity' — Количество оценки указывает на направлениеКоличество оценки указывает на направление, заданное как номер. Значением по умолчанию является 151.
'Color' 'LineColor' 'r' | 'g' | 'b' | ...Цвет линии, заданный как триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или скаляром строки, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan' | 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию использованием MATLAB® во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Пример: 'blue'
Пример: [0 0 1]
Пример: '#0000FF'
'LineStyle' — Стиль линии'-' (значение по умолчанию) | '--' | ':' | '-.' | 'none'Стиль линии, заданный как одна из опций, перечислен в этой таблице.
| Стиль линии | Описание | Получившаяся линия |
|---|---|---|
'-' | Сплошная линия |
|
'--' | Пунктирная линия |
|
':' | Пунктирная линия |
|
'-.' | Штрих-пунктирная линия |
|
'none' | Никакая линия | Никакая линия |
'LineWidth' 'LineWidth' Ширина линии, заданная как положительное значение в точках, где 1 точка = 1/72 дюйма. Если у линии есть маркеры, ширина линии также влияет на края маркера.
'Marker' — Символ маркера'none' (значение по умолчанию) | 'o' | '+' | '*' | '.' | 'x' | 's' | 'd' | ...Символ маркера, заданный как одно из значений в этой таблице. По умолчанию линия не имеет маркеров. Добавьте маркеры в выбранных точках вдоль линии путем определения маркера.
| Значение | Описание |
|---|---|
'o' | Круг |
'+' | Знак «плюс» |
'*' | Звездочка |
'.' | Точка |
'x' | Крест |
'square' или 's' | Квадрат |
'diamond' или 'd' | Ромб |
'^' | Треугольник, направленный вверх |
'v' | Нисходящий треугольник |
'>' | Треугольник, указывающий вправо |
'<' | Треугольник, указывающий влево |
'pentagram' или 'p' | Пятиконечная звезда (пентаграмма) |
'hexagram' или 'h' | Шестиконечная звезда (гексаграмма) |
'none' | Никакие маркеры |
'MarkerEdgeColor' — Цвет контура маркера'auto' (значение по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет контура маркера, заданный как 'auto', триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название. Значение по умолчанию 'auto' использует тот же цвет в качестве Color свойство.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или скаляром строки, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Не применяется | Не применяется | Не применяется | Нет цвета |
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию использованием MATLAB во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
'MarkerFaceColor' — Цвет заливки маркера'none' (значение по умолчанию) | 'auto' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет заливки маркера, заданный как 'auto', триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название. 'auto' значение использует тот же цвет в качестве MarkerEdgeColor свойство.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или скаляром строки, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Не применяется | Не применяется | Не применяется | Нет цвета |
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию использованием MATLAB во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Example: [0.3 0.2 0.1]
Пример: 'green'
Пример: '#D2F9A7'
'MarkerSize' 'MarkerSize' Размер маркера, заданный как положительное значение в точках, где 1 точка = 1/72 дюйма.
fi — Один или несколько объектов линии неявной функцииОдин или несколько объектов линии неявной функции, возвращенных как скаляр или вектор. Можно использовать эти объекты запросить и изменить свойства определенной линии. Для списка свойств смотрите ImplicitFunctionLine Properties.
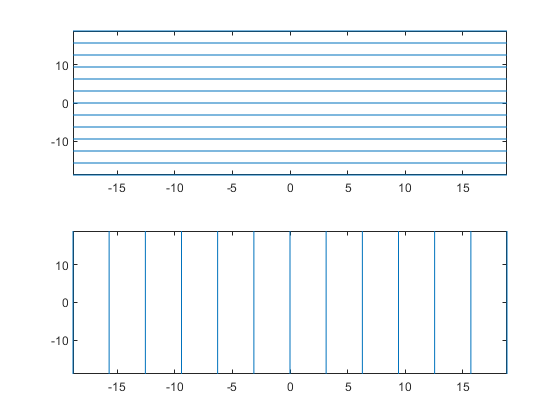
fimplicit присваивает символьные переменные в f к x ось, затем y ось и symvar определяет порядок переменных, которые будут присвоены. Поэтому переменная и имена оси не могут соответствовать. Обеспечивать fimplicit чтобы присвоить x или y к его соответствующей оси, создайте символьную функцию, чтобы построить, затем передать символьную функцию fimplicit.
Например, следующий код строит корни неявной функции f (x, y) = sin (y) двумя способами. Первый путь обеспечивает волны, чтобы колебаться относительно оси y. Второй путь присваивает y оси x, потому что это является первым (и только) переменная в символьной функции.
syms x y; f(x,y) = sin(y); intvl = [-6 6]*pi; figure; subplot(2,1,1) fimplicit(f,intvl); subplot(2,1,2) fimplicit(f(x,y),intvl); % Or fimplicit(sin(y) == 0,intvl);
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.