bernoulliБернуллиевые числа и полиномы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
bernoulli(n) bernoulli(n,x)
bernoulli(n) возвращает n-th Бернуллиевый номер.
bernoulli(n, x) возвращает n-th Бернуллиевый полином в x.
Бернуллиевые полиномы заданы производящей функцией
.
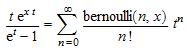Бернуллиевые числа заданы bernoulli(n) = bernoulli(n,0).
Ошибка происходит если n численное значение, не представляющее неотрицательное целое число.
Если n целое число, больше, чем значение, возвращенное Pref::autoExpansionLimit(), затем вызов bernoulli(n) возвращен символически. Используйте expand(bernoulli(n)) получить явный числовой результат для больших целых чисел n.
Если n содержит нечисловые символьные идентификаторы, затем вызов bernoulli(n) возвращен символически. В большинстве случаев то же самое сохраняется для вызовов bernoulli(n, x). Некоторые упрощения реализованы для специальных численных значений, таких как x = 0, x = 1/2, x = 1 и т.д. для символьного n . См. пример 3.
Обратите внимание на то, что оценка с плавающей точкой для полиномов высокой степени может быть численно неустойчивой. См. Пример 4.
Оценка с плавающей точкой на стандартном интервале x ∈ [0, 1] численно устойчив для произвольного n.
Когда названо значением с плавающей точкой x, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
Первые Бернуллиевые числа:
bernoulli(n) $ n = 0..11
Первые Бернуллиевые полиномы:
bernoulli(n, x) $ n = 0..4
Если n является символьным, затем отвечают на символьный звонок:
bernoulli(n, x), bernoulli(n + 3/2, x), bernoulli(n + 5*I, x)
Если x не неопределенное, затем оценка Бернуллиевого полинома в точке x возвращен:
bernoulli(50, 1 + I)
bernoulli(3, 1 - y), expand(bernoulli(3, 1 - y))
Определенные упрощения происходят для некоторых специальных численных значений x, даже если n является символьным:
bernoulli(n, 0), bernoulli(n, 1/2), bernoulli(n, 1)
Вызовы с числовыми аргументами между
и 1 автоматически переписаны в терминах вызовов с аргументами между 0 и
:
bernoulli(n, 2/3), bernoulli(n, 0.7)
Вызовы с отрицательными числовыми аргументами automatially переписаны в терминах вызовов с положительными аргументами:
bernoulli(n, -2)
bernoulli(n, -12.345)
Оценка плавающая знатные полиномы может быть численно неустойчивой:
exact := bernoulli(50, 1 + I): float(exact);
bernoulli(50, float(1 + I))
DIGITS := 40: bernoulli(50, float(1 + I))
delete exact, DIGITS:
Некоторые системные функции, такие как diff или expand обработайте символьные вызовы bernoulli:
Некоторые системные функции, такие как diff или expand обработайте символьные вызовы bernoulli:
diff(bernoulli(n, f(x)), x)
expand(bernoulli(n, x + 2))
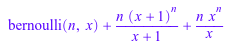
expand(bernoulli(n, -x))
expand(bernoulli(n, 3*x))
|
Арифметическое выражение, представляющее неотрицательное целое число |
|
Арифметическое выражение.
М. Абрамовиц и я. Stegun, “Руководство математических функций”, Dover Publications Inc., Нью-Йорк (1965).