Dom::MatrixGroupАбелева группа матриц
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Dom::MatrixGroup(m,n, <R>)
Dom::MatrixGroup(m, n, R)(Array)Dom::MatrixGroup(m, n, R)(Matrix)Dom::MatrixGroup(m, n, R)(<m, n>)Dom::MatrixGroup(m, n, R)(<m, n>,List)
Dom::MatrixGroup(m, n, R)(<m, n>,ListOfRows)
Dom::MatrixGroup(m, n, R)(<m, n>,f)
Dom::MatrixGroup(m, n, R)(<m, n>,List, <Diagonal>)
Dom::MatrixGroup(m, n, R)(<m, n>,g, <Diagonal>)
Dom::MatrixGroup(m, n, R)(<m, n>,List, <Banded>)
Dom::MatrixGroup(m, n, R) создает область, которая представляет Абелевую группу m ×n матрицы по кольцевому R компонента, т.е. это - область категории Cat::AbelianGroup.
Доменный Dom::ExpressionField() используется в качестве звонка компонента для матриц если дополнительный параметр R не дан.
Для матриц области, созданной Dom::MatrixGroup(m, n, R), матричная арифметика реализована путем перегрузки стандартных арифметических операторов +, -, *, / и ^. Могут быть применены все функции linalg пакета, имеющего дело с матрицами.
Dom::MatrixGroup(m, n, R) имеет доменный Dom::Matrix(R) как его супер область, т.е. это наследовало каждый метод, который задан Dom::Matrix(R) и не повторно реализованный Dom::MatrixGroup(m, n, R).
Методы, описанные ниже, реализованы Dom::MatrixGroup.
Доменный Dom::Matrix(R) представляет матрицы по R из произвольного размера, и это поэтому не имеет никакой алгебраической структуры (кроме того, чтобы быть набором матриц).
Доменный Dom::SquareMatrix(n, R) представляет звонок n ×n матрицы по R.
Dom::MatrixGroup(m, n, R)(Array) и Dom::MatrixGroup(m, n, R)(Matrix) создайте новую матрицу, сформированную записями Array и Matrix, соответственно.
Компоненты Array и Matrix, соответственно, преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Вызов Dom::MatrixGroup(m, n, R)( m , n ) возвращает m ×n нулевая матрица. Обратите внимание на то, что m ×n нулевая матрица может также быть найден в записи "zero" (см. ниже).
Dom::MatrixGroup(m, n, R)( m , n List) создает m ×n матрица с компонентами, взятыми из list List.
Этот вызов только позволен для m ×1 или 1 ×n матрица, т.е. если любой m или n равно одному.
Если список имеет слишком мало записей, остающиеся компоненты матрицы обнуляются.
Записи списка преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::MatrixGroup(m, n, R)( m , n ListOfRows) создает m ×n матрица с компонентами, взятыми из вложенного list ListOfRows. Каждый внутренний список соответствует строке матрицы.
Если внутренний список имеет меньше, чем n записи, остающиеся компоненты в соответствующей строке матрицы обнуляются. Если там меньше m внутренние списки, остающиеся более низкие строки матрицы заполнены, обнуляет.
Записи внутренних списков принуждены в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Это может быть хорошая идея сначала, чтобы создать двумерный массив из того списка прежде, чем вызвать Dom::MatrixGroup(m, n, R). Это - то, вследствие того, что создание матрицы от массива является самым быстрым способом, которым можно достигнуть. Однако в этом случае подсписки должны иметь то же число элементов.
Dom::MatrixGroup(m, n, R)( m , n f) возвращает матрицу, чья (i, j) th компонент значение вызова функции f(i, j). Индекс строки i лежит в диапазоне от 1 до m и индекс столбца j от 1 до n.
Значения функции принуждены в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::Matrix(R)
Если R имеет Ax::canonicalRep, затем Ax::canonicalRep.
Много примеров может быть найдено на странице справки доменного конструктора Dom::Matrix, и большинство из них является также примерами для работы с областями, созданными Dom::MatrixGroup. Этот пример только подсвечивает некоторые различия относительно работы с матрицами доменного Dom::Matrix(R).
Следующая команда задает абелевую группу 3 ×4 матриц по rationals:
MatGQ := Dom::MatrixGroup(3, 4, Dom::Rational)
MatGQ::hasProp(Cat::AbelianGroup), MatGQ::hasProp(Cat::Ring)
MatGQ коммутативная группа относительно сложения матриц. Модуль этой группы является 3 нулевыми матрицами ×4:
MatGQ::zero
Обратите внимание на то, что некоторые операции заданы доменным MatGQ возвратите матрицы, которые больше не являются элементами матричной группы. Они возвращают матрицы доменного Dom::Matrix(Dom::Rational), суперобласть MatGQ.
Например, если мы задаем матрицу:
A := MatGQ([[1, 2, 1, 2], [-5, 3], [2, 1/3, 0, 1]])
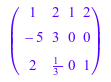
и удалите его третий столбец, мы получаем матрицу:
MatGQ::delCol(A, 3)
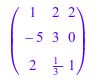
который имеет доменный тип:
domtype(%)
Как другой пример мы создаем 3×3 единичная матрица с помощью метода "identity" из нашей области:
E3 := MatGQ::identity(3)
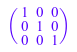
Это - также матрица доменного Dom::Matrix(Dom::Rational):
domtype(E3)
Если мы конкатенируем E3 справа от матричного A заданный выше, мы получаем 3 ×7 матрицы:
B := A . E3
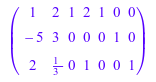
который имеет доменный тип Dom::Matrix(Dom::Rational):
domtype(B)
Мы можем преобразовать матрицу от области, созданной с Dom::MatrixGroup в или от другой матричной области, как показано затем:
MatGR := Dom::MatrixGroup(2, 3, Dom::Real): MatC := Dom::Matrix(Dom::Complex):
A := MatGR((i, j) -> i*j)
Преобразовывать A в матрицу доменного MatC, Введите:
coerce(A, MatC)
domtype(%)
Преобразование сделано покомпонентно. Например, мы задаем следующую матрицу:
B := MatC([[0, 1, 0], [exp(I), 0, 1]])
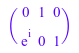
Матричный B имеет один комплексный компонент и поэтому не может быть преобразован в доменный MatGR:
coerce(B, MatGR)
Примечание: системная функция coerce использует методы "convert" и "convert_to" реализованный любой областью создается с Dom::MatrixGroup и Dom::Matrix.
|
Положительные целые числа (матричная размерность) |
|
Коммутативный звонок, т.е. область категории |
|
m ×n массив |
|
m ×n матрица, т.е. элемент области категории |
|
Список матричных компонентов |
|
Список в большей части |
|
Функция или функциональное выражение двумя параметрами (индекс строки и столбца) |
|
Функция или функциональное выражение одним параметром (индекс строки) |
|
Создайте диагональную матрицу С опцией
Записи
Значения функции принуждены в элементы доменного |
|
Создайте полосную матрицу Теплица С опцией Ленточная матрица имеет весь нуль записей вне основной диагонали и некоторые смежные под - и супердиагоналей.
Все элементы основной диагонали созданной матрицы инициализируются со средним элементом Записи |
| "один" | только задан если |
| "randomDimen" | установлен в |
| "нуль" | m ×n нулевая матрица. |
evalp — Оценка матриц полиномов в определенный моментevalp(A, x = a, …)
Этот метод только задан если R полиномиальный звонок категории Cat::Polynomial.
Этот метод перегружает функциональный evalp для матриц, т.е. можно использовать его в форме evalp(A, x = a).
identity Единичная матрицаidentity(k)
Возвращенная матрица имеет доменный Dom::Matrix(R), если
или если
.
matdim — Матричная размерностьmatdim(A)
random — Случайная генерация матрицыrandom()
Компоненты случайной матрицы случайным образом сгенерированы с методом "random" из кольцевого R компонента.
_concat — Горизонтально конкатенация матриц_concat(A, B, …)
Сообщение об ошибке выпущено, если данные матрицы не имеют одинакового числа строк.
Возвращенная матрица имеет доменный Dom::Matrix(R).
Этот метод перегружает функциональный _concat для матриц, т.е. можно использовать его в форме A . B . ..., или в функциональном обозначении: _concat(A, B, ...).
_index Индексирование матриц_index(A, i, j)
_index(A, r1 .. r2, c1
.. c2)
_index(A, i)
_index(A, i1 .. i2)
Если i и j не целые числа, затем вызов этого метода возвращается в его символьной форме (типа "_index") с оцененными аргументами.
В противном случае сообщение об ошибке дано, если i и j не допустимые индексы строки и столбца, соответственно.
Обратите внимание на то, что системная функция context используется, чтобы оценить запись в контексте среды вызова.
Этот метод перегружает функциональный _index для матриц, т.е. можно использовать его в форме A[i, j] или в функциональном обозначении: _index(A, i, j).
Возвращает субматрицу A, созданный строками A с индексами от r1 к r2 и столбцы A с индексами от c1 к c2.
Субматрица имеет доменный Dom::Matrix(R).
Этот метод возвращает i th запись A.
Если i не целое число, затем вызов этого метода возвращается в его символьной форме (типа "_index") с оцененными аргументами.
В противном случае сообщение об ошибке дано, если i меньше один или больше, чем размерность v.
Этот вызов только допускается 1×n или m ×1 матрицы, т.е. любой m или n должно быть равно одному. В противном случае сообщение об ошибке выпущено.
Обратите внимание на то, что системная функция context используется, чтобы оценить запись в контексте среды вызова.
Этот метод возвращает подвектор A, сформированный записями с индексом i1 к i2 (см. также метод "op").
Этот вызов только допускается 1×n или m ×1 матрицы, т.е. любой m или n должно быть равно одному. В противном случае сообщение об ошибке выпущено.
Этот метод перегружает функциональный _index для матриц, т.е. можно использовать его в форме A[i,j], A[r1..r2,c1..c2], A[i] или A[i1..i2], соответственно, или в функциональном обозначении: _index(A, ...).
concatMatrix — Горизонтально конкатенация матрицconcatMatrix(A, B,
…)
col — Извлечение столбцаcol(A, c)
Сообщение об ошибке выпущено если c меньше один или больше, чем n.
delCol — Удаление столбцаdelCol(A, c)
NIL возвращен если A только состоит из одного столбца.
Возвращенная матрица имеет доменный Dom::Matrix(R).
Сообщение об ошибке выпущено если c меньше один или больше, чем n.
delRow — Удаление строкиdelRow(A, r)
NIL возвращен если A только состоит из одной строки.
Возвращенная матрица имеет доменный Dom::Matrix(R).
Сообщение об ошибке выпущено если r меньше один или больше, чем m.
row — Извлечение строкиrow(A, r)
Сообщение об ошибке выпущено если r меньше один или больше, чем m.
stackMatrix — Конкатенация матриц вертикальноstackMatrix(A, B, …)
Сообщение об ошибке выпущено, если данные матрицы не имеют одинакового числа столбцов.
Возвращенная матрица имеет доменный Dom::Matrix(R).
convert — Преобразование в матрицуconvert(x)
FAIL возвращен, если преобразование перестало работать.
x май или быть m ×n массив или m ×n матрица категории Cat::Matrix.
x может также быть список. Смотрите параметр List и ListOfRows в “Создании Элементов” выше для допустимых значений x.
Записи x должно быть конвертируемо в элементы доменного R, в противном случае FAIL возвращен.