`Dom`::`Matrix`

Матрицы

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

Доменное создание

Dom::Matrix(<R>)

Создание элемента

Dom::Matrix(R)(Array)

Dom::Matrix(R)(List)

Dom::Matrix(R)(ListOfRows)

Dom::Matrix(R)(Matrix)

Dom::Matrix(R)(m, n)

Dom::Matrix(R)(m, n, Array)

Dom::Matrix(R)(m, n, List)

Dom::Matrix(R)(m, n, ListOfRows)

Dom::Matrix(R)(m, n, Table)

Dom::Matrix(R)(m, n, [(i₁, j₁) = value₁, (i₂, j₂) = value₂, …])

Dom::Matrix(R)(m, n, f)

Dom::Matrix(R)(m, n, List, Diagonal)

Dom::Matrix(R)(m, n, g, Diagonal)

Dom::Matrix(R)(m, n, List, Banded)

Dom::Matrix(R)(1, n, Array)

Dom::Matrix(R)(1, n, List)

Dom::Matrix(R)(1, n, Table)

Dom::Matrix(R)(1, n, [j₁ = value₁, j₂ = value₂, …])

Dom::Matrix(R)(m, 1, Array)

Dom::Matrix(R)(m, 1, List)

Dom::Matrix(R)(m, 1, Table)

Dom::Matrix(R)(m, 1, [i₁ = value₁, i₂ = value₂, …])

Описание

Доменное создание

Dom::Matrix(R) создает области матриц по доменному R компонента из категории Cat::Rng (звонок, возможно без модуля).

Если дополнительный параметр R не дан, Dom::ExpressionField() используется в качестве области компонента. Матрицы этого типа принимают произвольные выражения MuPAD^® (числа, символы и т.д.) как записи. Имя matrix псевдоним для этого матричного доменного Dom::Matrix() по умолчанию.

Вектором с записями n является любой n ×1 матрица (вектор-столбец), или 1×n матрица (вектор-строка).

Арифметические операции с матрицами могут быть выполнены при помощи стандартных арифметических операторов MuPAD.

Например, если A и B две матрицы, заданные Dom::Matrix(R), A + B вычисляет сумму и A * B вычисляет продукт этих двух матриц, при условии, что размерности являются соответствующими.

Точно так же A^(-1) или 1/A вычисляет инверсию квадратной матрицы A если это существует. В противном случае, FAIL возвращен. Смотрите Пример 1.

Много системных функций перегружаются для матриц, таких как map, subs, haszip, Например, используйте conjugate вычислить сопряженное комплексное число матрицы, norm вычислить матричные нормы или exp вычислить экспоненциал матрицы.

Большинство функций в пакете линейной алгебры MuPAD linalg работает с матрицами. Например, команда linalg::gaussJordan(A) выполняет Исключение по Гауссу-Жордану на A преобразовать A к его приведенному ступенчатому по строкам виду матрицы.

См. документацию linalg для списка доступных функций этого пакета.

Доменный Dom::Matrix(R) представляет матрицы по R из произвольного размера. Поэтому это не имеет никакой алгебраической структуры (кроме того, чтобы быть набором матриц).

В этой странице справки мы используем следующие обозначения в матричном A (элемент Dom::Matrix(R)):

nrows (A) обозначает количество строк A.
ncols (A) обозначает количество столбцов A.
Индекс строки является целым числом в диапазоне от 1 до nrows (A).
Индекс столбца является целым числом в диапазоне от 1 до ncols (A).

Примечание

Количество строк и столбцов, соответственно, матрицы должно быть меньше ²³¹.

Примечание

Компоненты матрицы больше не оцениваются после создания матрицы, т.е. если они содержат свободные идентификаторы, они не будут заменены их значениями.

Создание элемента

Dom::Matrix(R)(Array) и Dom::Matrix(R)(Matrix) создайте новую матрицу с размерностью и компонентами Array и Matrix, соответственно.

Компоненты Array или Matrix преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Создание (разреженных) матриц через массивы полезно для матриц умеренного размера. Обратите внимание на то, что индексируемые присвоения на массивы намного быстрее, чем соответствующие индексируемые присвоения на матрицы. Однако, поскольку все элементы массива (включая обнуление) должны быть заполнены в том, прежде чем преобразование в (разреженную) матрицу, память будет потрачена впустую для очень большого и очень разреженных матриц. В такой ситуации нужно задать таблицу, содержащую только ненулевые элементы, и преобразовать таблицу в матрицу (см. ниже).

Dom::Matrix(R)(List) создает m ×1 вектор-столбец с компонентами, взятыми из непустого списка, где m является количеством записей List.

Можно также использовать список уравнений, чтобы создать объект Dom::Matrix. В этом случае записи списка должны иметь форму (i, j) = value, где i и j обозначьте индекс строки и столбца и value коэффициент матрицы. i и j должны быть положительные целые числа.

Dom::Matrix(R)(ListOfRows) создает m ×n матрица с компонентами, взятыми из вложенного списка ListOfRows, где m является количеством внутренних списков ListOfRows, и n является максимальным числом элементов внутреннего списка. Каждый внутренний список соответствует строке матрицы. И m и n должны быть ненулевыми.

Если внутренний список имеет меньше, чем записи n, остающиеся компоненты в соответствующей строке матрицы обнуляются.

Записи внутренних списков преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Вызов Dom::Matrix(R)(m, n) возвращает m ×n нулевая матрица.

Используйте метод "identity" создать n ×n единичная матрица.

Вызов Dom::Matrix(R)(m, n, Array) создает m ×n матрица с компонентами, взятыми из Array, который должен быть массивом или hfarray. Array должен иметь m n операнды. Первые операнды m задают первую строку, следующие операнды m задают вторую строку и т.д. Форматирование массива не важно. Например, любой массив с 6 элементами может использоваться, чтобы создать матрицу размерности 1 ×6, или 2×3, или 3×2, или 6 ×1.

Dom::Matrix(R)(m, n, List) создает m ×n матрица с компонентами взятая строка после строки из непустого списка. Список должен содержать m n записи.

Dom::Matrix(R)(m, n, ListOfRows) создает m ×n матрица с компонентами, взятыми из списка ListOfRows.

Если m ≥ 2 и n ≥ 2, то ListOfRows должен состоять из в большей части m внутренние списки, каждый имеющий в большей части n записи. Внутренние списки соответствуют строкам возвращенной матрицы.

Если внутренний список имеет меньше, чем n записи, остающиеся компоненты соответствующей строки матрицы обнуляются. Если там меньше m внутренние списки, остающиеся более низкие строки матрицы заполнены, обнуляет.

Dom::Matrix(R)(m, n, Table) создает m ×n матрица с компонентами, взятыми из таблицы Table.

Путем определения записей таблицы сначала, можно легко создать большой и разреженные матрицы. Запись Table[i, j] из таблицы будет запись в i- строка th и j- столбец th матрицы. Поэтому таблица должна быть индексирована положительными целыми числами i и j.

Dom::Matrix(R)(m, n, [(i1, j1) = value1, (i2, j2) = value2, ...]) дальнейший путь состоит в том, чтобы создать матрицу, задающую только ненулевые записи A[i1, j1] = value1, A[i2, j2] = value2 и т.д. Упорядоченное расположение записей в списке входов не важно.

Dom::Matrix(R)(m, n, f) возвращает матрицу, чья (i, j)-th компонент значение вызова функции f(i, j). Индекс строки i лежит в диапазоне от 1 до m и индекса столбца j от 1 до n.

Значения функции преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Dom::Matrix(R)(1, n, Array) возвращает 1 ×n вектор-строку с компонентами, взятыми из Array. array или hfarray Array должен иметь n записи.

Записи массива преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Dom::Matrix(R)(1, n, List) возвращает 1 ×n вектор-строку с компонентами, взятыми из List. Список List должен иметь в большей части n записи. Если существует меньше записей, остающиеся векторные компоненты обнуляются.

Записи списка преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Dom::Matrix(R)(1, n, Table) возвращает 1 ×n вектор-строку с компонентами, взятыми из Table. Таблица Table не должен иметь больше, чем n записи. Если существует меньше записей, остающиеся векторные компоненты рассматриваются как нуль.

Dom::Matrix(R)(m, 1, Array) возвращает m ×1 вектор-столбец с компонентами, взятыми из Array. array или hfarray Array должен иметь m записи.

Dom::Matrix(R)(m, 1, List) возвращает m ×1 вектор-столбец с компонентами, взятыми из List. Список List должен иметь в большей части m записи. Если существует меньше записей, остающиеся векторные компоненты обнуляются.

Dom::Matrix(R)(m, 1, Table) возвращает m ×1 вектор-столбец с компонентами, взятыми из Table. Таблица Table должен иметь не больше, чем m записи. Если существует меньше записей, остающиеся векторные компоненты рассматриваются как нуль.

Суперобласть

Dom::BaseDomain

Аксиомы

Если R имеет Ax::canonicalRep, затем Ax::canonicalRep.

Категории

Cat::Matrix(R)

Примеры

Пример 1

Каждый раз, когда возможно, нужно использовать Dom::ExpressionField() как содействующая область матриц – поэтому Dom::ExpressionField() содействующая область по умолчанию матриц.

Компоненты матриц по Dom::ExpressionField() могут быть произвольные арифметические выражения. Рассмотреть

Mat := Dom::Matrix()

Мы присвоили область идентификатору Mat и теперь мы можем задать матричный A двух строк, где каждая строка является списком двух элементов следующей линией:

A := Mat([[1, 5], [2, 3]])

Таким же образом мы задаем следующие 2 ×3 матрицы:

B := Mat([[-1, 5/2, 3], [1/3, 0, 2/5]])

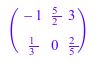
и выполните матричную арифметику с помощью стандартных арифметических операторов MuPAD, например, матричное произведение A B, четвертая степень A, а также скалярное умножение времен A:

A * B, A ^ 4, 1/3 * A

Матрицы A и B имеют различные размерности, и поэтому сумму A и B, не заданы. MuPAD выдает ошибку сообщение:

A + B

Error: Dimensions do not match. [(Dom::Matrix(Dom::ExpressionField()))::_plus]

Чтобы вычислить инверсию A, только войдите:

1/A

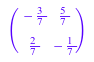
Если матрица не является обратимой, FAIL результат этой операции. Например, матрица:

C := Mat(2, 2, [[2]])

не является обратимым, следовательно:

C^(-1)

delete A, B, C:

Пример 2

Мы создаем область матриц по звонку coeffcient Dom::ExpressionField():

Mat := Dom::Matrix()

Около стандартной матричной арифметики библиотека linalg предлагает много функций, имеющих дело с матрицами. Например, если вы хотите вычислить ранг матрицы, используйте linalg::rank:

A := Mat([[1, 2], [2, 4]])

linalg::rank(A)

Используйте linalg::eigenvectors вычислить собственные значения и собственные вектора матричного A:

linalg::eigenvectors(A)

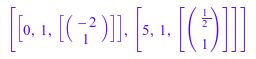
Попробуйте info(linalg) для списка доступных функций, или вводят help(linalg) для получения дополнительной информации о библиотеке linalg.

Некоторые функции в linalg пакет просто служит “интерфейсными” функциями для методов матричной области, описанной выше. Например, linalg::transpose использует метод "transpose" получить транспонированную матрицу. Функциональный linalg::gaussElim применяет Исключение Гаусса к матрице путем вызова метода "gaussElim":

linalg::gaussElim(A) = A::dom::gaussElim(A)[1]

В отличие от методов доменного Dom::Matrix(R), соответствующие функции linalg пакеты делают расширенную проверку своих входных параметров. Обратите внимание на то, что могут быть незначительные различия в функциональности linalg функции и матричные методы. Например, опция ColumnElimination не доступно в linalg::gaussElim, но только в "gaussElim" метод матричной области:

A::dom::gaussElim(A, ColumnElimination)

delete A:

Пример 3

Мы создаем матричный доменный Dom::Matrix() по умолчанию. Как ярлык, эта область может также быть создана через matrix:

A := matrix([[ 1, 2, 3, 4], 
                   [ 2, 0, 4, 1], 
                   [-1, 0, 5, 2]])

domtype(A)

Матричные компоненты могут быть извлечены оператором индекса []:

A[2, 1] * A[1, 2] - A[3, 1] * A[1, 3]

Если один из индексов не находится в его допустимой области значений, сообщение об ошибке выпущено. Присвоения на матричные компоненты выполняются так же:

delete a:
A[1, 2] := a^2: A

Около обычной индексации матричных компонентов также возможно извлечь подматрицы из данной матрицы. Следующий вызов создает субматрицу A, который состоит из строк 2 - 3 и столбцов 1 - 3 A:

A[2..3, 1..3]

Оператор индекса не позволяет вставлять подматрицы в данную матрицу. Это реализовано функциональным linalg::substitute.

delete A:

Пример 4

В следующих примерах мы демонстрируем различные способы создать матрицы. Мы работаем с матрицами, заданными по полю ℤ₁₉, т.е. полю целых чисел по модулю 19. Этот звонок компонента может быть создан с доменным конструктором Dom::IntegerMod.

Мы запускаем путем предоставления списка строк, где каждая строка является списком записей строки:

MatZ19 := Dom::Matrix(Dom::IntegerMod(19)):
MatZ19([[1, 2], [2]])

Элементы двух внутренних списков, записей строки, были преобразованы в элементы доменного Dom::IntegerMod(19).

Количество строк является количеством подсписков аргумента, т.е. m = 2. Количество столбцов определяется длиной внутреннего списка с большинством записей, который является первым внутренним списком с двумя записями. Недостающие записи в других внутренних списках обработаны как нулевые компоненты. Вызов:

MatZ19(4, 4, [[1, 2], [2]])

фиксирует размерность матрицы. Недостающие записи и внутренние списки обработаны как нулевые компоненты и обнуляют строки, соответственно.

Сообщение об ошибке выпущено, если одна из данных записей не может быть преобразована в элемент по ℤ ₁₉:

MatZ19([[2, 3], [-1, I]])

Error: Unable to define a matrix over 'Dom::IntegerMod(19)'. [(Dom::Matrix(Dom::IntegerMod(19)))::new]

delete MatZ19:

Пример 5

Этот пример иллюстрирует, как создать матрицу с компонентами, данными как значения функции индекса. Сначала мы создаем 2 ×2 Гильбертовых матрицы (см. также функции linalg::hilbert и linalg::invhilbert):

Dom::Matrix()(2, 2, (i, j) -> 1/(i + j - 1))

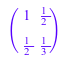
Отметьте различие при работе с выражениями и функциями. Если вы даете выражение, оно обработано как функция в индексах строки и столбца:

delete x:
Dom::Matrix()(2, 2, x), Dom::Matrix()(2, 2, (i, j) -> x)

Пример 6

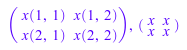
Диагональные матрицы могут быть созданы с опцией Diagonal и список диагональных компонентов:

Mat := Dom::Matrix():
Mat(3, 4, [1, 2, 3], Diagonal)

Следовательно, чтобы задать n ×n единичная матрица, можно войти:

Mat(3, 3, [1 $ 3], Diagonal)

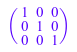
или вызов:

Mat(3, 3, x -> 1, Diagonal)

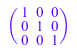
Самый легкий способ создать единичную матрицу, однако, состоит в том, чтобы использовать метод "identity":

Mat::identity(3)

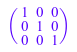
delete Mat:

Пример 7

Матрицы Теплица могут быть заданы с опцией Banded. Следующий вызов задает три ленточных матрицы с 2 компонента на основной диагонали и компоненте - 1 на первой поддиагонали и супердиагонали:

Dom::Matrix()(4, 4, [-1, 2, -1], Banded)

Пример 8

Некоторые системные функции могут быть применены к матрицам, таким как normрасширениеdiff, conjugate, или exp.

Например, чтобы расширить компоненты матрицы:

delete a, b: 
A := Dom::Matrix()(
  [[(a - b)^2, a^2 + b^2], [a^2 + b^2, (a - b)*(a + b)]]
)

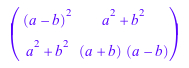
войдите:

expand(A)

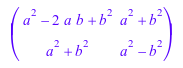
Если вы хотите дифференцировать матричные компоненты, то вызовите, например:

diff(A, a)

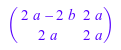
Заменять матричными компонентами некоторыми значениями, введите:

subs(A, a = 1, b = -1)

Функциональный zip может также быть применен к матрицам. Следующий вызов комбинирует две матрицы A и B путем деления каждого компонента A соответствующим компонентом B:

A := Dom::Matrix()([[4, 2], [9, 3]]): 
B := Dom::Matrix()([[2, 1], [3,-1]]):
zip(A, B, `/`)

Заключенный в кавычки символьный `/` другое обозначение для функционального _divide, функциональная форма оператора деления /.

Если нужно применить функцию к компонентам матрицы, то используйте функциональный map. Например, чтобы упростить компоненты матрицы:

C := Dom::Matrix()(
  [[sin(x)^2 + cos(x)^2, cos(x)*tan(x)], 
  [(a^2 - b^2)/(a + b), 1]]
)

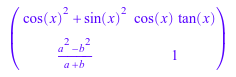
вызов:

map(C, Simplify)

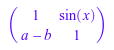
delete A, B, C:

Пример 9

Однако там может появиться некоторые неожиданные результаты с помощью функционального diff в контексте матриц. Производная следующего незаданного функционального f из матрицы вычисляется из-за цепочечного правила:

diff(f(matrix([[a*x^2, b], [c, d]])), x)

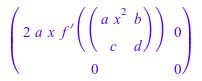
Обычно, функциональный f был бы неявно принят, чтобы быть скаляром. Следовательно, производная f должен быть скаляр также. В вышеупомянутой ситуации цепочечное правило применяется для дифференцирования: внутренняя функция является матрицей, содержащей символьные компоненты a*x^2BC и d. Его производная вычисляется путем простого применения diff к каждому компоненту матрицы:

diff(matrix([[a*x^2, b], [c, d]]), x)

Наконец, внешний незаданный функциональный f неявно принят, чтобы быть скаляром, таким, что каждый компонент производной внутренней функции умножается на внешнее дифференцирование.

Пример 10

Вектор-столбец представлен 2×1 матрица:

Mat := Dom::Matrix():
v := Mat(2, 1, [1, 2])

Размерность этого вектора:

Mat::matdim(v)

Длина вектора может также быть запрошена linalg::vecdim или nops(v):

linalg::vecdim(v)

i th компонент этого вектора может быть извлечен двумя способами: любой v[i, 1] или v[i]:

v[1], v[2]

Мы вычисляем 2-норму v следующим вызовом:

norm(v, 2)

delete Mat, v:

Пример 11

Мы создаем случайные матрицы по полю рациональных чисел. Рассмотрите случайный матричный A1 с 3 строками и 3 столбцами:

Mat := Dom::Matrix(Dom::Rational):
A1 := Mat::random(3, 3)

Второй матричный A2 должен содержать самое большее 2 ненулевых записи. Мы можем создать такую матрицу при помощи 2 в качестве третьего аргумента для random:

A2 := Mat::random(3, 3, 2)

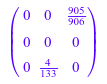
Продуктом этих матриц дают

C := A1 * A2

По умолчанию матрицы отображены как 'плотные' массивы с, обнуляет в пустых местах. Для разреженных матриц большого столбца и/или размерности строки, такой 'плотный' режим печати не является соответствующим: форматирование печати выход было бы очень трудоемким. Далее, 'плотная' печать выход не очень информативна для разреженных матриц. Поэтому "doprint" метод обеспечивает разреженный режим вывода, распечатывающий только ненулевые записи:

C::dom::doprint(C)

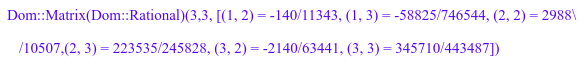
С этим методом можно также распечатать большие разреженные матрицы. Мы создаем случайную разреженную матрицу с 100 строками, 200 столбцами и самое большее 6 ненулевыми записями:

X := Mat::random(100, 200, 6):  print(X)

Warning: Matrix too large for display. To see all nonzero entries of a matrix A, use 'A::dom::doprint(A)'. [(Dom::Matrix(Dom::Rational))::print]

Предупреждение выступает за себя. X рассматривается как 'слишком большой для отображения' с тех пор, с 'плотным' режимом вывода по умолчанию, разреженная матрица была бы распечатана, когда огромная подобная массиву структура размерности 100×200 с (целым числом) обнуляет в пустых местах. Разреженный режим печати должен использоваться:

X::dom::doprint(X)

Для удобства существует функциональный doprint это вызывает этот метод, только войдя:

doprint(X)

delete Mat, A1, A2, C, X:

Параметры

`R`	Звонок, т.е. область категории `Cat::Rng`. Звонком по умолчанию является `Dom::ExpressionField()`.
`Array`	Один - или двумерный `array` или `hfarray`
`Matrix`	Матрица A, т.е. элемент области категории `Cat::Matrix`
`mN`	Матричная размерность (положительные целые числа)
`List`	Список матричных компонентов
`ListOfRows`	Список в большей части `m` 'Строки' ; каждая строка, данная как список в большей части `n` матричные компоненты
`Table`	Таблица коэффициентов матрицы для разреженного входа
`f`	Функция или функциональное выражение двумя параметрами (индекс строки и столбца)
`g`	Функция или функциональное выражение одним параметром (индекс строки)

Опции

Diagonal

Создайте диагональную матрицу

С опцией Diagonal, диагональные матрицы могут быть созданы с диагональными элементами, взятыми из списка, или вычислили функцией или функциональным выражением.

Dom::Matrix(R)(m, n, List, Diagonal) создает m ×n диагональная матрица, диагональные элементы которой являются записями List.

List должен иметь в большей части min (m, n) записи. Если это имеет меньше элементов, остающиеся диагональные элементы обнуляются.

Записи List преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.

Dom::Matrix(R)(m, n, g, Diagonal) возвращает разреженную матрицу, i которой th диагональный элемент является g(i, i), куда индекс i запускается от 1 до min (m, n).

Banded

Создайте матрицу Теплица

Dom::Matrix(R)(m, n, List, Banded) создает m ×n матрица Теплица с элементами List как записи. Количество записей List должно быть нечетным, сказать 2 h + 1 и не должен превышать 2 min (m, n) - 1. Пропускная способность получившейся матрицы самое большее 2 h + 1.

Матрица Теплица является матрицей, где элементы каждой полосы идентичны. См. также Пример 7.

Все элементы основной диагонали созданной матрицы инициализируются со средним элементом List. Все элементы i-th поддиагональ инициализируются с (h + 1 - i)-th элемент List. Все элементы i-th супердиагональ инициализируются с (h + 1 + i)-th элемент List. Все записи на остающемся под - и супердиагонали обнуляются.

Записи

issparse	`всегда TRUE`.
"randomDimen"	установлен в `[10, 10]`. См. метод `"random"` ниже для деталей.

Методы

развернуть все

Математические методы

`_divide` — Разделите матрицы

_divide(A, B)

Сообщение об ошибке выпущено если размерности A и B не соответствовать.

Этот метод только существует если R коммутативный звонок с модулем, т.е. область категории Cat::Ring.

Этот метод перегружает системную функцию _divide для матриц, т.е. можно использовать его в форме A / B, или в функциональном обозначении: _divide(A, B).

`_invert` — Вычислите инверсию матрицы

_invert(A, Normal = b)

Этот метод только существует если R область категории Cat::Ring.

Этот метод перегружает системную функцию _invert для матриц, т.е. можно использовать его в форме 1/A или A^(-1), или в функциональном обозначении: _invert(A).

Если Normal = TRUE, затем обратная матрица всегда возвращается в нормированной форме. Для получения дополнительной информации о нормализации, смотрите normal. Если Normal = FALSE, затем обратная матрица может появиться в нормированной форме, но нормализация не гарантируется. Normal = TRUE по умолчанию.

Normal влияет на результаты, только если матрица содержит переменные или точные выражения, такие как sqrt(5) или sin(PI/7).

`_mod` — Сопоставьте оператор по модулю с элементами матрицы

_mod(A, n)

n должно быть ненулевым, и a mod n должен быть задан для каждой записи a из A.

Этот метод перегружает функциональный _mod для матриц; можно использовать его в форме A mod n, или в функциональном обозначении: _mod(A, n).

`_mult` — Матрицы мультиплие матрицами, векторами и скалярами

_mult(x, y)

Если y имеет доменный тип R или может быть преобразован в такой элемент, соответствующее скалярное умножение вычисляется.

В противном случае, y преобразован в матрицу доменного типа x. Если это преобразование перестало работать, это вызовы метода метод "_mult" из области y предоставление всех аргументов в том же порядке.

Если x матрица того же доменного типа как y, матричное произведение x y вычисляется. Сообщение об ошибке выпущено, если размерности матриц не соответствуют.

Если x имеет доменный тип R или может быть преобразован в такой элемент, соответствующее скалярное умножение вычисляется.

В противном случае, x преобразован в матрицу доменного типа y. Если это преобразование перестало работать, FAIL возвращен.

Этот метод обрабатывает больше чем два аргумента путем вызова себя рекурсивно с первой половиной всех аргументов и последней половиной всех аргументов. Затем продукт этих двух результатов вычисляется с системной функцией _mult.

Этот метод перегружает системную функцию _mult для матриц, т.е. можно использовать его в форме x * y, или в функциональном обозначении: _mult(x, y).

`_negate` — Инвертируйте матрицу

_negate(A)

Этот метод перегружает системную функцию _negate для матриц, т.е. можно использовать его в форме -A, или в функциональном обозначении: _negate(A).

`_plus` — Добавьте матрицы

_plus(A, B, …)

Аргументы A, B , ... преобразованы в матрицы доменного типа Dom::Matrix(R). FAIL возвращен, если одно из этих преобразований перестало работать.

Этот метод перегружает системную функцию _plus для матриц, т.е. можно использовать его в форме A + B, или в функциональном обозначении: _plus(A, B).

`_power` — Целочисленная степень матрицы

_power(A, n)

Если степень n отрицательное целое число затем A должно быть несингулярным и R должна быть область категории Cat::IntegralDomain. В противном случае FAIL возвращен.

Если n нуль и кольцевой R компонента звонок без модуля (т.е. категории Cat::Rng, но не категории Cat::Ring), FAIL возвращен.

Этот метод перегружает системную функцию _power для матриц, т.е. можно использовать его в форме A^n, или в функциональном обозначении: _power(A, n).

`conjugate` — Сопряженное комплексное число матрицы

conjugate(A)

Этот метод только существует если R реализует метод "conjugate", который вычисляет сопряженное комплексное число элемента доменного R.

Этот метод перегружает системную функцию conjugate для матриц, т.е. можно использовать его в форме conjugate(A).

`cos` — Косинус матрицы

cos(A)

Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет расчет cos(elem) для произвольного элемента elem из звонка компонента, FAIL возвращен.

Этот метод использует функциональный numeric::expMatrix для приближения с плавающей точкой экспоненциала A если A задан по доменному Dom::Float.

Если некоторые собственные значения A не существуйте в R или не может быть вычислен, затем FAIL возвращен.

В символьном случае функции exp и linalg::jordanForm называются. Последний не может смочь вычислить Жорданову форму A. В этом случае FAIL возвращен.

Этот метод только существует если R область категории Cat::Field.

Этот метод перегружает функциональный cos для матриц, т.е. можно использовать его в форме cos(A).

`diff` — Дифференцирование матричных компонентов

diff(A, …)

Этот метод только существует если R реализует метод "diff".

Этот метод перегружает системную функцию diff для матриц, т.е. можно использовать его в форме diff(A, ...). Смотрите пример 8 и пример 9.

`equal` — Тест равенства матриц

equal(A, B)

Обратите внимание на то, что, если R имеет аксиому Ax::systemRep затем normal используется, чтобы упростить компоненты A и B прежде, чем протестировать их равенство.

`exp` — Экспоненциал матрицы

exp(A, <t>)

Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет расчет exp(elem) для произвольного элемента elem из звонка компонента, FAIL возвращен.

Этот метод использует функциональный numeric::expMatrix для приближения с плавающей точкой экспоненциала A если A*t содержит по крайней мере одно число с плавающей запятой, и все записи могут быть преобразованы в числа с плавающей запятой.

Если некоторые собственные значения A не существуйте в R или не может быть вычислен, затем FAIL возвращен.

В символьном случае, функциональном linalg::jordanForm называется, который не может смочь вычислить Жорданову форму A. В этом случае FAIL возвращен.

Этот метод только существует если R область категории Cat::Field.

Этот метод перегружает системную функцию exp для матриц, т.е. можно использовать его в форме exp(A, ...).

`expand` — Расширьте матричные компоненты

expand(A)

Этот метод только существует если R реализует метод "expand", или если R имеет аксиому Ax::systemRep (в этом случае, системная функция expand используется).

Этот метод перегружает системную функцию expand для матриц, т.е. можно использовать его в форме expand(A).

`factor` — Факторизация диагональной матрицы

factor(A)

Факторный s является GCD всех компонентов матричного A. Следовательно, этот метод только существует если R имеет категорию Cat::GcdDomain.

Этот метод перегружает системную функцию factor для матриц, т.е. можно использовать его в форме factor(A).

`float` — Приближение с плавающей точкой матричных компонентов

float(A)

Этот метод только существует если R реализует метод "float".

Примечание

Обычно приближения с плавающей точкой не являются элементами R!, Например, Dom::Integer реализует такой метод, но приближение с плавающей точкой целого числа не может быть повторно преобразовано в целое число.

Этот метод проверяет, может ли получившаяся матрица быть преобразована в доменный тип A только если testargs() возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).

В противном случае нужно заботиться, что возвращенная матрица совместима со своим звонком компонента.

`fourier` — Преобразование Фурье матричных компонентов

fourier(A, t, s)

Этот метод перегружает функциональный fourier для матриц.

`gaussElim` — Исключение Гаусса для матриц

gaussElim(A, <ColumnElimination>)

С опцией ColumnElimination, матричный A уменьшается до нижней треугольной формы эшелона через элементарные операции столбца (без ColumnElimination, алгоритм Гаусса использует элементарные операции строки, чтобы получить форму высшего руководства). Следующее отношение содержит: transpose(gaussElim(A, ColumnElimination)[1]) = gaussElim(transpose(A))[1]. С ColumnElimination, последняя запись возвращенного списка является набором характеристических индексов столбца A.

Для очень большого m ×n матрицы A с m намного больший n, устранение столбца быстрее, чем устранение строки.

Если матрица не является квадратной, т.е. определитель A не задан, затем третья запись возвращенного списка является значением FAIL.

Этот метод только существует если кольцевой R компонента интегральная область, т.е. область категории Cat::IntegralDomain.

Если R имеет метод "pivotSize", элемент центра самого маленького размера выбран на каждом вертящемся шаге, посредством чего pivotSize должен возвратить положительное целое число, представляющее “размер” элемента.

Если никакой такой метод не задан, Исключение Гаусса без стратегии центра применяется к A.

Если R имеет аксиому Ax::efficientOperation("_invert") и имеет категорию Cat::Field, обычное Исключение Гаусса используется. В противном случае устранение без частей выполняется на A.

Если R реализует метод "normal", это используется, чтобы упростить последующие расчеты процесса Исключения Гаусса.

Обратите внимание на то, что, если R не реализует метод "normal", но элементы R представлены областями ядра, т.е. R имеет аксиому Ax::systemRep, системная функция normal используется вместо этого.

`identity` Единичная матрица

identity(n)

Этот метод только существует если кольцевой R компонента имеет категорию Cat::Ring, т.е. звонок с модулем.

`int` — Интегрирование матричных компонентов

int(A, …)

Этот метод только существует если R реализует метод "int".

Этот метод перегружает системную функцию int для матриц, т.е. можно использовать его в форме int(A, ...).

`ifourier` — Обратное преобразование Фурье матричных компонентов

ifourier(A, s, t)

Этот метод перегружает функциональный ifourier для матриц.

`ilaplace` — Обратное Преобразование Лапласа матричных компонентов

ilaplace(A, s, t)

Этот метод перегружает функциональный ilaplace для матриц.

`iszero` — Протестируйте на нулевые матрицы

iszero(A)

Обратите внимание на то, что там может существовать больше чем одно представление нулевой матрицы данной размерности если R не имеет Ax::canonicalRep.

Если R реализует метод "normal", это используется, чтобы упростить компоненты A для нулевого теста.

Обратите внимание на то, что, если R не реализует такой метод, но элементы R представлены областями ядра, т.е. R имеет аксиому Ax::systemRep, системная функция normal используется вместо этого.

Этот метод перегружает системную функцию iszero для матриц, т.е. можно использовать его в форме iszero(A).

`laplace` — Преобразование Лапласа матричных компонентов

laplace(A, t, s)

Этот метод перегружает функциональный laplace для матриц.

`matdim` — Матричная размерность

matdim(A)

`norm` — Норма матриц и векторов

norm(A, Infinity)

norm(A, Maximum)

norm(v, Infinity)

norm(v, Maximum)

norm(A, Frobenius)

norm(A, 1)

norm(v, Euclidean)

norm(v, k)

norm(A, Maximum) вычисляет максимальную норму матричного A, который является максимальной суммой строки (сумма строки является суммой норм каждого компонента подряд).

Если доменный R не реализует методы "max" и "norm", FAIL возвращен.

Используя norm(v, Infinity) для векторного v максимальная норма всех элементов возвращена.

Если доменный R не реализует методы "max" и "norm", FAIL возвращен.

Используя norm(v, Maximum) для векторного v максимальная норма всех элементов возвращена.

Если доменный R не реализует методы "max" и "norm", FAIL возвращен.

norm(A, Frobenius) вычисляет норму Фробениуса A, который является квадратным корнем из суммы квадратов норм каждого компонента.

Если результатом больше не является элемент доменного R, или если R не реализует метод "norm", FAIL возвращен.

norm(A, 1) вычисляет 1 норму матричного A, который является максимальной суммой норм элементов каждого столбца. Если R не реализует методы "max" и "norm", FAIL возвращен.

norm(v, Euclidean) вычисляет Евклидову норму (2-норма) векторного v, который задан, чтобы быть квадратным корнем из суммы норм элементов v повышенный до квадрата.

FAIL возвращен, если результатом больше не является элемент доменного R. Функциональный linalg::scalarProduct используется для расчета Евклидова норма векторного v.

Если R не реализует метод "norm", FAIL возвращен.

norm(v, k) вычисляет k - норма векторного v, который задан, чтобы быть k th корень суммы норм элементов v повышенный до k th степень.

FAIL возвращен, если результатом больше не является элемент доменного R. Для k = 2, функциональный linalg::scalarProduct используется для расчета 2-норма v.

Если R не реализует метод "norm", FAIL возвращен.

Метод norm перегружает функциональный norm для матриц, т.е. можно использовать его в форме norm(A k ), где k любой Infinity, Frobenius, или положительное целое число. Значение по умолчанию k Infinity.

`normal` — Упрощение матричных компонентов

normal(A)

Если R не реализует метод "normal", но элементы R представлены областями ядра, т.е. R имеет аксиому Ax::systemRep, системная функция normal применяется к компонентам A. В противном случае normal(A) возвращает A без любых изменений.

Этот метод перегружает системную функцию normal для матриц, т.е. можно использовать его в форме normal(A).

`nonZeros` — Количество ненулевых компонентов матрицы

nonZeros(A)

`nonZeroes` — Количество ненулевых компонентов матрицы

nonZeroes(A)

`nonZeroOperands` — Возвратите последовательность всех ненулевых операндов

nonZeroOperands(A)

Этот метод полезен для получения информации о ненулевых записях. Например, чтобы узнать типы записей в матрице, не нужно считать все операнды op(A), потому что это также включило бы нулевые записи. Для больших матриц с немногими записями намного более эффективно использовать этот метод, чтобы извлечь записи.

`random` — Случайная генерация матрицы

random()

random(g)

random(m, n)

random(m, n, g)

random(m, n, p)

random(m, n, p, g)

Размерность матрицы также выбрана случайным образом. Матричный размер ограничивается значениями "randomDimen" (см. “Записи” выше). Изменить значение записи "randomDimen", нужно сначала оставить без защиты доменный Dom (см. unprotect для деталей).

При вызове "random" метод одним параметром g, этот параметр рассматривается как случайный генератор. Матричные записи создаются вызовами g() который должен возвратиться, элементы коэффициента звонят R.

Размерность матрицы выбрана случайным образом как выше.

При вызове "random" метод с двумя положительными целыми числами m и n, случайная матрица с m строки и n столбцы создаются. Его элементы сгенерированы методом "random" из кольцевого R компонента. Если R::random не существует, FAIL возвращен.

random(m,n,g) создает матрицу с m строки и n столбцы. Третий параметр g рассматривается как случайный генератор. Матричные записи создаются вызовами g() который должен возвратиться, элементы коэффициента звонят R.

При вызове "random" метод с положительными целыми числами mN и неотрицательный целочисленный p, разреженная матрица с m строки, n столбцы и в большей части p создаются ненулевые записи. Эти записи сгенерированы функциональным "random" из кольцевого R компонента. Если R::random не существует, FAIL возвращен.

Целочисленный p должен удовлетворить 0 ≤ p ≤ m n.

При вызове "random" метод четырьмя параметрами, разреженная матрица с m строки, n столбцы и в большей части p создаются ненулевые записи. Четвертый параметр g рассматривается как случайный генератор. Матричные записи создаются вызовами g() который должен возвратиться, элементы коэффициента звонят R.

Целочисленный p должен удовлетворить 0 ≤ p ≤ m n.

`sin` — Синус матрицы

sin(A)

Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет расчет sin(elem) для произвольного элемента elem из звонка компонента, FAIL возвращен.

Если некоторые собственные значения A не существуйте в R или не может быть вычислен, затем FAIL возвращен.

Этот метод только существует если R область категории Cat::Field.

Этот метод перегружает функциональный sin для матриц, т.е. можно использовать его в форме sin(A).

`sqrt` — Квадратный корень из матрицы

sqrt(A, <sqrtfunc>)

Возвращенный матричный B с B ² = A, таким образом, что собственные значения B являются квадратными корнями из собственных значений A или FAIL если квадратный корень из матрицы не существует. Для вычисления квадратных корней из собственных значений функция, удовлетворяющая sqrtfunc (a) ² = a для каждого элемента, a содействующего звонка A может быть дан как дополнительный второй аргумент.

Для получения дополнительной информации мы обращаемся к странице справки функционального linalg::sqrtMatrix.

`testeq` — Тестирование на равенство двух матриц

testeq(A, B)

`tr` — Трассировка квадратной матрицы

tr(A)

Если A не является квадратным, сообщение об ошибке выпущено.

`transpose` — Транспонируйте матрицы

transpose(A)

Методы доступа

`_concat` — Горизонтальная конкатенация матриц

_concat(A, B, …)

Этот метод перегружает системную функцию _concat для матриц, т.е. можно использовать его в форме A . B . ..., или в функциональном обозначении: _concat(A, B, ...).

`_index` Индексирование матриц

_index(A, i, j)

_index(A, r1 .. r2, c1 .. c2)

_index(v, i)

_index(v, i1 .. i2)

Если i и j не целые числа, вызов этого метода возвращается в его символьной форме (типа "_index") с оцененными аргументами.

В противном случае сообщение об ошибке дано, если i и j не допустимые индексы строки и столбца, соответственно.

Примечание

Обратите внимание на то, что этот метод использует системную функцию context оценивать запись в контексте среды вызова.

_index(A,r1..r2,c1..c2) возвращает субматрицу A созданный строками A с индексами от r1 к r2 и столбцы A с индексами от c1 к c2.

Этот метод возвращает i th запись векторного v.

Сообщение об ошибке выпущено если v не вектор.

Если i не целое число, вызов _index(v,i) возвращается в его символьной форме (типа "_index") с оцененными аргументами.

В противном случае сообщение об ошибке дано, если i меньше один или больше, чем размерность v.

Примечание

_index(v,i1..i2) возвращает подвектор v, сформированный записями с индексом i1 к i2. См. также метод "op".

Сообщение об ошибке выпущено если v не вектор.

_index перегружает системную функцию _index для матриц, т.е. можно использовать его в форме A[i, j], A[r1..r2, c1..c2]vi и v[i1..i2], соответственно, или в функциональном обозначении: _index(A, ...).

`addCol` — Сложение кратного одному столбцу к кратному другой столбец

addCol(A, i, j, f, <g>)

i и j должны быть положительные целые числа, меньшие, чем или равный количеству столбцов матричного A.

Если f и g не элементы содействующей области R из матричного A и не может быть преобразован в R, FAIL возвращен.

`addRow` — Сложение кратного одной строке к кратному другая строка

addRow(A, i, j, f, g)

i и j должны быть положительные целые числа, меньшие, чем или равный количеству строк матричного A.

`concatMatrix` — Горизонтальная конкатенация матриц

concatMatrix(A, B, …)

`col` — Извлечение столбца матрицы

col(A, c)

Сообщение об ошибке выпущено если c меньше один или больше, чем количество столбцов A.

`delCol` — Удаление столбца матрицы

delCol(A, c)

NIL возвращен если A состоит только из одного столбца.

Сообщение об ошибке выпущено если c меньше один или больше, чем количество столбцов A.

`delRow` — Удаление строки матрицы

delRow(A, r)

NIL возвращен если A состоит только из одной строки.

Сообщение об ошибке выпущено если r меньше один или больше, чем количество строк A.

`evalp` — Оценка матриц полиномов в определенный момент

evalp(A, x = a, …)

Этот метод только задан если R полиномиальный звонок категории Cat::Polynomial.

Этот метод перегружает системную функцию evalp для матриц, т.е. можно использовать его в форме evalp(A, x = a).

`length` — Длина матрицы

length(A)

Этот метод перегружает системную функцию length для матриц, т.е. можно использовать его в форме length(A).

`map` — Примените функцию к матричным компонентам

map(A, f, <p1, p2, …>)

Примечание

Обратите внимание на то, что значения, возвращенные f преобразованы в элементы доменного R только если testargs() возвращает TRUE (т.е. если вы вызываете этот метод от интерактивного уровня MuPAD).

Если testargs() возвращает FALSE, нужно гарантировать тот f возвращает элементы доменного типа R. В противном случае получившаяся матрица будет иметь компоненты, которые не являются элементами кольцевого R компонента!

Примечание

Если функциональный f не сопоставляет нулевой элемент звонка компонента к нулевому элементу, разреженная матрица изменится в плотную матрицу. Это может привести к проблемам памяти при контакте с очень большими (разреженными) матрицами.

Обратите внимание на то, что существует метод "mapNonZeroes" который сопоставляет функцию с ненулевыми записями матрицы только.

Этот метод перегружает системную функцию map для матриц, т.е. можно использовать его в форме map(A, f p1 , p2 , , …).

`mapNonZeroes` — Примените функцию к ненулевым компонентам (разреженной) матрицы

mapNonZeroes(A, f, <p1, p2, …>)

`multCol` — Умножение одного столбца скалярным фактором

multCol(A, i, f)

i должно быть положительное целое число, меньшее, чем или равный количеству столбцов матричного A.

Если f не элемент содействующей области R из матричного A и не может быть преобразован в R, FAIL возвращен.

`multRow` — Умножение одной строки скалярным фактором

multRow(A, i, f)

i должно быть положительное целое число, меньшее, чем или равный количеству строк матричного A.

Если f не элемент содействующей области R из матричного A и не может быть преобразован в R, FAIL возвращен.

`nops` — Количество компонентов матрицы

nops(A)

Этот метод перегружает системную функцию nops для матриц, т.е. можно использовать его в форме nops(A).

`op` — Компонент матрицы

op(A, i)

op(A)

Этот метод возвращает последовательность выражения всех компонентов A.

См. также метод "_index".

Этот метод перегружает системную функцию op для матриц, т.е. можно использовать его в форме op(A, i) и op(A), соответственно.

`row` — Извлечение строки из матрицы

row(A, r)

Сообщение об ошибке выпущено если r меньше один или больше, чем количество строк A.

`setCol` — Заменяя столбец матрицы

setCol(A, c, v)

Сообщение об ошибке выпущено если c меньше один или больше, чем количество строк A.

`setRow` — Заменяя строку матрицы

setRow(A, r, v)

Сообщение об ошибке выпущено если r меньше один или больше, чем количество строк A.

`stackMatrix` — Вертикальная конкатенация матриц

stackMatrix(A, B, …)

Сообщение об ошибке выпущено, если данные матрицы не имеют одинакового числа столбцов.

`subs` — Замена матричных компонентов

subs(A, …)

Примечание

Обратите внимание на то, что значения функции преобразованы в элементы доменного R только если testargs() возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).

Если testargs() возвращает FALSE, нужно гарантировать тот f возвращает элементы доменного типа R. В противном случае, получившаяся матрица, которая имеет доменный тип Dom::Matrix(R), имел бы компоненты, которые не являются элементами доменного R!

Этот метод перегружает системную функцию subs для матриц, т.е. можно использовать его в форме subs(A, ...).

`subsex` — Расширенная замена матричных компонентов

subsex(A, …)

Примечание

Обратите внимание на то, что результаты замен преобразованы в элементы доменного R только если testargs() возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).

Если testargs() возвращает FALSE, нужно гарантировать, что результаты замен имеют доменный тип R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::Matrix(R), имел бы компоненты, которые не являются элементами доменного R!

Этот метод перегружает системную функцию subsex для матриц, т.е. можно использовать его в форме subsex(A, ...).

`subsop` — Замена операнда матричных компонентов

subsop(A, i = x, …)

Примечание

Обратите внимание на то, что x преобразован в доменный R только если testargs() возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).

Если testargs() возвращает FALSEX должен быть элемент R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::Matrix(R), имел бы компоненты, которые не являются элементами доменного R!

См. также метод "set_index".

Этот метод перегружает системную функцию subsop для матриц, т.е. можно использовать его в форме subsop(A, ...).

`swapCol` — Свопинг столбцов матрицы

swapCol(A, c1, c2)

swapCol(A, c1, c2, r1 .. r2)

Сообщение об ошибке выпущено, если один из индексов столбца меньше один или больше, чем количество столбцов A.

swapCol(A,c1,c2,r1..r2) подкачивает столбец с индексом c1 и столбец с индексом c2 из A, но путем взятия только тех компонентов столбца, которые лежат в строках с индексами r1 к r2.

Сообщение об ошибке выпущено, если один из индексов столбца меньше один или больше, чем количество столбцов A, или если один из индексов строки меньше один или больше, чем количество строк A.

`swapRow` — Свопинг строк матрицы

swapRow(A, r1, r2)

swapRow(A, r1, r2, c1 .. c2)

Сообщение об ошибке выпущено, если один из индексов строки меньше один или больше, чем количество строк A.

swapCol(A,r1,r2,c1..c2) подкачивает строку с индексом r1 и строка с индексом r2 из A, но путем взятия только тех компонентов строки, которые лежат в столбцах с индексами c1 к c2.

Сообщение об ошибке выпущено, если один из индексов строки меньше один или больше, чем количество строк A, или если один из индексов столбца меньше один или больше, чем количество столбцов A.

`set_index` — Установка матричных компонентов

set_index(A, i, j, x)

set_index(v, i, x)

Примечание

Обратите внимание на то, что x преобразован в элемент доменного R только если testargs возвращает TRUE и i и j целые числа (например, если вы вызываете этот метод от интерактивного уровня MuPAD). Если x матрица того же типа как A или может быть преобразован в матрицу того же типа как A и индексы i или j области значений, соответствующие субматрице A, затем x заменяет соответствующую субматрицу в A.

В противном случае нужно заботиться тот x имеет доменный тип R.

См. также метод "subsop".

set_index(v,i,x) заменяет i th запись векторного v x.

set_index на векторах перегружает функциональный set_index для матриц, т.е. можно использовать его в форме A[i, j] := x и v[i] := x, соответственно, или в функциональном обозначении: A := set_index(A, i, j, x) или v := set_index(v, i, x).

`zip` — Объедините матрицы покомпонентно

zip(A, B, f, <p1, p2, …>)

Номер строки возвращенной матрицы является минимумом номеров строк A и B. Его номер столбца является минимумом номеров столбцов A и B.

Примечание

Этот метод перегружает системную функцию zip для матриц, т.е. можно использовать его в форме zip(A, B, f p1 , p2 , , …).

Методы преобразования

`convert` — Преобразование в матрицу

convert(x)

FAIL возвращен, если преобразование перестало работать.

x май или быть массивом, матрицей, или списком (подсписков, видят параметр ListOfRows в “Создании Элементов” выше). Их записи должны затем быть конвертируемы в элементы доменного R.

`convert_to` — Матричное преобразование

convert_to(A, T)

T май любой быть DOM_ARRAY, DOM_LIST, или область создается Dom::Matrix или Dom::SquareMatrix. Элементы A должно быть конвертируемо в элементы доменного R.

Используйте функциональный expr преобразовывать A в объект области ядра (см. ниже).

`create` — Определение матриц без преобразований компонента

create(x, …)

Этот метод работает более эффективно, чем если бы вы создаете матрицы путем вызова метода "new" из области, потому что это избегает любого преобразования компонентов. Нужно гарантировать, что компоненты имеют правильный доменный тип, в противном случае ошибки времени выполнения могут быть вызваны.

`expr` — Преобразование матрицы к объекту области ядра

expr(A)

Результатом является массив, представляющий матричный A где каждая запись является объектом области ядра.

Этот метод перегружает системную функцию expr для матриц, т.е. можно использовать его в форме expr(A).

`expr2text` — Преобразование mtrix к строке

expr2text(A)

Этот метод перегружает системную функцию expr2text для матриц, т.е. можно использовать его в форме expr2text(A).

Технические методы

`assignElements` — Несколько присвоение на матрицы

assignElements(A, …)

Присвоенные компоненты должны иметь доменный тип R, неявное преобразование компонентов в элементы доменного типа R не выполняется.

Этот метод перегружает системную функцию assignElements для матриц, т.е. можно использовать его в форме assignElements(A, ...).

`mkSparse` — Преобразование массива или список списков к разреженной структуре

mkSparse(Array)

mkSparse(List)

mkSparse(r, c, List)

'Разреженная структура' s список c одномерные полиномы, который используется, чтобы сохранить нетривиальные элементы столбцов матриц.

mkSparse(List) попытки преобразовать список List в разреженная структура. Результатом является любой FAIL если это не возможно, или список [s, [r, c]], где положительные целые числа r и c размерность соответствующей матрицы. 'Разреженная структура' s список одномерных полиномов, который используется, чтобы сохранить нетривиальные элементы столбцов матриц.

Смотрите параметры List и ListOfRows в “Создании Элементов” выше для допустимых форматов List.

Матрица рассматривается как столбец или вектор-строка, если r или c равно одному. T

mkSparse(r,c,List) попытки преобразовать список List в разреженную структуру, представляющую матрицу размерности r времена c.

Результатом является любой FAIL если это не возможно, или список [s, [r, c]]. 'Разреженная структура' s список одномерных полиномов, который используется, чтобы сохранить нетривиальные элементы столбцов матриц.

Матрица рассматривается как столбец или вектор-строка, если r или c равно одному. T

`print` — Печать матриц

print(A)

Примечание

Обратите внимание на то, что не будет полезно распечатать очень большие разреженные матрицы с большим количеством нулевых коэффициентов таким образом – печать таких матриц может быть сделана при помощи функционального "doprint".

Используйте матричный паз "setPrintMaxSize" установить максимальный размер матриц, которые будут распечатаны как “плотные” массивы с нулевыми записями, отображенными как целое число 0.

`doprint` — Печать больших разреженных матриц

doprint(A)

`setPrintMaxSize` — Установите максимальный размер матриц, которые будут распечатаны как “плотные” массивы

setPrintMaxSize(printMaxSize)

Значение параметра printMaxSize май также быть infinity. В этом случае матрицы произвольного размера распечатаны как “плотные” массивы.

Этот метод возвращает предыдущее значение printMaxSize.

Значением по умолчанию является printMaxSize = 500.

`unapply` — Создайте процедуру из матрицы

unapply(A, <x, …>)

Этот метод перегружает системную функцию fp::unapply для матриц, т.е. можно использовать его в форме fp::unapply(A).

Смотрите также

Области MuPAD

Dom::DenseMatrix | Dom::DenseMatrix | Dom::MatrixGroup | Dom::SquareMatrix

Функции MuPAD

densematrix | matrix

Документация

Dom::Matrix

Синтаксис

Доменное создание

Создание элемента

Описание

Доменное создание

Примечание

Примечание

Создание элемента

Суперобласть

Аксиомы

Категории

Примеры

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Пример 6

Пример 7

Пример 8

Пример 9

Пример 10

Пример 11

Параметры

Опции

Записи

Методы

Математические методы

_divide — Разделите матрицы

_invert — Вычислите инверсию матрицы

_mod — Сопоставьте оператор по модулю с элементами матрицы

_mult — Матрицы мультиплие матрицами, векторами и скалярами

_negate — Инвертируйте матрицу

_plus — Добавьте матрицы

_power — Целочисленная степень матрицы

conjugate — Сопряженное комплексное число матрицы

cos — Косинус матрицы

diff — Дифференцирование матричных компонентов

equal — Тест равенства матриц

exp — Экспоненциал матрицы

expand — Расширьте матричные компоненты

factor — Факторизация диагональной матрицы

float — Приближение с плавающей точкой матричных компонентов

Примечание

fourier — Преобразование Фурье матричных компонентов

gaussElim — Исключение Гаусса для матриц

identity Единичная матрица

int — Интегрирование матричных компонентов

ifourier — Обратное преобразование Фурье матричных компонентов

ilaplace — Обратное Преобразование Лапласа матричных компонентов

iszero — Протестируйте на нулевые матрицы

laplace — Преобразование Лапласа матричных компонентов

matdim — Матричная размерность

norm — Норма матриц и векторов

normal — Упрощение матричных компонентов

nonZeros — Количество ненулевых компонентов матрицы

nonZeroes — Количество ненулевых компонентов матрицы

nonZeroOperands — Возвратите последовательность всех ненулевых операндов

random — Случайная генерация матрицы

sin — Синус матрицы

sqrt — Квадратный корень из матрицы

testeq — Тестирование на равенство двух матриц

tr — Трассировка квадратной матрицы

transpose — Транспонируйте матрицы

Методы доступа

_concat — Горизонтальная конкатенация матриц

_index Индексирование матриц

Примечание

Примечание

addCol — Сложение кратного одному столбцу к кратному другой столбец

addRow — Сложение кратного одной строке к кратному другая строка

concatMatrix — Горизонтальная конкатенация матриц

col — Извлечение столбца матрицы

delCol — Удаление столбца матрицы

delRow — Удаление строки матрицы

evalp — Оценка матриц полиномов в определенный момент

length — Длина матрицы

map — Примените функцию к матричным компонентам

`Dom`::`Matrix`

`_divide` — Разделите матрицы

`_invert` — Вычислите инверсию матрицы

`_mod` — Сопоставьте оператор по модулю с элементами матрицы

`_mult` — Матрицы мультиплие матрицами, векторами и скалярами

`_negate` — Инвертируйте матрицу

`_plus` — Добавьте матрицы

`_power` — Целочисленная степень матрицы

`conjugate` — Сопряженное комплексное число матрицы

`cos` — Косинус матрицы

`diff` — Дифференцирование матричных компонентов

`equal` — Тест равенства матриц

`exp` — Экспоненциал матрицы

`expand` — Расширьте матричные компоненты

`factor` — Факторизация диагональной матрицы

`float` — Приближение с плавающей точкой матричных компонентов

`fourier` — Преобразование Фурье матричных компонентов

`gaussElim` — Исключение Гаусса для матриц

`identity` Единичная матрица

`int` — Интегрирование матричных компонентов

`ifourier` — Обратное преобразование Фурье матричных компонентов

`ilaplace` — Обратное Преобразование Лапласа матричных компонентов

`iszero` — Протестируйте на нулевые матрицы

`laplace` — Преобразование Лапласа матричных компонентов

`matdim` — Матричная размерность

`norm` — Норма матриц и векторов

`normal` — Упрощение матричных компонентов

`nonZeros` — Количество ненулевых компонентов матрицы

`nonZeroes` — Количество ненулевых компонентов матрицы

`nonZeroOperands` — Возвратите последовательность всех ненулевых операндов

`random` — Случайная генерация матрицы

`sin` — Синус матрицы

`sqrt` — Квадратный корень из матрицы

`testeq` — Тестирование на равенство двух матриц

`tr` — Трассировка квадратной матрицы

`transpose` — Транспонируйте матрицы

`_concat` — Горизонтальная конкатенация матриц

`_index` Индексирование матриц

`addCol` — Сложение кратного одному столбцу к кратному другой столбец

`addRow` — Сложение кратного одной строке к кратному другая строка

`concatMatrix` — Горизонтальная конкатенация матриц

`col` — Извлечение столбца матрицы

`delCol` — Удаление столбца матрицы

`delRow` — Удаление строки матрицы

`evalp` — Оценка матриц полиномов в определенный момент

`length` — Длина матрицы

`map` — Примените функцию к матричным компонентам

`mapNonZeroes` — Примените функцию к ненулевым компонентам (разреженной) матрицы

`multCol` — Умножение одного столбца скалярным фактором

`multRow` — Умножение одной строки скалярным фактором

`nops` — Количество компонентов матрицы

`op` — Компонент матрицы

`row` — Извлечение строки из матрицы

`setCol` — Заменяя столбец матрицы

`setRow` — Заменяя строку матрицы

`stackMatrix` — Вертикальная конкатенация матриц

`subs` — Замена матричных компонентов

`subsex` — Расширенная замена матричных компонентов

`subsop` — Замена операнда матричных компонентов

`swapCol` — Свопинг столбцов матрицы

`swapRow` — Свопинг строк матрицы

`set_index` — Установка матричных компонентов

`zip` — Объедините матрицы покомпонентно

`convert` — Преобразование в матрицу

`convert_to` — Матричное преобразование

`create` — Определение матриц без преобразований компонента

`expr` — Преобразование матрицы к объекту области ядра

`expr2text` — Преобразование mtrix к строке

`assignElements` — Несколько присвоение на матрицы

`mkSparse` — Преобразование массива или список списков к разреженной структуре

`print` — Печать матриц

`doprint` — Печать больших разреженных матриц

`setPrintMaxSize` — Установите максимальный размер матриц, которые будут распечатаны как “плотные” массивы

`unapply` — Создайте процедуру из матрицы