`int`::`addpattern`

Добавьте шаблоны для интегрирования

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

int::addpattern(pat, x, res, <[var, …], <[cond, …]>>)
int::addpattern(pat, x = u .. v, res, <[var, …], <[cond, …]>>)

Описание

int::addpattern(pat, x, res) преподает int использовать.

int::addpattern(pat, x=u..v, res) преподает int это.

Значительная часть компьютерной алгебры способности к интегрированию системы происходит от математического сопоставления с образцом. Сопоставитель MuPAD^® может быть расширен во времени выполнения с int::addpattern.

Если далее ограниченный условиями в пятом аргументе, переменные шаблона, перечисленные в четвертом аргументе, не представляют произвольные выражения MuPAD, не содержащие переменную интегрирования, x.

Любой идентификатор может использоваться в качестве переменной интегрирования в вызове int::addpattern, и любой идентификатор может использоваться в вызовах int. Они не должны быть идентичными.

Для определенного интегрирования каждое связанное интегрирование является или арифметическим выражением, которое может содержать переменные шаблона или идентификатор, который может использоваться в качестве переменной в терминах условия и результате.

Пользователи могут включать дополнительные условия путем предоставления дополнительных аргументов. Эти условия, а также результат, защищены от преждевременной оценки, т.е. не необходимо записать hold( _not @ iszero )(a^2-b), простой not iszero(a^2-b) достаточен.

Различие между not iszero(a^2-b) и a^2-b <> 0 когда дали, когда условие состоит в том, что последний учитывает asuumptions на идентификаторах, с которыми сталкиваются, в то время как первое не делает. См. Пример 4.

Шаблоны введены int::addpattern также используются в рекурсивных вызовах интегратора и автоматически расширены, чтобы включать простые приложения интегрирования заменой переменных. См. Пример 1.

Шаблоны добавляются int::addpattern не заменяются более поздними вызовами, они остаются активными. int выбирает самый простой найденный результат. Нет никакого способа удалить шаблоны, однажды добавленные. См. Пример 5.

Взаимодействия среды

Вызов int::addpattern изменяет выражения, возвращенные будущими вызовами int. Кроме того, помнившие значения предыдущих вызовов int забыты.

Примеры

Пример 1

Не удивительно, MuPAD не знает, как интегрировать функциональный foo:

int(foo(x), x)

Мы добавляем шаблон для этой функции:

int::addpattern(foo(x), x, foo(x)^x)

int(foo(x), x)

Обратите внимание на то, что этот шаблон также используется косвенно:

int(x*foo(x^2), x)

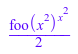
intlib::byparts(int(foo(x)*sin(x), x), foo(x))

Пример 2

Определенные интегралы могут быть добавлены так же. Обратите внимание на то, что результат не зависит от переменной интегрирования:

int::addpattern(wilma(x), x=0..1, fred)

int(wilma(x), x=0..1)

Вышеупомянутый шаблон не будет совпадать с интегралами различным границам интегрирования:

int(wilma(x), x=0..2)

Границы интегрирования могут также содержать переменные, происходящие в шаблоне или результате:

int::addpattern(wilma(x, a), x=0..a, fred(a), [a])

int(wilma(x,2), x=0..2)

Пример 3

Переменная интегрирования в вызове int::addpattern не должен быть эквивалентным используемый в вызове интегрирования:

int::addpattern(1/(t^2*(ln(t)+1)), t, -E*Ei(ln(t)+1))

int(cos(y)/sin(y)^2/(ln(sin(y)) + 1), y)

Пример 4

Условия проверяются с помощью is и поэтому реагируйте на предположения:

int::addpattern(1/(a+b*tan(x)^2), x,
                x/(a-b) 
                - b/(2*(a-b)*sqrt(-a*b))
                 * ln((b*tan(x)-sqrt(-a*b))
                     /(b*tan(x)+sqrt(-a*b))),
                [a, b],
                [a*b < 0])

int::addpattern(1/(a+b*tan(x)^2), x,
                x/(a-b)
                - b/((a-b)*sqrt(a*b))
                 * arctan(b*tan(x)/
                          sqrt(a*b)),
                [a, b],
                [a*b > 0])

int(1/(3+a*tan(x)^2), x) assuming a > 0

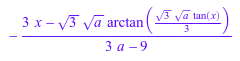
int(1/(3+a*tan(x)^2), x) assuming a < 0

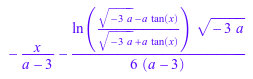
Если или условиям не удовлетворяют или замена значениями в урожаи результата ошибка, шаблон проигнорирован. В шаблонах выше, случай a = b вызывает деление на нуль. Нет никакой потребности включать условие принять меры против этого случая, тем не менее, MuPAD просто вычисляет интеграл, как обычно:

int(1/(3+3*tan(x)^2), x)

Пример 5

Примите, что мы добавили следующий шаблон:

int::addpattern(f(x), x, f(x)^x):

Теперь f является довольно родовым названием, таким образом, мы могли позже рассматривать его как различную функцию и попытаться переопределить ее антипроизводную:

int::addpattern(f(x), x, 1/sin(f(x))):

int(f(x), x)

Что произошло?

Как оказалось, int::addpattern просто добавил новый шаблон, и начиная с f (x) ^x рассматривается “более простым”, чем, результат первого добавленного шаблона все еще возвращен.

Это поведение разумно, поскольку может быть несколько способов представлять антипроизводную и в зависимости от значений параметров, один или другой может быть предпочтительным:

int::addpattern(f(a, x), x, x*f1(a, x^a), [a]):
int::addpattern(f(a, x), x, x*f2(a, x^(1-a)), [a]):

int(f(0, x), x)

int(f(1, x), x)

int(f(a, x), x)

Параметры

`pat`	Шаблон, чтобы соответствовать: арифметическое выражение в `x`.
`x`	Переменная интегрирования: `identifier`.
`u .. v`	Интервал интегрирования для определенного интеграла: арифметические выражения или идентификаторы.
`res`	Антипроизводный шаблон: арифметическое выражение
`[var, …]`	“переменные шаблона”: заполнители в `pat` и `ret`, т.е. `identifiers` это не представляет себя, но почти произвольные выражения MuPAD, не содержащие `x` и ограниченный условиями в пятом параметре.
`[cond, …]`	Условия на переменных шаблона

Возвращаемые значения

Объект типа DOM_NULL

Смотрите также

Функции MuPAD

int

Документация