`int`

Определенные и неопределенные интегралы

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Для неопределенного интегрирования в MATLAB^® смотрите int Symbolic Math Toolbox™ функция. Для численного интегрирования смотрите integral функция.

Синтаксис

int(f, x)
int(f, x = a .. b, options)

Описание

int(f, x) вычисляет неопределенный интеграл.

int(f, x = a..b) вычисляет определенный интеграл.

int(f, x) определяет функциональный F, таким образом что. Функциональный F (x) называется антипроизводной f (x). Результаты возвращены int не включайте константы интегрирования.

Для неопределенных интегралов, int неявно принимает что переменная интегрирования x isreal. Для определенных интегралов, int ограничивает переменную интегрирования x к заданному интервалу интегрирования [a, b] из типа Type::Interval. Если одна или обе границы интегрирования a и b не являются числовыми, int принимает тот a <= b если вы явным образом не задаете в противном случае. По умолчанию, int не делает предупреждений о проблемах об этих предположениях. Чтобы вывести предупреждения об использовании неявных предположений, установите значение intlib::printWarnings к TRUE.

В общем случае результат int не требуется, чтобы быть допустимым для всех комплексных чисел x. Например, идентичность только допустима для действительных значений x. Поэтому также допустимо только для действительных значений x.

Можно задать собственные предположения о переменной интегрирования. Если эти предположения не конфликтуют с предположением по умолчанию, что переменная действительна или с интервалом интегрирования, то MuPAD^® использует ваши предположения. В противном случае, int функция выдает предупреждение и изменяет предположения. Используйте intlib::printWarnings включить или отключить предупреждения.

Если вы вычисляете неопределенный интеграл и задаете свойства переменной интегрирования, которые описывают подмножество вещественных чисел, MuPAD принимает, что переменная действительна. В противном случае система использует временное предположение, что переменная интегрирования является комплексной. Это предположение содержит только во время этого конкретного интегрирования.

Если вы вычисляете определенный интеграл и задаете свойства, которые конфликтуют с интервалом интегрирования, int использует интервал интегрирования.

int может возвратить результаты с разрывами, даже если подынтегральное выражение непрерывно.

Методы интегрирования, такие как поиск по таблице или интегрирование Риша для неопределенного интеграла, могут добавить новые разрывы во время процесса интеграции. Эти новые разрывы появляются, потому что антипроизводные могут потребовать введения комплексных логарифмов. Комплексные логарифмы имеют разрыв скачка, когда аргумент пересекает отрицательную вещественную ось, и алгоритмы интегрирования иногда не могут находить представление, где эти скачки отменяют.

Если вы вычисляете определенный интеграл первым вычислением неопределенного интеграла и затем заменой контурами интегрирования в результат, помните, что неопределенное интегрирование может произвести разрывы. Если это делает, необходимо исследовать разрывы в интервале интегрирования.

Если MuPAD не может найти решение закрытой формы для интеграла и не может доказать, что такая форма не существует, это возвращает неразрешенный интеграл. В этом случае можно аппроксимировать интеграл численно или попытаться вычислить последовательное расширение интеграла. Смотрите Пример 2 и Пример 3.

Можно аппроксимировать определенный интеграл численно с помощью numeric::int или float. Числовое приближение определенного интеграла только работает когда float функция может преобразовать контуры a и b из интервала интегрирования к числам с плавающей запятой. Смотрите Пример 2.

int не может найти закрытую форму определенного интеграла из-за сингулярности подынтегрального выражения в интервале интегрирования. Если интеграл не существует в строгом математическом смысле, int возвращает значение undefined. В этом случае попытайтесь использовать предположения. В качестве альтернативы используйте PrincipalValue опция, чтобы вычислить более слабую форму определенного интеграла вызвала Главное значение Коши. Эта форма интеграла может существовать даже при том, что стандартное интегральное значение не определено. Смотрите Пример 6.

В общем случае производная результата совпадает с f на плотном подмножестве вещественных чисел (или, если вы используете предположения на переменной интегрирования, подмножестве вещественных чисел, заданных этими предположениями).

Не всегда возможно решить алгоритмически, если и f эквивалентны. Причиной является так называемая нулевая эквивалентная проблема, которая в целом неразрешима.

Взаимодействия среды

int чувствительно к свойствам идентификаторов, установленных assume. Смотрите пример 6.

Примеры

Пример 1

Вычислите неопределенные интегралы и:

int(1/x/ln(x), x)

int(1/(x^2 - 8), x)

Вычислите определенный интеграл на интервале [e, e ²]:

int(1/x/ln(x), x = exp(1)..exp(2))

При вычислении определенных интегралов можно использовать бесконечности в качестве контуров интервала интегрирования:

int(exp(-x^2), x = 0..infinity)

Можно вычислить кратные интегралы. Например, вычислите следующий определенный кратный интеграл:

int(int(int(1, z = 0..c*(1 - x/a - y/b)),
        y = 0..b*(1 - x/a)), x = 0..a)

Пример 2

Используйте int вычислить этот определенный интеграл. Начиная с int не может найти закрытую форму этого интеграла, это возвращает неразрешенный интеграл:

S := int(sin(cos(x)), x = 0..1)

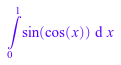
Используйте float функционируйте, чтобы аппроксимировать интеграл численно:

float(S)

В качестве альтернативы используйте numeric::int функция, которая быстрее, потому что она не включает символьной предварительной обработки:

numeric::int(sin(cos(x)), x = 0..1)

Пример 3

Используйте int вычислить этот неопределенный интеграл. Начиная с int не может найти закрытую форму этого интеграла, это возвращает неразрешенный интеграл:

int((x^2 + 1)/sqrt(sqrt(x + 1) + 1), x)

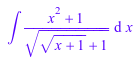
Используйте series функция, чтобы вычислить последовательное расширение интеграла:

series(%, x = 0)

В качестве альтернативы вычислите последовательное расширение подынтегрального выражения, и затем интегрируйте результат. Этот подход быстрее, потому что он не пытается интегрировать исходное выражение. Это интегрирует приближение (последовательное расширение) исходного выражения:

int(series((x^2 + 1)/sqrt(sqrt(x + 1) + 1), x = 0), x)

Пример 4

IgnoreAnalyticConstraints опция применяет набор чисто алгебраических упрощений включая равенство суммы логарифмов и логарифма продукта. Используя эту опцию, вы получаете более простой результат, но тот, который может быть неправильным для некоторых значений переменных:

int(ln(x) + ln(y) - ln(x*y), x, IgnoreAnalyticConstraints)

Не используя эту опцию, вы получаете следующий результат, который допустим для всех значений параметров:

int(ln(x) + ln(y) - ln(x*y), x)

Результаты получены с IgnoreAnalyticConstraints может быть не обычно допустимым:

f := int(ln(x) + ln(y) - ln(x*y), x):
g := int(ln(x) + ln(y) - ln(x*y), x, IgnoreAnalyticConstraints):
simplify([f, g]) assuming x = -1 and y = -1

Пример 5

По умолчанию, int возвращает этот интеграл как кусочный объект, где каждая ветвь соответствует особому значению (или область значений значений) символьного параметра t:

int(x^t, x)

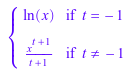
Чтобы игнорировать особые регистры значений параметров, используйте IgnoreSpecialCases:

int(x^t, x, IgnoreSpecialCases)

Пример 6

Вычислите этот определенный интеграл, где подынтегральное выражение имеет полюс во внутренней части интервала интегрирования. Математически, этот интеграл не задан:

int(1/(x - 1), x = 0..2)

Однако Главное значение Коши интеграла существует. Используйте PrincipalValue опция, чтобы вычислить Главное значение Коши интеграла:

hold(int)(1/(x - 1), x = 0..2, PrincipalValue) =
     int( 1/(x - 1), x = 0..2, PrincipalValue)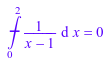

Для подынтегральных выражений параметрами, int может не мочь решить, имеет ли подынтегральное выражение полюса в интервале интегрирования. В этом случае, int возвращает кусочно заданную функцию или неразрешенный интеграл:

int(1/(x - a), x = 0..2)

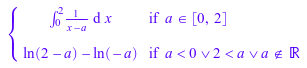
int не вызывает функции упрощения для его результатов. Упростить результаты, возвращенные int, используйте evalупрощение, или Simplify:

Simplify(eval(%))

Получившееся кусочное выражение имеет только одну ветвь. Если параметр a не удовлетворяет этому условию, интегралом является undefined.

Параметры

`f`	Подынтегральное выражение: арифметическое выражение, представляющее функцию в `x`
`x`	Переменная интегрирования: идентификатор
`aB`	Контуры: арифметические выражения

Опции

IgnoreAnalyticConstraints

Когда вы используете эту опцию, int применяет эти правила упрощений к подынтегральному выражению:

ln (a) + ln (b) = ln (a b) для всех значений a и b. В частности:
для всех значений a, b и c
ln (a ^b) = b ln (a) для всех значений a и b. В частности:
для всех значений a, b и c
Если f и g являются стандартными математическими функциями и f (g (x)) = x для всех маленьких положительных чисел, f (g (x)) =, x принят, чтобы быть допустимым для всего комплексного x. В частности:
- arcsin (sin (x)) = x, arccos (cos (x)) = x, arctan (tan (x)) = x
- arcsinh (sinh (x)) = x, arccosh (cosh (x)) = x, arctanh (tanh (x)) = x
- для всех значений k

Используя эту опцию, можно получить простые решения для некоторых интегралов, для которых прямой вызов интегратора возвращает сложные результаты. При использовании этой опции интегратор не проверяет правильность и полноту результата. Смотрите Пример 4.

IgnoreSpecialCases

Если интегрирование требует анализа случая, игнорируйте регистры, которые требуют, чтобы один или несколько параметров были элементами сравнительно маленького набора, такими как фиксированное конечное множество или набор целых чисел.

При использовании этой опции, int попытки сократить количество ветвей в кусочных объектах. MuPAD находит уравнения и членства в сравнительно маленьких наборах. Во-первых, MuPAD пытается доказать такие уравнения и членства при помощи механизма свойства. Если механизм свойства доказывает уравнение, или членство верно, MuPAD сохраняет тот оператор. В противном случае MuPAD может заменить тот оператор на FALSE значения.

Например, если механизм свойства не может доказать, что знаменатель равен нулю, MuPAD рассматривает этот знаменатель как ненулевой. Эта опция может значительно сократить количество кусочных объектов в результате.

Смотрите пример 5.

PrincipalValue

Вычислите Главное значение Коши интеграла.

Если внутренняя часть интервала интегрирования содержит полюса подынтегрального выражения, или контурами является a = - ∞ и b = ∞, то определенный интеграл не может существовать в строгом математическом смысле. Однако, если подынтегральное выражение изменяет знак во всех полюсах в интервале интегрирования, можно вычислить более слабую форму определенного интеграла, названного Главным значением Коши. В этой форме так называемые бесконечные части интеграла налево и справа от полюса отменяют друг друга. Когда вы используете PrincipalValue опция, int вычисляет Главное значение Коши. Если определенный интеграл существует в строгом математическом смысле, он совпадает с Главным значением Коши. Смотрите Пример 6.

Возвращаемые значения

арифметическое выражение

Перегруженный

f

Ссылки

[1] Бронштайн, M. “Объединение расширения Liouvillian”. AAECC применимая алгебра в разработке, коммуникации и вычислении. 1: 5–24, 1990.

[2] Бронштайн, M. “Трансцендентальное дифференциальное уравнение Риша”. Журнал символьного расчета. 9: 49–60, 1990.

[3] Бронштайн, M. “Символьное интегрирование I: трансцендентные функции”. Спрингер. 1997.

[4] Эпштейн, H. I. и Б. Ф. Кэвинесс. “Теорема Структуры для Элементарных функций и ее Приложения к Единичной проблеме”. Международный журнал Информатики и вычислительной техники. 8: 9–37, 1979.

[5] Fakler, W. “Vereinfachen von komplexen Integralen reeller Funktionen” . № 1 mathPAD 9: 5-9, 1999.

[6] Геддес, K. O. С. Р. Кзэпор и Г. Лэбэн. “Алгоритмы для компьютерной алгебры”. 1992.

Документация