intlib::changevarЗамена переменной
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
intlib::changevar(integral, eq, <var>)
intlib::changevar(integral, eq) выполняет замену переменной для неопределенных и определенных интегралов.
Математически, правило замены официально задано для неопределенных интегралов как
и для определенных интегралов как
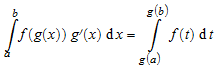
intlib::changevar(integral, eq) выполняет в integral замена переменной задана eq и возвращает неоцененный новый интеграл. Можно использовать eval команда, чтобы найти закрытую форму этого нового интеграла, если это закрытая форма существует.
intlib::changevar работает на неопределенный, а также на определенные интегралы.
Первый аргумент должен содержать символьный интеграл типа "int". Такое выражение может быть получено с hold или freeze. Смотрите пример 1.
Если больше чем две переменные происходят в eq, новая переменная должна быть дана как третий аргумент.
Если MuPAD® не может решить данное уравнение eq ошибка произойдет.
Как первый пример мы выполняем замену переменной для интеграла
. При помощи hold функция мы гарантируем, что первый аргумент имеет тип "int":
intlib::changevar(hold(int)(f(x + c), x = a..b),
t = x + c, t)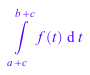
Обратите внимание на то, что в этом случае уравнение замены имеет две дальнейших переменные помимо x. Таким образом необходимо задать новую переменную интегрирования в качестве третьего аргумента.
В следующем примере мы используем метод замены переменной в решении интеграла
. Сначала мы выполняем преобразование t = ln (x):
f1 := intlib::changevar(hold(int)(cos(ln(x)), x),
t = ln(x), t)
Теперь мы можем оценить интеграл с интегратором MuPAD:
f2:=eval(f1)
Наконец мы возвращаем переменную t к x и получаем результат:
F := simplify(f2 | t = ln(x))
Мы можем также проверить решение интеграла:
simplify(diff(F,x) - cos(ln(x)))
|
Интеграл: арифметическое выражение, содержащее символьный |
|
Уравнение, задающее новую переменную интегрирования в терминах старой: уравнение |
|
Новая переменная интегрирования: идентификатор |
Арифметическое выражение.