linalg::charmatХарактеристическая матрица
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::charmat(A, x)
linalg::charmat(A, x) возвращает характеристический матричный x In - A n ×n матричный A, где I n обозначает n ×n единичная матрица.
Звонок компонента A должен быть коммутативный звонок, т.е. область категории Cat::CommutativeRing.
Характеристический матричный M = x In - A A может быть оценен в точке x = u через evalp(M, x = u). Смотрите пример 2.
Мы задаем матрицу по рациональным числам:
A := Dom::Matrix(Dom::Rational)([[1, 2], [3, 4]])
![]()
и вычислите характеристическую матрицу A в переменной x:
MA := linalg::charmat(A, x)
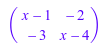
Определитель матричного MA полином в x, характеристический полином матричного A:
pA := det(MA)
![]()
domtype(pA)
![]()
Конечно, мы можем вычислить характеристический полином A непосредственно через linalg::charpoly:
linalg::charpoly(A, x)
![]()
Результат имеет тот же доменный тип как полиномиальный pA.
Мы задаем матрицу по комплексным числам:
B := Dom::Matrix(Dom::Complex)([[1 + I, 1], [1, 1 - I]])
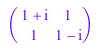
Характеристическая матрица B в переменной z:
MB := linalg::charmat(B, z)
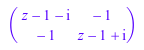
Мы оцениваем MB в z = i и получают матрицу:
evalp(MB, z = I)
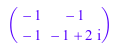
Обратите внимание на то, что это - матрица доменного типа Dom::Matrix(Dom::Complex):
domtype(%)
![]()
|
Квадратная матрица области категории |
|
Матрица доменного Dom::Matrix(Dom::DistributedPolynomial([x], R)) или Dom::DenseMatrix(Dom::DistributedPolynomial([x], R)), где R звонок компонента A.