linalg::condЧисло обусловленности матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::cond(M, <1 | 2 | Spectral | Infinity | Frobenius>)
linalg::cond(M) вычисляет число обусловленности матрицы, заданной
. По умолчанию матричная Бесконечность нормы используется linalg::cond.
linalg::cond(M) краткая форма linalg::cond(M, Infinity).
linalg::cond(M, k) вычисляет число обусловленности матрицы M, заданной
.
Для получения дальнейшей информации смотрите страницу справки norm.
Мы задаем 3×3 матрица А.
A := matrix(3,3, [[1,0,3],[-4,2,0],[0,3,-2]])
Теперь мы вычисляем число обусловленности для некоторых матричных норм.
linalg::cond(A)
linalg::cond(A, Infinity)
linalg::cond(A, 1)
linalg::cond(A, Frobenius)
Результат для спектральной нормы является слишком комплексным, таким образом, мы хотим плавающую оценку. Крошечная мнимая часть является округляющимся артефактом:
linalg::cond(A, 2); float(%)
Если A будет содержать по крайней мере одно число с плавающей запятой, результат будет вычислен численно.
B := A: B[1,1] := float(B[1,1]): linalg::cond(B, 2)
Мы задаем 2×2 матричный C.
C := matrix([[1,-2],[3,-4]])
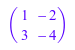
Теперь мы вычисляем число обусловленности C для некоторых матричных норм.
linalg::cond(C,1)
linalg::cond(C,Infinity)
linalg::cond(C,Frobenius); Simplify(%);
Гильбертовы матрицы очень плохо обусловлены:
linalg::cond( linalg::hilbert(3) )
linalg::cond( linalg::hilbert(5) )
linalg::cond( linalg::hilbert(7) )
|
Квадратная матрица доменного типа |
|
Индекс матричной нормы. |
Арифметическое выражение.