normВычислите норму матрицы, вектора или полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
norm(M, <1 | 2 | Frobenius | Infinity | Spectral>) norm(v, <Frobenius | Infinity | kv>) norm(p, <kp>) norm(f, <vars>, <kp>)
norm(M, kM) вычисляет норму индекса kM из матричного M.
norm(v, kv) вычисляет норму индекса kv из векторного v.
norm(p, kp) вычисляет норму индекса kp из полиномиального p.
В MuPAD® нет никакого различия между матрицами и векторами: вектор является матрицей размерности 1×n или n ×1, соответственно.
Для m ×n матричный M = (M ij) с min (m, n)> 1, только 1 норма (максимальная сумма столбца)
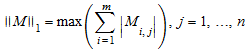 ,
,
норма Фробениуса
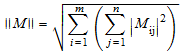 ,
,
спектральная норма
![]() ,
,
где ϕ является самым большим собственным значением A H A и infinity - норма (максимальная сумма строки)
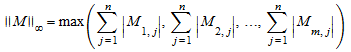
может быть вычислен. 1 норма и Infinity- норма является нормами оператора относительно соответствующих норм по векторным пространствам, на которые реагирует матрица.
Для векторов v = (v i), представленный матрицами размерности 1×n или n ×1, нормы с произвольными положительными целочисленными индексами k, а также Infinity может быть вычислен. Для целых чисел k> 1, векторными нормами дают
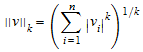
для вектор-столбцов, а также для векторов-строк.
Для индексов 1, Infinity, и Frobenius, векторные нормы даны соответствующими матричными нормами. Для вектор-столбцов 1 норма является нормой суммы
![]() ,
,
Infinity- норма является максимальной нормой
![]()
(это - предел k - нормы, когда k стремится к бесконечности).
Для векторов-строк 1 норма является максимальной нормой, пока Infinity- норма является нормой суммы.
Норма Фробениуса совпадает с norm(v, 2) и для вектор-столбцов и для векторов-строк.
См. пример 2.
Матрицы и векторы могут содержать символьные записи. Никакое внутреннее преобразование плавающее не применяется.
Для матричных и векторных норм также обратитесь к странице справки Dom::Matrix (обратите внимание что функциональный matrix генерирует матрицы типа Dom::Matrix()).
Для полиномов p с коэффициентами c i нормами дают
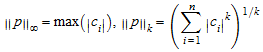 .
.
Также многомерные полиномы приняты norm. Коэффициенты относительно всего indeterminates учтены.
Для полиномов только могут быть вычислены числовые нормы. Коэффициенты полинома не должны содержать символьные параметры, которые не могут быть преобразованы в числа с плавающей запятой. Коэффициенты, содержащие символьные числовые выражения, такие как PI+1, sqrt(2) и т.д. приняты. Внутренне, они преобразованы в числа с плавающей запятой. См. Пример 3.
Для индексов k> 1, norm(p, k) всегда возвращает число с плавающей запятой. 1 норма приводит к точному результату, если все коэффициенты являются целыми числами или рациональными числами. infinity - норма norm(p) приводит к точному результату, если коэффициент самой большой величины является целым числом или рациональным числом. Во всех других случаях, также 1 норма и infinity - норма производят числа с плавающей запятой. См. Пример 3.
Поскольку полиномы по коэффициенту звонят IntMod(m)норма производит ошибку.
Если содействующий звонок полинома является областью, это должно реализовать метод "norm". Этот метод должен возвратить норму коэффициентов как номер или как числовое выражение, которое может быть преобразовано в число с плавающей запятой через float. С содействующими нормами![]() ,
, norm(p) вычисляет максимальную норму![]() ;
; norm(p, k) вычисляет![]() .
.
Многочленное выражение f внутренне преобразован в полиномиальный poly(f). Если список indeterminates задан, норма полиномиального poly(f, vars) вычисляется.
Для полиномов и многочленных выражений, нормы вычисляются функцией системного ядра.
Мы вычисляем различные нормы 2×3 матрица:
M := matrix([[2, 5, 8], [-2, 3, 5]]): norm(M) = norm(M, Infinity), norm(M, 1), norm(M, Frobenius), norm(M, Spectral)
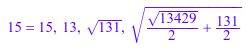
Для матриц, norm приводит к точным символьным результатам:
M := matrix([[2/3, 63, PI],[x, y, z]]): norm(M)
![]()
norm(M, 1)
![]()
norm(M, Frobenius)
![]()
delete M:
Вектор-столбец col и вектор-строка row рассматриваются:
col := matrix([x1, PI]): row := matrix([[x1, PI]]): col, row
![]()
norm(col, 2) = norm(row, 2)
![]()
norm(col, 3) = norm(row, 3)
![]()
Обратите внимание на то, что нормы индекса 1 и Infinity обменивались значениями для вектор-столбцов и векторов-строк:
norm(col, 1) = norm(row, Infinity)
![]()
norm(col, Infinity) = norm(row, 1)
![]()
delete col, row:
Нормы некоторых полиномов вычисляются:
p := poly(3*x^3 + 4*x, [x]): norm(p), norm(p, 1)
![]()
Если коэффициенты не являются целыми числами или рациональными числами, автоматическое преобразование в числа с плавающей запятой происходит:
p := poly(3*x^3 + sqrt(2)*x + PI, [x]): norm(p), norm(p, 1)
![]()
Числа с плавающей точкой всегда производятся для индексов, больше, чем 1:
p := poly(3*x^3 + 4*x + 1, [x]): norm(p, 1), norm(p, 2), norm(p, 5), norm(p, 10), norm(p)
![]()
delete p:
Нормы некоторых многочленных выражений вычисляются:
norm(x^3 + 1, 1), norm(x^3 + 1, 2), norm(x^3 + PI)
![]()
Следующий вызов дает к ошибке, потому что выражение рассматривается как полином в x. Следовательно, символьные коэффициенты 6 y и 9 y2 найдены, которые не приняты:
f := 6*x*y + 9*y^2 + 2: norm(f, [x])
Error: Invalid argument. [norm]
Как двумерный полином с indeterminates x и y, коэффициенты равняются 6, 9, и 2. Теперь нормы могут быть вычислены:
norm(f, [x, y], 1), norm(f, [x, y], 2), norm(f, [x, y])
![]()
delete f:
|
Матрица A доменного типа |
|
Вектор (1-мерная матрица) |
|
Положительное целое число как индекс векторной нормы. |
| |
| |
|
Список идентификаторов или индексированных идентификаторов, интерпретированных как indeterminates |
|
Индекс нормы полинома: вещественное число, больше или равное, чем 1. Если никакой индекс не задан, максимальная норма (бесконечности индекса) вычисляется. |
|
Вычисляет норму Фробениуса для векторов и матриц. |
|
Вычисляет Норму по бесконечности для векторов и матрицы. |
|
Вычисляет Спектральную норму для матриц. |
Арифметическое выражение.
fP