linalg::hessenberg
Матрица Хессенберга
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
linalg::hessenberg(A, <All>)
Описание
linalg::hessenberg(A) возвращает (верхнюю) матрицу Хессенберга H.
linalg::hessenberg Исключение Гаусса использования без поворота. Нет никакой специальной реализации для матриц с компонентами с плавающей точкой.
Звонок компонента A должно быть поле, т.е. область категории Cat::Field.
Примеры
Пример 1
Рассмотрите матрицу:
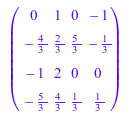
A := Dom::Matrix(Dom::Rational)( [[0, 1, 0, -1], [-4/3, 2/3, 5/3, -1/3], [-1, 2, 0, 0], [-5/3, 4/3, 1/3, 1/3]] )
Следующая матрица Хессенберга похожа на A:
H := linalg::hessenberg(A)
Если соответствующая матрица преобразования необходима также, вызовите linalg::hessenberg с опцией All:
[H, P] := linalg::hessenberg(A, All)
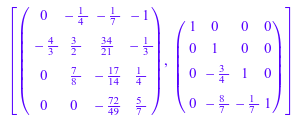
Затем P является несингулярной матрицей, таким образом, что продукт P AP-1 равен H:
P * A * P^(-1)
Параметры
|
Квадратная матрица области категории |
Опции
|
Возвращает список |
Возвращаемые значения
Матрица того же доменного типа как A, или список [H, P] когда опция All дан.
Ссылки
Ссылка: K.-H. Kiyek, Ф. Шварц: алгебра Lineare. Teubner Studienbücher Mathematik, Б.Г. Теубнер Штутгарт, Лейпциг, 1999.
Алгоритмы
n ×n матричный A = (a i, j) 1 ≤ i ≤ n, 1 ≤ j ≤ n называется (верхней) матрицей Хессенберга, если следующее содержит: a i, j = 0 для всего i, j ∈ {1, …, n} с i> j.
Для каждой квадратной матрицы A по полю там существует матрица Хессенберга, похожая на A. В общем случае верхняя матрица Хессенберга не уникальна.