`linalg`::`smithForm`

Нормальная форма Смита матрицы

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

linalg::smithForm(A, <var>, <All>)

Описание

linalg::smithForm(A) вычисляет нормальную форму Смита n - размерная квадратная матрица A, который является n ×n диагональный матричный S, такой, что S _{i - 1, i - 1} делит S _{i, i} для i = 2, …, n.

Нормальная форма Смита матричного A уникально.

Звонок компонента A должно быть Евклидово кольцо, то есть, область категории Cat::EuclideanDomain.

linalg::smithForm(A, var) возвращает нормальную форму Смита A, предположение, что элементы A одномерные полиномы в переменной var. Если A не содержит var, затем smithForm(A) и smithForm(A,var) возвратите различные результаты.

linalg::smithForm(A, <var>, All) возвращает список [S, U, V], где S нормальная форма Смита A, и U и V unimodular матрицы преобразования, такие что S = U*A*V. Можно использовать All опция с или не задавая переменную var.

Примеры

Пример 1

Создайте следующую матрицу целых чисел.

A := matrix([[9, -36, 30], [-36, 192, -180], [30, -180, 180]])

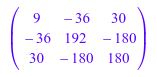
Найдите нормальную форму Смита этой матрицы.

linalg::smithForm(A)

Используйте All опция, чтобы найти соответствующие матрицы преобразования.

[S, U, V] := linalg::smithForm(A, All)

Проверьте тот S = U*A*V.

S = U*A*V

Пример 2

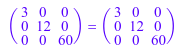
Создайте следующую матрицу полиномов.

B := matrix([[-(x - 3)^2*(x - 2),(x - 3)*(x - 2)*(x - 4)],
             [(x - 3)*(x - 2)*(x - 4),-(x - 3)^2*(x - 4)]
            ])

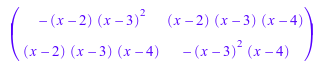
Найдите нормальную форму Смита этой матрицы.

linalg::smithForm(B)

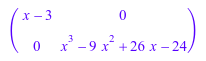
Используйте All опция, чтобы найти соответствующие матрицы преобразования.

[U, S, V] := linalg::smithForm(B, All)

Пример 3

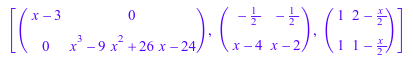
Если матрица не содержит конкретную переменную, и вы вызываете linalg::smithForm указывание, что переменная в качестве второго аргумента, затем результат отличается от того, что вы получаете, не указывая ту переменную. Например, создайте матрицу, которая не содержит переменных.

A := matrix([[9, -36, 30], [-36, 192, -180], [30, -180, 180]])

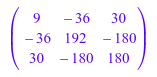
Вызовите linalg::smithForm определение переменной x в качестве второго аргумента. В этом случае, linalg::smithForm принимает что элементы A одномерные полиномы в x.

linalg::hermiteForm(A, x)

Вызовите linalg::smithForm не задавая переменные. В этом случае, linalg::smithForm обработки A как матрица целых чисел.

linalg::hermiteForm(A)

Параметры

`A`	Квадратная матрица области категории `Cat::Matrix`

Опции

All

Возвращает список [S, U, V], где S нормальная форма Смита A, и U и V unimodular матрицы преобразования, такие что S = U*A*V.

Возвращаемые значения

Матрица того же доменного типа как A. С опцией All, linalg::smithForm возвращает список [S, U, V], где S матрица того же доменного типа как A, и U и V соответствующие матрицы преобразования.

Алгоритмы

n ×n матричный S = (s _ij) с коэффициентами в Евклидово кольце является нормальной формой Смита матрицы, если S является диагональной матрицей (с неотрицательными коэффициентами в случае кольцевого ℤ), такой, что s _{i, i} делит s _{i + 1, i + 1} для всего i <n.

Документация