linalg::jordanFormЖорданова нормальная форма матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::jordanForm(A, <All>)
linalg::jordanForm(A) возвращает Жорданову нормальную форму J матричного A.
linalg::jordanForm вычисляет несингулярную матрицу преобразования P и матричный J, таким образом что A = P JP-1 с J = diag (J 1, …, J r) и Иорданские матрицы J 1, …, J r.
Жорданова нормальная форма квадратной матрицы, A по полю F существует, если характеристический полином A разделяет по F в линейные факторы. Если дело обстоит не так для матричного A, затем linalg::jordanForm возвращает FAIL.
Жорданова нормальная форма уникальна до сочетаний Иорданских матриц J 1, …, J r.
Реализованный метод вычисляет собственные значения A. Это возвращает FAIL если это не возможно (см. linalg::eigenvalues).
Звонок компонента A должно быть поле, т.е. область категории Cat::Field.
Жорданова нормальная форма матрицы:
A := Dom::Matrix(Dom::Complex)([[1, 2], [4, 5]])
![]()
следующая матрица:
J := linalg::jordanForm(A)
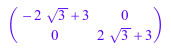
Соответствующая матрица преобразования P может быть получена из результата [J, P] из linalg::jordanForm с опцией All:
P := linalg::jordanForm(A, All)[2]
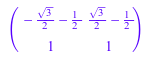
Мы проверяем результат:
map(P * J * P^(-1), radsimp)
![]()
Чтобы получить этот результат, мы должны применить функциональный radsimp к каждому компоненту матрицы, которая возвращена матричным произведением P JP-1.
|
Квадратная матрица области категории |
|
Возвращает список |
Любой матрица того же доменного типа как A, список [J, P] когда опция All дан, или значение FAIL.