`linopt`::`plot_data`

Постройте выполнимую область линейной программы

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

linopt::plot_data([constr, obj, <NonNegative>, <seti>], vars)
linopt::plot_data([constr, obj, <NonNegative>, <All>], vars)
linopt::plot_data([constr, obj, <setn>, <seti>], vars)
linopt::plot_data([constr, obj, <setn>, <All>], vars)

Описание

linopt::plot_data([constr, obj], vars) возвращает графическое описание выполнимой области линейной программы [constr, obj], и линия, вертикальная к вектору целевой функции через угол с максимальным найденным значением целевой функции.

[constr, obj] линейная программа точно с двумя переменными. Проблема имеет ту же структуру как в linopt::maximize. Второй параметр vars задает, какая переменная принадлежит горизонтальной и вертикальной оси.

Примеры

Пример 1

Мы строим выполнимую область данной линейной программы. Здесь допустимые углы линейной программы легко видеть:

k := [{2*x + 2*y >= 4, -2*x + 4*y >= -2, -2*x + y >= -8,
       -2*x + y <= -2, y <= 6}, x + y, NonNegative]:
g := linopt::plot_data(k, [x, y]):
plot(g):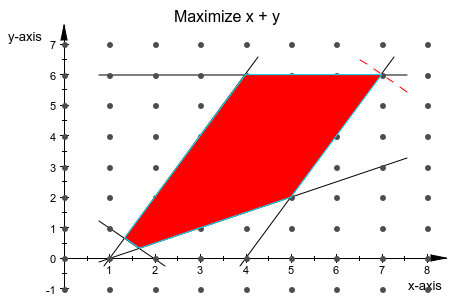

В этом примере нет никакого различия если Опция NonNegative дан для линейной программы или нет:

k := [{2*x + 2*y >= 4, -2*x + 4*y >= -2, -2*x + y >= -8,
       -2*x + y <= -2, y <= 6}, x + y]:
g := linopt::plot_data(k, [x, y]):
plot(g):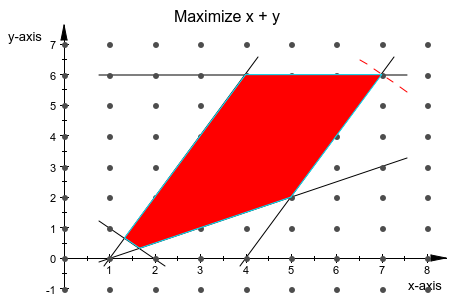

delete k, g:

Пример 2

Теперь мы даем пример, где каждый видит различие, если переменные ограничиваются быть неотрицательными:

k := [{x + y >= -1, x + y <= 3}, x + 2*y]:   
g := linopt::plot_data(k, [x, y]):
plot(g):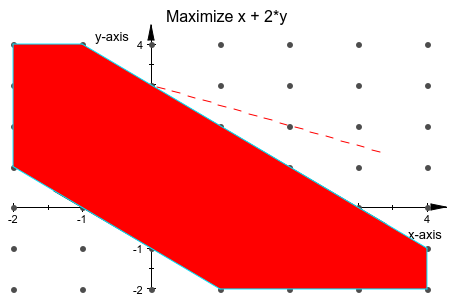

k := [{x + y >= -1, x + y <= 3}, x + 2*y, NonNegative]:
g := linopt::plot_data(k, [x, y]):
plot(g):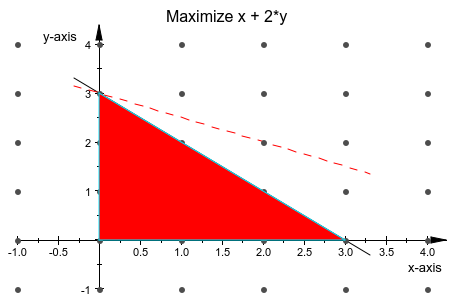

delete k, g:

Параметры

`constr`	Набор или список линейных ограничений
`obj`	Линейное выражение
`seti`	Набор, который содержит идентификаторы, интерпретированные как indeterminates
`setn`	Набор, который содержит идентификаторы, интерпретированные как indeterminates
`vars`	Список, содержащий две переменные линейной программы, описан `constr` и `obj` и существующие опции

Опции

`All`	Все переменные ограничиваются быть целым числом
`NonNegative`	Все переменные ограничиваются быть неотрицательными

Возвращаемые значения

Выражение, описывающее графический объект, который может использоваться plot.

Ссылки

Papadimitriou, Christos H; Steiglitz, Кеннет: комбинаторная оптимизация; алгоритмы и сложность. Prentice Hall, 1982.

Nemhauser, Джордж Л; Wolsey, Лоуренс А: целочисленная и комбинаторная оптимизация. Нью-Йорк, Вайли, 1988.

Салкин, Харви М; Mathur, Kamlesh: основы целочисленного программирования. Северная Голландия, 1989.

Нейман, Клаус; Morlock, Мартин: исследование операций. Мюнхен, Hanser, 1993.

Duerr, Уолтер; Kleibohm, Клаус: Исследование операций; Lineare Modelle und ihre Anwendungen. Мюнхен, Hanser, 1992.

Зуль, Уве Х: MOPS - математическая система оптимизации. Европейский журнал исследования операций 72 (1994) 312-322. Северная Голландия, 1994.

Зуль, Уве Х; Сзыманский, Ральф: обработка суперузла смешанных целочисленных моделей. Бостон, Kluwer академические издатели, 1994.

Документация