`linopt`::`minimize`

Минимизируйте линейную или смешано-целочисленную программу

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

linopt::minimize([constr, obj], <DualPrices>)
linopt::minimize([constr, obj, <NonNegative>, <seti>])
linopt::minimize([constr, obj, <NonNegative>, <All>])
linopt::minimize([constr, obj, <setn>, <seti>])
linopt::minimize([constr, obj, <setn>, <All>])
linopt::minimize([constr, obj, <NonNegative>], DualPrices)
linopt::minimize([constr, obj, <set>], DualPrices)

Описание

linopt::minimize([constr, obj]) возвращает решение линейной или смешано-целочисленной программы, данной ограничениями constr и линейная целевая функция obj который должен быть минимизирован.

Выражение obj линейная целевая функция должна быть минимизирована удовлетворяющая линейным ограничениям constr. Функциональный linopt::minimize возвращает тройное, состоящее из состояния выхода, OPTIMALпустой или UNBOUNDED, набор уравнений, который описывает оптимальное решение заданной линейной программы, которая пуста или зависит от свободной переменной Φ, удовлетворяющий состоянию, и наконец минимальному значению целевой функции, которое может быть любой номером, infinity или линейная функция в Φ.

Состояния OPTIMALпустой или UNBOUNDED имейте следующие значения. OPTIMAL означает, что оптимальное решение для линейной программы было найдено. Если состоянием является EMPTY никакое оптимальное решение не было найдено и если это - UNBOUNDED затем решение не имеет никакой верхней границы.

Если опция NonNegative используется все переменные ограничиваются быть неотрицательными. Если вместо NonNegative набор setn дан затем только переменные из setn ограничиваются быть неотрицательным.

Если опция All используется все переменные ограничиваются быть целыми числами. Если вместо All набор seti дан, затем только переменные из seti ограничиваются быть целыми числами.

Как второй параметр для linopt::minimize опция DualPrices обеспечивается для линейного случая (первый параметр поэтому не должен иметь больше чем трех элементов). Эта опция вызывает выход двойных цен в дополнение к решению-tripel. В этом случае результат linopt::minimize последовательность списка, содержащего решение-tripel и набор, содержащий двойные цены. Смотрите Пример 4.

Примеры

Пример 1

Мы пытаемся решить линейную программу

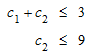
с линейной целевой функцией - c ₁ - c ₂:

linopt::minimize([{c1 + c2 <= 3, c2 <= 9}, -c1 - c2])

Пример 2

Теперь давайте взглянем на линейную программу

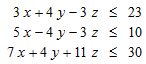
с линейной целевой функцией - x + y + 2 z. Если мы не делаем ограничения на переменные, результат неограничен:

c := [{3*x + 4*y - 3*z <= 23, 5*x - 4*y - 3*z <= 10, 
       7*x + 4*y + 11*z <= 30}, -x + y + 2*z]:
linopt::minimize(c)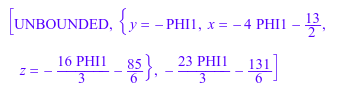

Но если все переменные ограничиваются быть неотрицательными, мы получаем результат. Это также имеет место, если только X и Y ограничиваются быть неотрицательными:

linopt::minimize(append(c, NonNegative));
linopt::minimize(append(c, {x, y}))

delete c:

Пример 3

Следующая линейная программа не имеет решения:

linopt::minimize([{x <= -1, x >= 0}, x])

Пример 4

Выход двойных цен может быть осуществлен с опцией DualPrices:

linopt::minimize([{c1 + c2 <= 3, c2 <= 9}, -c1 - c2],
                 DualPrices)

Параметры

`constr`	Набор или список линейных ограничений
`obj`	Линейное выражение
`seti`	S набор, который содержит идентификаторы, интерпретированные как indeterminates
`setn`	Набор, который содержит идентификаторы, интерпретированные как indeterminates

Опции

`All`	Все переменные ограничиваются быть целым числом
`NonNegative`	Все переменные ограничиваются быть неотрицательными
`DualPrices`	Эта опция только доступна в линейном случае. Это вызывает выход двойных цен в дополнение к решению-tripel.

Возвращаемые значения

Перечислите или последовательность списка и набора, содержащего решение линейной или смешано-целочисленной программы.

Ссылки

Papadimitriou, Christos H; Steiglitz, Кеннет: комбинаторная оптимизация; алгоритмы и сложность. Prentice Hall, 1982.

Nemhauser, Джордж Л; Wolsey, Лоуренс А: целочисленная и комбинаторная оптимизация. Нью-Йорк, Вайли, 1988.

Салкин, Харви М; Mathur, Kamlesh: основы целочисленного программирования. Северная Голландия, 1989.

Нейман, Клаус; Morlock, Мартин: исследование операций. Мюнхен, Hanser, 1993.

Duerr, Уолтер; Kleibohm, Клаус: Исследование операций; Lineare Modelle und ihre Anwendungen. Мюнхен, Hanser, 1992.

Зуль, Уве Х: MOPS - математическая система оптимизации. Европейский журнал исследования операций 72 (1994) 312-322. Северная Голландия, 1994.

Зуль, Уве Х; Сзыманский, Ральф: обработка суперузла смешанных целочисленных моделей. Бостон, Kluwer академические издатели, 1994.

Документация