linopt::Transparent::autostep
Выполните следующий симплексный шаг
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
linopt::Transparent::autostep(tableau)
Описание
linopt::Transparent::autostep(tableau) выполняет следующий шаг симплексного алгоритма. Это - тот же шаг что linopt::Transparent::suggest предложил бы для данной симплексной таблицы tableau.
Обычно linopt::Transparent::autostep возвращает следующую симплексную таблицу. Если вычислением симплексного алгоритма является законченный linopt::Transparent::autostep возвращает набор, содержащий решение данной линейной программы, описанной tableau.
Примеры
Пример 1
Обычная симплексная таблица данной линейной программы создается:
k := [{x + y >= 2}, x, NonNegative]:
t := linopt::Transparent(k)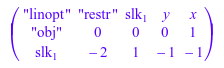
Следующие два шага симплексного алгоритма выполняются для данной симплексной таблицы:
linopt::Transparent::autostep(t); linopt::Transparent::autostep(%)
delete k, t:
Пример 2
Обычная симплексная таблица данной линейной программы создается:
k := [{x + y >= -1, x + y <= 3}, x + 2*y, NonNegative]:
t := linopt::Transparent(k)
Если конец симплексного алгоритма достигнут, linopt::Transparent::autostep возвращает решение данной линейной программы:
linopt::Transparent::suggest(t), linopt::Transparent::autostep(t)
delete k, t:
Параметры
|
Симплексная таблица доменного типа |
Возвращаемые значения
Симплексная таблица доменного типа linopt::Transparent или набор, который содержит решение линейной программы.
Ссылки
Papadimitriou, Christos H; Steiglitz, Кеннет: комбинаторная оптимизация; алгоритмы и сложность. Prentice Hall, 1982.
Nemhauser, Джордж Л; Wolsey, Лоуренс А: целочисленная и комбинаторная оптимизация. Нью-Йорк, Вайли, 1988.
Салкин, Харви М; Mathur, Kamlesh: основы целочисленного программирования. Северная Голландия, 1989.
Нейман, Клаус; Morlock, Мартин: исследование операций. Мюнхен, Hanser, 1993.
Duerr, Уолтер; Kleibohm, Клаус: Исследование операций; Lineare Modelle und ihre Anwendungen. Мюнхен, Hanser, 1992.
Зуль, Уве Х: MOPS - математическая система оптимизации. Европейский журнал исследования операций 72 (1994) 312-322. Северная Голландия, 1994.
Зуль, Уве Х; Сзыманский, Ральф: обработка суперузла смешанных целочисленных моделей. Бостон, Kluwer академические издатели, 1994.