linopt::Transparent::convert
Преобразуйте данную таблицу в структуру, печатаемую на экране
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
linopt::Transparent::convert(tableau)
Описание
linopt::Transparent::convert преобразует tableau в двумерную матрицу, которая соответствует экранной таблице. Можно теперь получить доступ к элементу в i-th строка и j-th столбец симплексной таблицы путем доступа к соответствующему элементу массива.
Внутренне данный tableau из доменного типа linopt::Transparent содержит большую больше информации, чем симплексная таблица, которая распечатана некоторыми функциями linopt библиотека, например, linopt::Transparent::simplex, и который отображается на экране. Кроме того, не возможно получить доступ к элементу в i-th строка и j-th столбец tableau получить соответствующий элемент из симплексной таблицы, которая отображается на экране.
В то время как внутренняя структура tableau не известен структура двумерной матрицы четко определена. Таким образом, это может легко использоваться в собственных процедурах. Смотрите Пример 2.
Примеры
Пример 1
Мы преобразуем симплексную таблицу доменного типа linopt::Transparent в двумерную матрицу:
k := [{x + y >= 2}, x, NonNegative]:
t := linopt::Transparent(k):
a := linopt::Transparent::convert(t):
t, domtype(t);
a, domtype(a)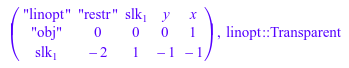
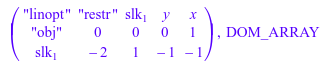
delete a, k, t:
Пример 2
Мы запишем другой симплексный стандартный mysimplex для решения линейной программы. Для этого мы задаем функциональный eigenpivot для нахождения элемента центра данной симплексной таблицы. eigenpivot принимает, что симплексная таблица дана как двумерная матрица.
Вот является процедура eigenpivot, который не закодирован в каждых деталях, например, проверка ошибок не реализована полностью:
eigenpivot := proc(T: DOM_ARRAY)
local i,j,m,n,k,l,mini;
begin
m := op(T,[0,2,2]):
n := op(T,[0,3,2]):
k := 0:
l := 0:
mini := unbesetzt:
for j from 3 to n do
if T[2,j] < 0 then
l := j:
break
end_if:
end_for:
if l=0 then return(OPTIMAL) end_if:
for i from 3 to m do
if T[i,l] > 0 and (mini=unbesetzt or T[i,2]/T[i,l] < mini) then
k := i:
mini := T[k,2]/T[k,l]
end_if
end_for:
if k=0 then return(UNBOUNDED) end_if:
return(T[k,1],T[1,l]):
end_proc:Это - новый симплексный алгоритм mysimplex который использует eigenpivot и некоторая функция от linopt библиотека:
mysimplex := proc(P)
local T;
begin
T := linopt::Transparent(P):
T := linopt::Transparent::phaseI_tableau(T):
piv := eigenpivot(linopt::Transparent::convert(T)):
while piv <> OPTIMAL and piv <> UNBOUNDED do
T := linopt::Transparent::userstep(T,piv):
piv := eigenpivot(linopt::Transparent::convert(T))
end_while:
if piv = UNBOUNDED then
error(" Phase I unbounded ?!?")
end_if:
if T[2,2] <> 0
then return(EMPTY)
end_if:
T := linopt::Transparent::clean_basis(T):
T := linopt::Transparent::phaseII_tableau(T):
piv := eigenpivot(linopt::Transparent::convert(T)):
while piv <> OPTIMAL and piv <> UNBOUNDED do
T := linopt::Transparent::userstep(T,piv):
piv := eigenpivot(linopt::Transparent::convert(T))
end_while:
if piv = OPTIMAL
then return(linopt::Transparent::result(T))
else return(UNBOUNDED)
end_if
end_proc:Мы теперь применяем mysimplex к линейной программе:
k := [{2*x + 2*y >= 4, -2*x + 4*y >= -2, -2*x + y>= -8,
-2*x + y <= -2, y <= 6}, -x - y]:
k := append(k, NonNegative):
mysimplex(k);
delete k, eigenpivot, mysimplex:
Параметры
|
Симплексная таблица доменного типа |
Возвращаемые значения
Двумерная матрица, представляя данную симплексную таблицу tableau.
Ссылки
Papadimitriou, Christos H; Steiglitz, Кеннет: комбинаторная оптимизация; алгоритмы и сложность. Prentice Hall, 1982.
Nemhauser, Джордж Л; Wolsey, Лоуренс А: целочисленная и комбинаторная оптимизация. Нью-Йорк, Вайли, 1988.
Салкин, Харви М; Mathur, Kamlesh: основы целочисленного программирования. Северная Голландия, 1989.
Нейман, Клаус; Morlock, Мартин: исследование операций. Мюнхен, Hanser, 1993.
Duerr, Уолтер; Kleibohm, Клаус: Исследование операций; Lineare Modelle und ihre Anwendungen. Мюнхен, Hanser, 1992.
Зуль, Уве Х: MOPS - математическая система оптимизации. Европейский журнал исследования операций 72 (1994) 312-322. Северная Голландия, 1994.
Зуль, Уве Х; Сзыманский, Ральф: обработка суперузла смешанных целочисленных моделей. Бостон, Kluwer академические издатели, 1994.