ode::scalarEquation
Преобразовывает линейную дифференциальную систему к эквивалентному скалярному линейному дифференциальному уравнению
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
ode::scalarEquation(A, x, y, <Transform>)
Описание
ode::scalarEquation преобразует первый порядок гомогенная линейная дифференциальная система в эквивалентное гомогенное скалярное линейное дифференциальное уравнение с помощью метода циклического вектора.
ode::scalarEquation(A, x, y) возвращает скалярное гомогенное линейное дифференциальное уравнение в y(x) эквивалентный первому порядку гомогенная дифференциальная система
с помощью метода циклического вектора. Если опция Transform дан затем, список возвращен, чей первый элемент является соответствующим дифференциальным уравнением Ly и второй элемент является обратимой матрицей P таким образом, который
сопровождающая матрица, сопоставленная к Ly; следовательно, если Z решение дифференциальной системы
затем, PZ является решением системы
.
Примеры
Пример 1
Мы вычисляем линейное дифференциальное уравнение, эквивалентное следующей дифференциальной системе:
A := matrix( [ [x^2-1,1,0], [0,x^2+5*x+1/3,1], [0,0,2]])
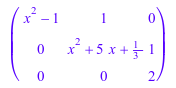
l := ode::scalarEquation(A, x, y, Transform)
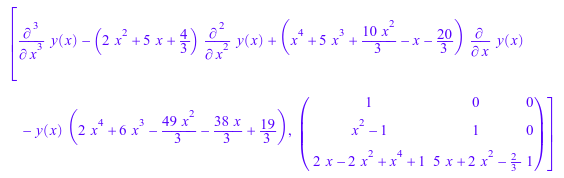
И мы можем проверять это для P=l[2],
сопровождающая матрица, сопоставленная к l[1]:
P := l[2]:
bool( diff(P,x)*P^(-1)+P*A*P^(-1) =
ode::companionSystem(l[1], y(x)) )
Параметры
|
Квадратная матрица типа |
|
Независимая переменная получившегося скалярного дифференциального уравнения. |
|
Зависимая переменная получившегося скалярного дифференциального уравнения. |
Возвращаемые значения
Выражение или список.