pade
Приближение Padé
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
pade(f,x, <[m, n]>) pade(f,x = x0, <[m, n]>)
Описание
pade(f, ...) вычисляет аппроксимирующую функцию Pade выражения f.
Аппроксимирующая функция Pade порядка [m, n] вокруг x = x 0 является рациональным выражением
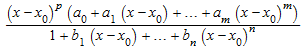
аппроксимация f. Параметры, которые p и a 0 даны ведущим порядком, называют f = a 0 (x - x 0) p + O ((x - x 0) p + 1) последовательного расширения f вокруг x = x 0. Параметры a 1, …, b n выбран таким образом, что последовательное расширение аппроксимирующей функции Pade совпадает с последовательным расширением f к максимальному возможному порядку.
Расширение указывает infinityБесконечность, и complexInfinity не позволены.
Если никакое последовательное расширение f не может быть вычислено, то FAIL возвращен. Обратите внимание на то, что series должен смочь произвести Ряд Тейлора или Ряд Лорана f, т.е. расширение в терминах целочисленных степеней x - x 0 должен существовать.
Примеры
Пример 1
Аппроксимирующая функция Pade является рациональным приближением последовательного расширения:
f := cos(x)/(1 + x): P := pade(f, x, [2, 2])
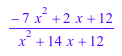
Для большинства выражений ведущего порядка 0 последовательное расширение аппроксимирующей функции Pade совпадает с последовательным расширением выражения через порядок m + n:
S := series(f, x, 6)
Это отличается от расширения аппроксимирующей функции Pade в порядке 5:
series(P, x, 6)
Последовательное расширение может использоваться непосредственно в качестве входа к pade:
pade(S, x, [2, 3]), pade(S, x, [3, 2])
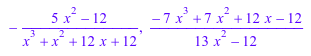
Оба аппроксимирующие функции Pade аппроксимируют f через порядок m + n = 5:
map([%], series, x)
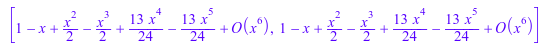
delete f, P, S:
Пример 2
Следующее выражение не имеет расширения Лорана вокруг x = 0:
series(x^(1/3)/(1 - x), x)
Следовательно, pade сбои:
pade(x^(1/3)/(1 - x), x, [3, 2])
Пример 3
Обратите внимание на то, что заданные порядки [m, n] не обязательно совпадает с порядками числителя и знаменателя, если последовательное расширение не запускается с постоянного термина:
pade(x^10*exp(x), x, [2, 2]), pade(x^(-10)*exp(x), x, [2, 2])
Параметры
|
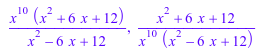
Арифметическое выражение или серия доменного типа |
| |
|
Арифметическое выражение. Если |
|
Список неотрицательных целых чисел, задающих порядок приближения. Значениями по умолчанию является |
Возвращаемые значения
Арифметическое выражение или FAIL.